單相逆變器新型重復-模糊控制方案
由圖2可得,d(z)到e(z)的傳遞函數為:

式中:ω∈[0,π/t],T為采樣周期。
3.2 重復控制器設計
按照重復控制器設計的一般步驟進行設計:
(1)z-N前向通道上串聯的z-N使控制信號延遲一個基波周期輸出,即當前檢測到的誤差信號要到下一個周期才作為控制量的一部分對系統產生調節作用。值得注意的是,z-N也是實現zk所必須的。系統采樣頻率為10 kHz,輸出電壓頻率為50 Hz,因此N=200。
(2)Q(z)理想的重復控制系統中,Q(z)=1,但內模的N個處于單位圓上的極點使系統處于臨界穩定狀態。為增強系統穩定性,Q(z)一般取略小于1的正常數或低通濾波器,此處取Q(z)=0.95。
(3)S(z) S(z)是根據被控對象特性而設計的,其作用是將被控對象中的低頻段增益校正為1,提高系統抗干擾能力,一般由零相移陷波器和二階低通濾波器串聯組成,分別用于消除逆變器高諧振峰和提供高頻衰減能力。此處設計零相移陷波器S1(z)=(z5+2+z-5)/4,二階低通濾波器S2(z)=(0.1302z+0.094 4)/(z2-1.1582z+0.383)。
(4)zk zk用于補償S(z)和被控對象引入的相位滯后,使S(z)P(z)在中低頻段接近零相移,k為超前步長,此處k=4。
(5)Kr Kr用于改變重復控制器內模輸出量的幅值,其值越小,系統穩定裕度越大,但誤差收斂速度有所下降;反之,誤差收斂速度越快,但系統穩定性更差。經實驗反復調試。取Kr=0.8。將上述參數代入式(6)可知,重復控制系統是穩定的。
4 系統復合控制
重復控制雖能保證系統具有較高穩態精度,但重復控制對擾動的調節滯后一個基波周期,即從發現擾動到實施控制,需一個基波周期的時間間隔,當系統承受階躍信號或突加突卸負載時,系統幾乎處于開環狀態,重復控制器不起任何作用,故其動態響應特性較差。為滿足逆變器對動態性能和穩態精度的要求,提出將重復控制與模糊自整定比例控制相結合的控制方案,如圖3所示。本文引用地址:http://www.104case.com/article/159488.htm

利用重復控制改善系統穩態性能,而對參數變化具有較強適應性的模糊自整定比例控制則用于改善系統動態特性。并在重復控制器前饋通路上增加前饋系數km。來消除嵌入式重復控制系統引起的輸出電壓在第一個基波周期的超調;重復控制器與模糊控制器為并聯結構,二者采用分段控制方式。系統運行時,模態選擇開關不斷檢測電壓誤差,在系統啟動或遇到突加擾動時,誤差絕對值大于設定閾值,模態選擇開關切換到模糊控制,保證系統有較快動態響應速度;當誤差絕對值小于設定閾值時,系統已進入穩態,模態選擇開關切換到重復控制,保證系統有較高穩態精度。
傳統模糊控制器多以誤差e和誤差變化率ec作為輸入,經模糊化后在一定模糊規則下進行模糊推理,再查詢模糊矩陣表得到相應控制量。顯然,模糊控制器輸入量越多,模糊規則越細,實現起來就越復雜。文獻提出了一種單輸入模糊控制器(SIFLC)設計方法,可將二維輸入模糊規則表簡化為一維,且能達到與原控制器相同的控制效果。在文獻基礎上,采用圖4所示的改進型單輸入模糊控制器對比例因子kp進行在線自整定。
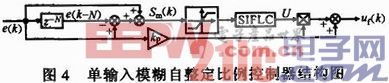
圖5示出改進的單輸入模糊子集的隸屬度函數。模糊輸入變量S和輸出變量U的論域劃分為7個模糊子集:負大(NB)、負中(NM)、負小(NS)、零(Z)、正小(PS)、正中(PM)、正大(PB),論域范圍為[-1,1],隸屬函數為等腰三角形。改進型單輸入模糊控制規則如表1所示。二維輸入轉換到單輸入可通過S=e(i)+ec(j),i,j=1,2,…,7實現。





評論