雷達成像近似二維模型及其超分辨算法
加入技術交流群
從式(12)可以看出：
是Zk歸一化的二維離散傅里葉變換在{ωk,
k}處的值，所以只要得到估計值{
k,
k,
k,
k}，即可通過2D-FFT獲得k.
將估計值k代入式(11)后，估計值{k,k,k,k}可由下式尋優得到：
(13)
由上式可見，對于固定的{μk,vk}取值,估計值{k,k}為歸一化的周期圖|aHM(ωk)Zkb*N(k)|2/(MN)主峰處的二維頻率值.這樣，式(13)的優化問題歸結為：在(μk,vk)平面上可能的取值范圍內尋找一點{k,k}，在該點處周期圖|aHM(ωk)Zkb*N(k)|2/(MN)的主峰值比其余各點處的主峰值都大.所以，我們通過上述二維尋優獲得{μk,vk}的估計值{k,k}，再由式(13)得到{ωk,k}的估計值{k,k}.
實際中，為了加快運算速度，二維(μk,vk)平面的尋優可以用Matlab中的函數Fmin()實現.
在做了以上的準備工作以后，基于推廣的RELAX算法的參量估計步驟如下：
第一步：假設信號數K=1,分別利用式(13)和式(12)計算
1.
第二步(2)：假設信號數K=2，首先將第一步計算所得到的1代入式(8)求出Y2，再利用式(13)和式(12)計算2；將計算的2代入式(8)求出Y1，然后利用式(13)和式(12)重新計算1，這個過程反復疊代，直至收斂.
第三步:假設信號數K=3,首先將第二步計算所得到的1和2代入式(8)求出Y3，再利用式(13)和式(12)計算3；將計算的3和2代入式(8)求出Y1，然后利用式(13)和式(12)重新計算1；將計算的1和3代入式(8)求出Y2，然后利用式(13)和式(12)重新計算2，這個過程反復疊代，直至收斂.
剩余步驟：令K=K+1,上述步驟持續進行，直到K等于待估計信號數.
上述過程中的收斂判據與RELAX算法的收斂判據相同，即比較代價函數C1在兩次疊代過程中的變化值，如果這個變換值小于某個值，如ε=10-3，則認為過程收斂.
四、數值模擬
1.算法參數估計性能模擬
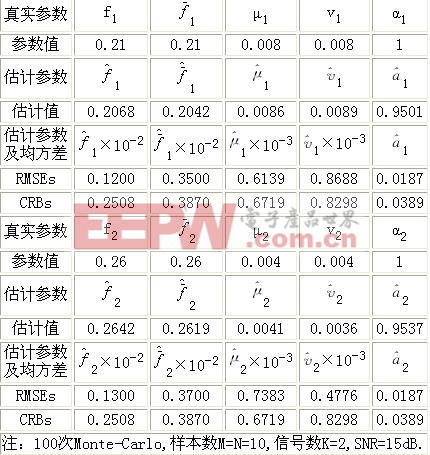
模擬數據由式（5）產生，M=10,N=10，信號數K=2.信號參數和實驗條件如表1所示,為復高斯白噪聲.注意兩信號的頻率差小于FFT的分辨率Δf=Δω/(2π)=0.1.表1給出了信號參數估計均方根誤差的統計結果及相應情形時的C-R界，可見，估計均方根誤差與CR界十分接近.另外表中還給出了估計均值，與真實值也非常接近.
表1 二維信號的參數估計、CRB及與均方根差的比較
評論