針對語音信號的低功耗數字接收機解調方案

　　的實部和虛部均為正。所以，帶通濾波器的系數有這樣的特點：實部偶對稱，虛部奇對稱。

　　3 解調方案二

　　還是以解調上邊帶為例，先搬移待解調信號的頻譜，再做低通濾波，最后又將信號的頻譜搬移回來，如圖7所示。這種方案濾波器的設計思路簡單，但要對信號進行兩次頻譜搬移。

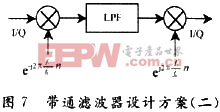
　　LPF與方案一中所設計的低通濾波器相同。如圖8所示，信號被搬至零中頻處。

　　4兩種方案的比較

　　方案一中，帶通濾波器在一個時鐘周期內進行如下的計算：

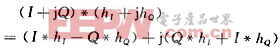
　　其中*表示卷積運算，下同。這表示要做4N次乘加運算，考慮到對稱性只需要2N次乘加運算。

　　如果信號不是獨立邊帶的，上邊帶信號解調所用的帶通濾波器的系數與下邊帶信號解調所用的帶通濾波器的系數是共軛關系，即hUSB(n)=hLSB*(n)，則另外一個邊帶的濾波計算為：

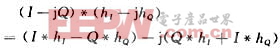
　　其結果與前面的成共軛關系，因此，只要得到其中一個邊帶的實數部分即可得到解調結果。這樣只需要N次乘加運算。

　　如果是獨立邊帶的，上下邊帶的共軛關系不存在，則解調其中一個邊帶需要2N次乘加運算，上下邊帶解調共需要4N次乘加運算。

　　方案二中，低通濾波器在一個時鐘周期內進行如下的計算：

　　這表示要做2N次乘加運算，考慮到對稱性只需要N次乘加運算。

　　如果信號不是獨立邊帶的，那么同方案一，只需要N/2次乘加運算。如果信號是獨立邊帶的那就上下邊帶解調共需要2N次乘加運算。

　　另外兩次經過NCO的運算在一個時鐘周期內共需要8次乘加運算。

　　綜合來說，就運算開銷方面而言方案二要優于方案一。