基于EEMD的信號處理方法分析和實現

信號處理中，頻率是信號最重要的表示。傳統的傅里葉變換分析方法并不能分析出信號的某一頻率在甚么時刻出現，為此產生了能同時在時間和頻率上表示信號密度和強度的時頻分析，如短時傅里葉變換和小波變換等，但其基本思想都是根據傅里葉分析理論，對非線性非平穩信號的分析能力不足，受限于Heisenberg不確定原理。HHT ( Hilbert Huang Transform)是由N. E.Huang 等人在1998 年提出的一種嶄新的時頻分析方法，能夠對非線性非平穩的信號進行分析，同時具有良好自適應性的特點。其本質是對信號進行平穩化處理，將具有不同時間尺度的信號逐級分解開來。

　　HHT 方法在各領域已得到了廣泛應用，但依然存在一些不足，例如易產生虛假分量和模態混疊等。針對傳統經驗模式( Empirical Mode Decomposit iON，EMD)分解方法所導致的模態混疊現象，法國以Flandrin 為首的EMD 算法研究小組和Huang 本人的研究小組通過對EMD 分解白噪聲結果統計特性的大量研究，提出通過加噪聲輔助分析( NA DA ) 的EEMD ( EnsembleEmpirical Mode Decomposition) 方法，將白噪聲加入信號來補充一些缺失的尺度，在信號分解中具有良好的表現。

　　EEMD仿真系統的實現利用了Matlab 平臺，通過GUI 控件實現了系統設計，能直觀方便地進行比較分析，驗證了EEMD 在抗混疊方面較原有方法的改進。

　　1 經驗模式分解( EMD) 和IMF

　　HHT 方法包含兩個主要步驟:

　　( 1) 對原始數據進行經驗模式分解( EMD) ，把數據分解為滿足Hilbert 變換要求的n 階本征模式函數( IMF) 和殘余函數之和。

　　( 2) 對每一階IMF 進行Hilbert 變換，得到瞬時頻率，從而求得時頻圖。

　　函數必須關于時間軸局部對稱，且其過零點與極值點個數相同。此類函數被稱為固有模態函數( Int rinsicMode Function，IMF) 。

　　經驗模式分解方法能把非平穩、非線性信號分解成一組穩態和線性的序列集，即本征模式函數。根據Huang 的定義，每一階的IMF 應滿足兩個條件:

　　( 1) 數據的極值點和過零點交替出現，且數目相等或最多相差一個任何點上；

　　( 2) 在任何點上，有局部最大值和局部最小值定義的包絡的均值必須是零。

　　其篩選算法如下:

　　( 1) 對于輸入信號x ( t) ，確定x ( t) 所有極值點。

　　( 2) 用三次樣條函數對極大點和極小點分別進行擬合得到x ( t) 的上下包絡線。

　　( 3) 用原始數據序列減去上下包絡線的均值。

　　平均曲線：

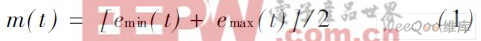
　　細節信號：

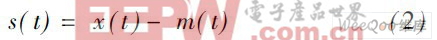
　　( 4) 通常s( t ) 還不滿足IMF 的條件，需重復進行以上步驟，進行迭代處理，H uang 給出的迭代停止準則為：

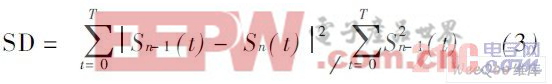
　　SD 是篩選門限值，一般取值為0. 2~ 0. 3，若計算SD 小于這個門限值，篩選迭代將會結束。

　　經過n 次迭代滿足停止準則后得到的sn ( t) 即為有效IMF，剩余信號則進入下一輪篩選過程。

　　經過多次篩選后，原始數據序列被分解為一組IMF 分量和一個殘余量，得到的IMF 都是平穩的，通過Hilbert 變換得到的結果能夠很好地分析非線性非平穩的信號。

　　2 傳統EMD 的不足與缺陷

　　當信號的時間尺度存在跳躍性變化時，對信號進行EMD 分解，會出現一個IMF 分量包含不同時間尺度特征成分的情況，稱之為模態混疊。

　　模態混疊的出現一方面和EMD 的算法有關，另一方面也受原始信號頻率特征的影響。

　　Huang 曾經提出了中斷檢測的方法來解決模態混疊現象，即直接對結果進行觀察，如果出現混疊則重新分解，這種方法需要人為后驗判斷。

　　重慶大學的譚善文提出了多分辨率的EMD 思想，對每一個IMF 規定一個尺度范圍來解決模態混疊，但是這種方法犧牲了EMD 良好的自適應性。