基于DCM模式的Buck直流變換器分動態相量法析

　　摘要：針對工作在DCM模式下的Buck直流變換器這個離散的、時變的、非線性系統，引入虛擬開關函數將一個開關周期中的三種電路拓撲統一到一組狀態空間方程中。采用動態相量法時，合理地選擇了模型中的諧波分量，討論了虛擬開關占空比的取值，建立了其非線性、大信號、時不變模型。仿真結果表明，動態相量模型非常接近于時域模型，為設計基于大信號模型的性能優越控制器提供理論依據。

　　引言

　　動態相量法基于頻率分解的思想，希望以傅里葉級數中極少量的系數來近似原始時域波形，并以這些時變的復相量為狀態變量，來獲得系統化的狀態空間模型。它已被用于高壓直流輸電HVDC、TCSC、有源濾波器、電力電子變換器等系統建模分析中^[1.2]。

　　對于電力電子變換器這個離散的、時變的、非線性系統，在采用動態向量法建模時，通常是引入開關函數，將其不同開關狀態對應的電路拓撲統一到一組時域狀態空間方程中。再作出相應變量的復相量，得到擴大階數的動態相量模型。選擇的變量多為電感的電流和電容的電壓，通常保留其傅里葉系數的直流和基頻分量。對于直流變換器，電感電流存在著CCM(Continuous Conduction Mode)和DCM(Discontinuous Conduction Mode)工作模式。在CCM工作模式下，采用動態相量法建模時能用一個開關函數將一個開關周期中兩種電路拓撲統一到一組時域狀態空間方程中去。由于CCM工作模式中電感電流連續，保留其傅里葉系數的直流和基頻分量可以近似擬合原始時域曲線。但對于DCM工作模式下，一個開關函數無法將一個開關周期中三種電路拓撲統一到一組狀態空間方程中，再者電感電流斷續，其傅里葉級數頻譜豐富，僅用其直流分量、基頻分量較難近似擬合原時域曲線。

　　為了在DCM工作模式下應用動態相量法對系統進行建模分析，本文以Buck直流變換器為例，在建模時引入虛擬開關函數將一個開關周期中的三種電路拓撲統一到一組方程中。同時為保證模型的準確性，動態相量模型中保留傅里葉級數中的直流量、基頻分量和二次分量，建立了Buck直流變換器DCM工作模式下的非線性、大信號、時不變模型。并給出了該模型的仿真結果。

　　動態相量法

　　在時域中x(τ)在任一區間 中的時變傅里葉級數可表示為^[3]：

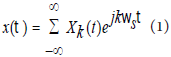
　　式中ω_s=2π/T，X_k(t)是時變傅里葉系數，在動態相量法中定義為“相量”。不同次數的相量，可有下式得到：

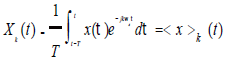       (2)

　　式中X_k(t)是時間的函數，研究的窗(寬度為T)在x(τ)上滑動時，相量就會改變。抓住級數中重要的項，將這些相量作為狀態變量，得到系統狀態空間模型。

　　應用動態相量法有兩個重要特性為：

　　(1)動態向量的微分特性
　　對于第k階傅里葉系數，其微分形式滿足：

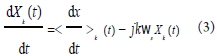
　　(2)相量乘積特性
　　兩個時域變量乘積的動態相量等于每個變量所對應的動態向量的離散卷積為：

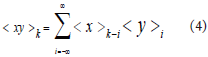
　　Buck直流變換器的動態向量法建模

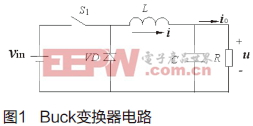
　　Buck變換器電路拓撲

　　Buck變換器電路拓撲如圖1所示，v_in為直流輸入電壓，S₁為開關，u為輸出電壓，i為電感L的電流。建模時做如下假定：認為S₁為理想開關，VD為理想二極管;忽略電感和電容的內阻。由于變換器工作在DCM模式下，在一個開關周期內，電路有三種拓撲結構如圖2所示。開關S₁對應的開關函數q₁波形及電感電流i的波形如圖3所示。當S₁閉合時q₁(t)=1，當S₁斷開時q₁(t)=0。設電感釋放磁場能的時間為d₂T，T為開關周期^[4]。