「技術文章」用蒙特卡羅分析做電源設計

在電子模擬中，元件值總是被認為是固定的。有時設計者想改變這些值來嘗試測試不同的電路行為。其他時候，有必要考慮到相同的值可能會發生變化，因為并非每個電子元件都是理想的。市場上有許多相同電子元件的例子，但在給定公差范圍內具有不同的值。讓我們看看如何使用蒙特卡羅分析來模擬這些值的變化。

此過程執行大量模擬，其中每個組件的值連續隨機變化。他們試圖遵循一個非常自然和隨機的分布。

中的圖表圖1顯示了一個典型的RC電路，其中電容器根據時間常數在一個時間內充電。準確地說，在RC秒后，電壓達到電源電壓的63%。在這種情況下，電容器上的電壓在1000*100E-6秒后為6.32V。

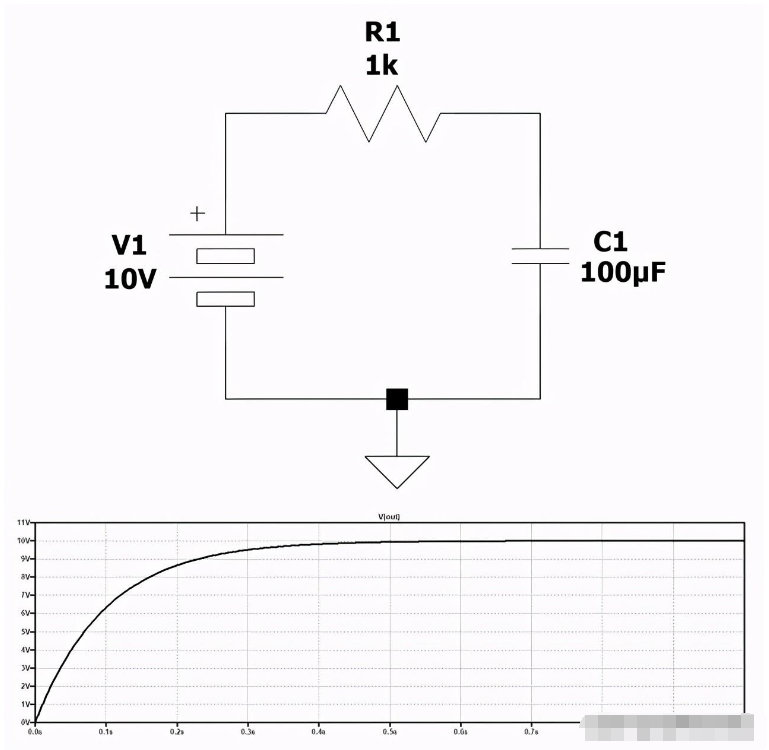
圖1：典型的RC電路

在這個示例方案中，我們假設所有組件的值都是理想的，即：

• 電源電壓V1為10V；

• 電阻器R1為1000歐姆；

• 電容器C1的容量為100微法拉。

由于所有的成分都有理想值，所以即使生成的圖形也是理想的，并且沒有考慮到可能的異常或變化。市場上提供的電阻公差為1%、5%、10%等。即使是電容器，其特性也可能偏離板數據，公差在20%或更多。由于各種原因，蓄電池電壓可能會下降或升高。由于所有這些原因，設計者需要獲得一個“更真實”的圖形，該圖考慮到所用組件值的實際變化，從而使模擬行為更接近真實系統的行為。這就是為什么我們真的希望組件的值不是理想的而是真實的，公差如下：

• 電池V1:10 V，公差2%；

• 電阻器R1:1000歐姆，公差10%；

• 電容器C1:100微法拉，公差25%。

這意味著，在現實中，所使用的電子元件可以假定以下數值范圍：

• 電池V1：電壓在9.8V到10.2之間；

• 電阻器R1:900歐姆至1100歐姆之間的歐姆值；

• 電容器C1：容量在75微法拉和125微法拉之間。

這些變化顯然是同時發生的。理論上，組合的可能值是無限的，但設計者需要觀察電容器電荷圖，在公差規定的自然范圍內盡可能多地變化。功能：

mc（值，公差）

隨機生成x*（1Y）和x*（1-y）之間的隨機值，在公差范圍內指定，具有均勻分布。LTspice接線圖中包含的指南如下：

.param Voltage = mc (10.2 / 100)

.param Resistance = mc (1000,10 / 100)

.param Capacitance = mc (100u, 25/100)

步驟參數模擬1 100 1

測量變壓器電池參數電壓

測量傳輸參數電阻

測量變壓器電容參數

.meas TRAN RC參數電阻*電容

方案的模擬（如所示圖2)表演了一百次。它為每個組件生成100個不同的值。建議您仔細觀察圖表、組件值和指令，以便深入了解程序并能夠繼續閱讀本文。正如你這次看到的，這個圖包含了幾個曲線，對應于電容器上電壓的增加，有100個不同的分量值。執行的模擬越多，最終曲線就越真實，請記住，模擬時間與執行的步數成比例增加。有時，如果電路非常復雜并且由許多元件組成，模擬器需要很長時間來進行數學計算。

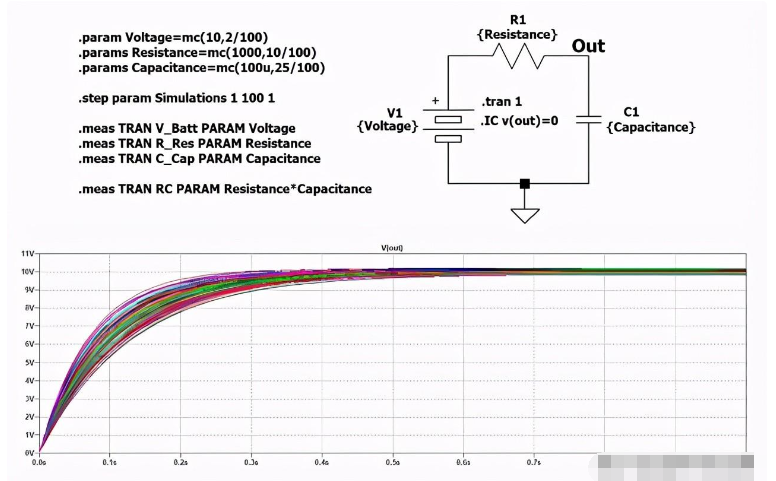
圖2：帶有蒙特卡羅模擬指令的RC電路接線圖和電容器上的電壓圖

在下表中，您將發現程序產生的100個電壓、電阻和容量的一些值。顯然，這些都是由軟件生成的隨機值，因此，對于進一步的模擬，它們總是不同的。

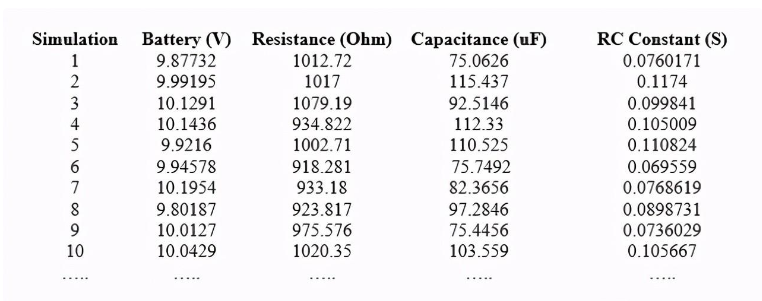
以下結果顯示了隨機生成的數量的最小值和最大值，參考了100個模擬：

• 電池V1產生的最小蒙特卡羅電壓：9.80065 V產生的最大蒙特卡羅電壓：10.1999伏

• 電阻器R1最小蒙特卡羅歐姆值：901.75歐姆最大蒙特卡羅歐姆值：1099.36歐姆

• 電容器C1最小蒙特卡羅容量：75.0626 uF最大蒙特卡羅容量：124759 uF

• 時間常數RC最小“t”：0.069559秒最大“t”：0.13325秒

在圖3我們可以在電容器上的電壓曲線圖中看到發生了什么，精確地說是在0.069559秒到0.13325秒之間的時間間隔內，用100個蒙特卡羅模擬進行的。元件在不同環境下的變化使我們了解它們如何影響和改變電子電路的行為及其時序。

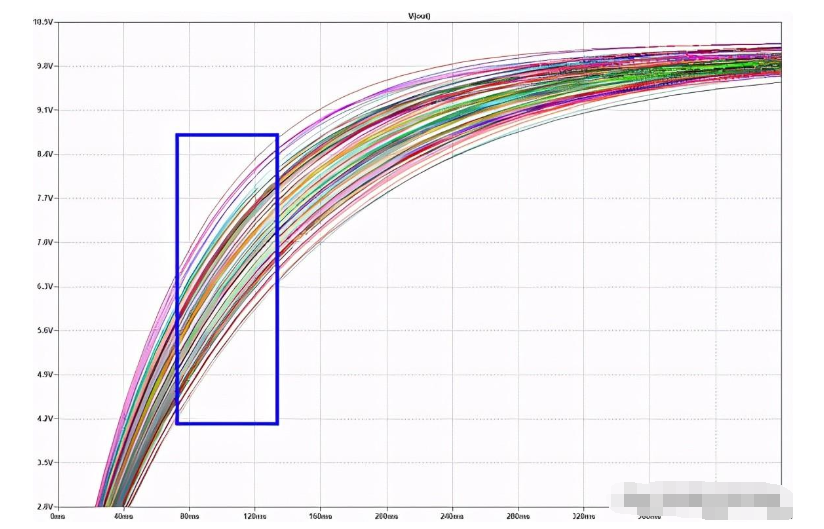
圖3：用軟件生成的組件值觀察時間常數

在DC/DC變換器中，最重要的功率損耗是由開關轉換引起的。損耗與開關頻率和寄生電容值成正比。這個SiC MOSFET用于切換的s是最重要的，尤其是Rds（ON）參數和切換速度。中所示的升壓轉換器圖4由以下組件組成：

• 13 V發電機V1，可以是電池或光伏板；

• mH2電感器；

• UF3C065080T3S-sicmosfet；

• 功率肖特基二極管；

• 50歐姆負載

此升壓轉換器以開關頻率f=10 kHz運行。

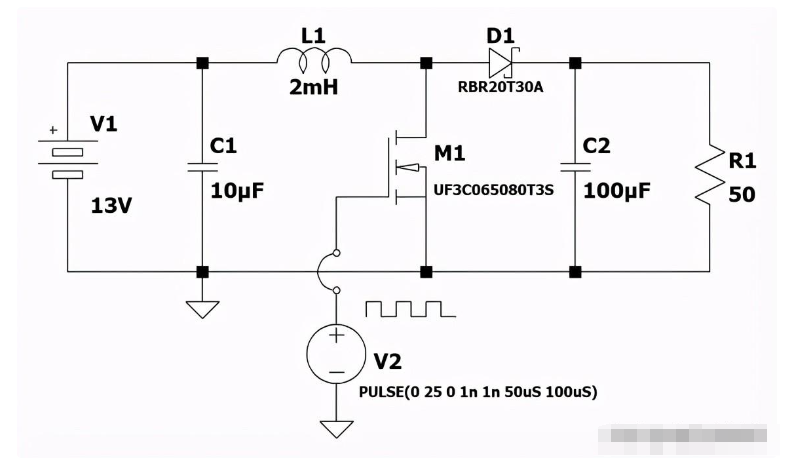
圖4:13V到26V DC/DC升壓變換器

部件不是真實的，因此我們可以很容易地接受以下公差：

• V1:/-20%

• C1:/-25%

• L1:/-15%

• C2:/-25%

• R1:/-5%

• 溫度：/-30%

圖中包含的SPICE指令和命令如下：

.param Voltage = mc (13.20 / 100)

.param Cap1 = mc (10u, 25/100)

.param Induct = mc (2m, 15/100)

.param Cap2 = mc (100u, 25/100)

.param Load = mc (50.5 / 100)

.param T = mc (27.30 / 100)

.溫度{T}

.步驟參數模擬1 10 1

測量變壓器電池參數電壓

.meas TRAN capator1參數Cap1

.meas trans Inductor參數感應

.meas TRAN captor2參數Cap2

.meas TRAN電阻器參數負載

測量變壓器溫度參數

我們只提供了10代人的全面的模擬值。請記住，模擬次數越多，最終結果越好。在圖5我們可以看到十種不同的操作條件的模擬，持續了大約15分鐘，并在1.3gb的硬盤上生成了一個臨時文件。下表顯示了蒙特卡羅方法生成的組件值，在任何情況下都在聲明的公差范圍內。

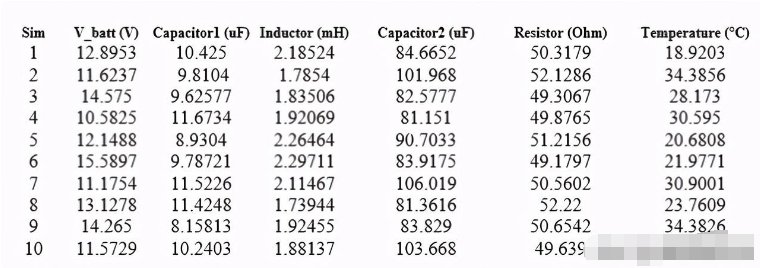
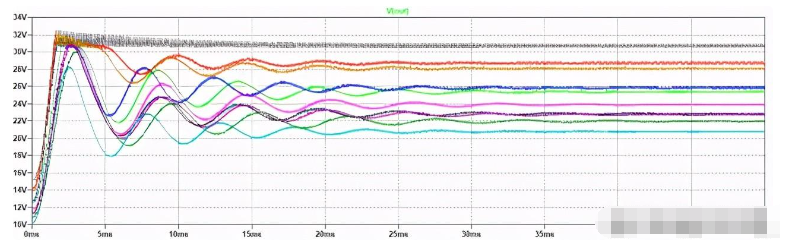
圖5：升壓變換器行為的蒙特卡羅模擬，顯示了負載上的電壓取決于電子元件的不同值

通過適當的操作，還可以隨機改變其他參數，如Sic MOSFET的Rds（ON）和工作頻率等。計算機電子模擬通常是完美和無誤差的，特別是在指定唯一和準確的值時。用蒙特卡羅方法增加了測試的實因子，使電路的行為更接近真實。使用這種方法，當電子元件的值處于允許的最小值和最大值時，可以觀察系統的行為。