搞技術，不要只會調參數

大家好，我是小麥。

以前做控制相關的項目，總會遇到PID的算法，在工程領域，這無疑是簡單，實用，有效的一個算法。

只需要調整比例，積分，微分的參數，就能達到比較好的控制效果。

但是這其中，我們最好是知其然，知其所以然。

控制其實是一門比較綜合的學科，有時候感覺它是批著控制外衣的數學，下面是國外大佬Brian Douglas總結的圖解控制理論，如下圖所示；

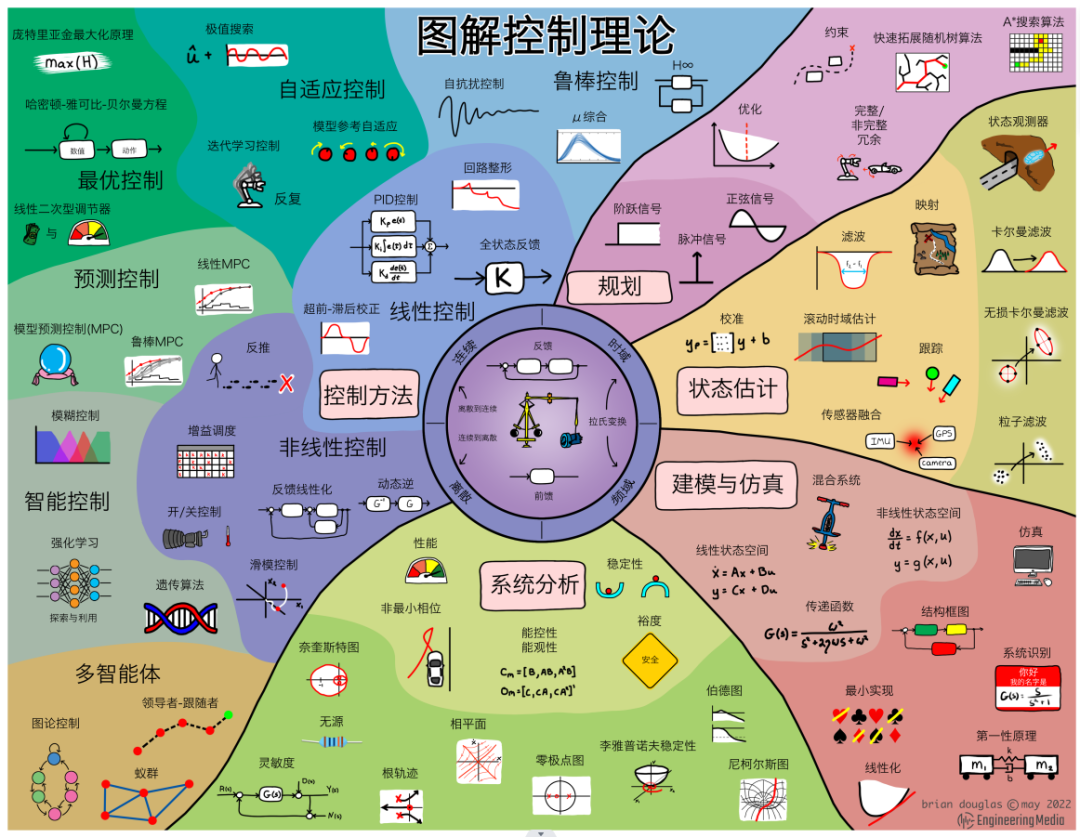
From Brian Douglas

控制理論是龐然大物，后來我在B站看到DR_CAN的視頻，中文講解，由淺入深，受益匪淺。

所以這里給大家強烈安利DR_CAN的新書《控制之美（卷1）——控制理論從傳遞函數到狀態空間》，配合視頻看，效果不錯。老規矩，文末送書

解決一個控制系統的問題，可以分為三個步驟。

第一步需要對所研究的對象進行系統分析，建立數學模型，有可能是熱力學，動力學，流體，甚至是生態或者經濟學模型。

第二步是在這個數學模型的基礎上進行控制器的設計。可以應用到不同的控制手段和方法。

最后一步就是測試。

這里面需要有測試模型的搭建，實驗設計，當然還會涉及到一些數據處理。

同時實驗設備在做出來之后，也需要把實驗結果與建模進行比較，對數學模型進行驗證和不斷地更新。

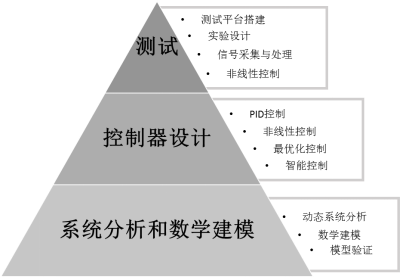
如圖所示，動態系統的分析和數學建模是分析控制系統的基礎，后續的工作都將在這一個基礎上完成。

在這里我們用兩種不同的方法介紹動態系統的分析與數學建模。

首先重點討論經典控制理論的建模方法，即采用拉普拉斯變換和傳遞函數的辦法來描述系統。

從動態系統的本質入手，重點解釋如下三個問題：

• 動態系統的本質是什么？

• 為什么在經典控制中引入拉普拉斯變換，意義和好處在哪？

• 傳遞函數的涵義和控制系統設計的基本概念。

對于動態系統來說，系統狀態變量會隨著時間變化。

對動態系統進行數學建模就是用等式去描述系統狀態變量的變化規律。

本文中，如果不另外說明，研究的對象是線性常系數微分方程，對應的系統就是線性時不變系統

從嚴格意義上來講，時不變系統是不存在的，因為“人不能兩次踏進同一條河流”，而在大部分工程情況下，可以把問題近似簡化為時不變系統。

就是說在系統分析的時間區間內，系統的參數是恒定的。對于非線性的系統，一般可以在系統的平衡點附近做線性化處理。不可以近似為線性時不變的系統不在本書的討論范圍之內。

對于一個線性時不變系統而言，可以通過一個沖激響應得到系統的全部特性。而系統的輸入與輸出是卷積的關系。用簡單直觀的語言來說就是系統的輸入會對未來一段時間之內的系統輸出產生影響。

可以做一個簡單的比喻；

• 向水中扔一枚石子，會產生漣漪。

• 如果在第一次漣漪消失之前，又向水中扔了另一顆石子，那么這兩次的漣漪就會疊加。

• 這其中，扔石子這個動作就是系統的輸入，水面就是系統本身，而產生的漣漪就是系統的輸出。

這說明，某一個時刻的漣漪，是前面幾次石子入水后的疊加的效果。

這個疊加用數學語言來表示就是卷積，下面通過一個例子來推導一下卷積的公式，一步步揭開卷積的面紗，從而了解動態系統的本質。