如何利用電路的“時間常數”預判響應？

“時間常數”哪學來的？

     “電路”/“信號與系統”/“自動控制原理”，多次揭示一階系統的運行規律，其中τ(tao)就是時間常數time constant。電路中，RC串聯的零狀態響應是典型的一階電路，τ=RC。

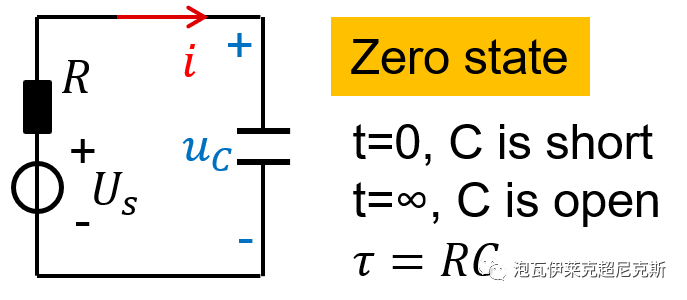
    若u(t)為單位階躍輸入，輸出y(t)經過3-5個τ的滯后才可近似認為進入了穩態，達到靜態增益k。

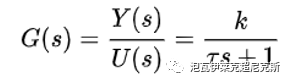
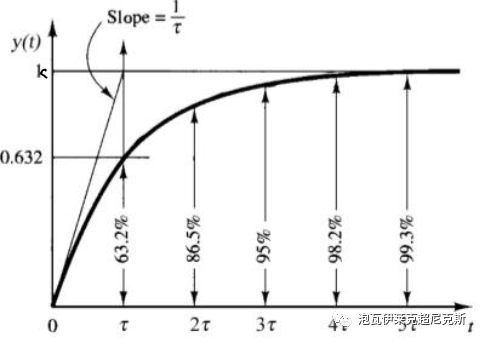
    簡言之，“時間常數”只針對一階系統，廣義上的時間常數或可針對主導極點為一階形式的，類一階的高階系統。直觀地說，它代表了系統對抗外界變化，保持原狀的抵抗能力（慣性）。

    那么，從穩態來看，只要我身為舔狗等女神足夠久，一階環節的時間常數并不會對直流輸入產生影響。

直流書上都有，交流呢？

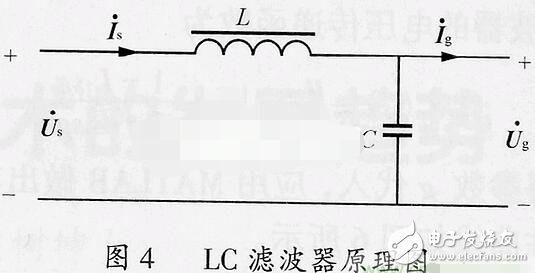
    實際工程的采樣環節中，除了直流信號，我們常遇到交流信號（或含交流信號）的調理與高頻噪聲濾除，最簡單且典型的，即采用一階濾波電路實現。

    濾掉高頻噪聲很簡單，但我們也應該關心，經過時間常數τ的一階濾波，正弦輸入基波的穩態響應，有沒有可能被濾過頭？

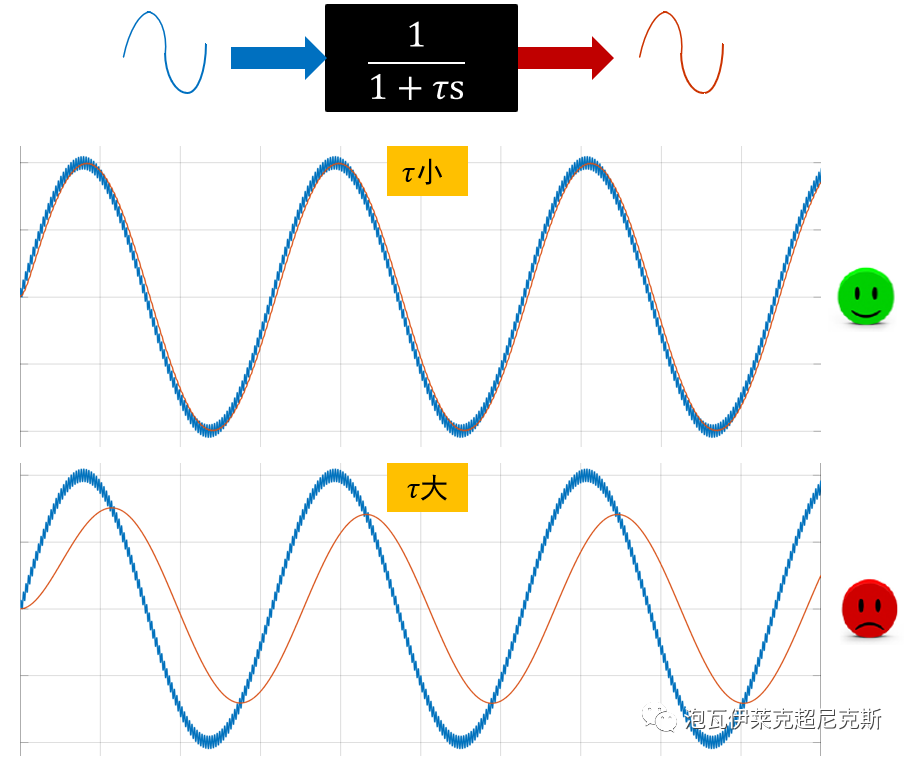
    從用戶友好+小白實用的角度出發，必然是直接從時域得到結論。

•   已知輸入波形周期100us，一階濾波器的時間常數取多少us才可以不失真（幅度，相位）？

•   系統穩定后，輸入輸出兩個正弦的基波，在時域上有多少延遲？

  
  

    不必每次都理論計算/仿真，而能秒答這兩個問題，加速調試和設計過程，是本文撰寫的初衷。

    為了盡可能量化，聯系理論工具：正弦穩態響應→波特圖。

    一階系統波特圖和漸近線如下，轉折頻率為藍色線fc，輸入的ac信號基波頻率為綠色線fac。

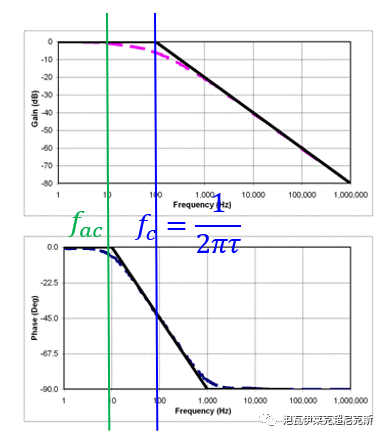
    由圖可知，為了幾乎不產生衰減和相移的失真，放在轉折頻率1/10以下，fac<fc/10。

    我們就把fac放在fc/10的地方，為了找出時間常數和交流信號，在時域的直接關系，列表如下：

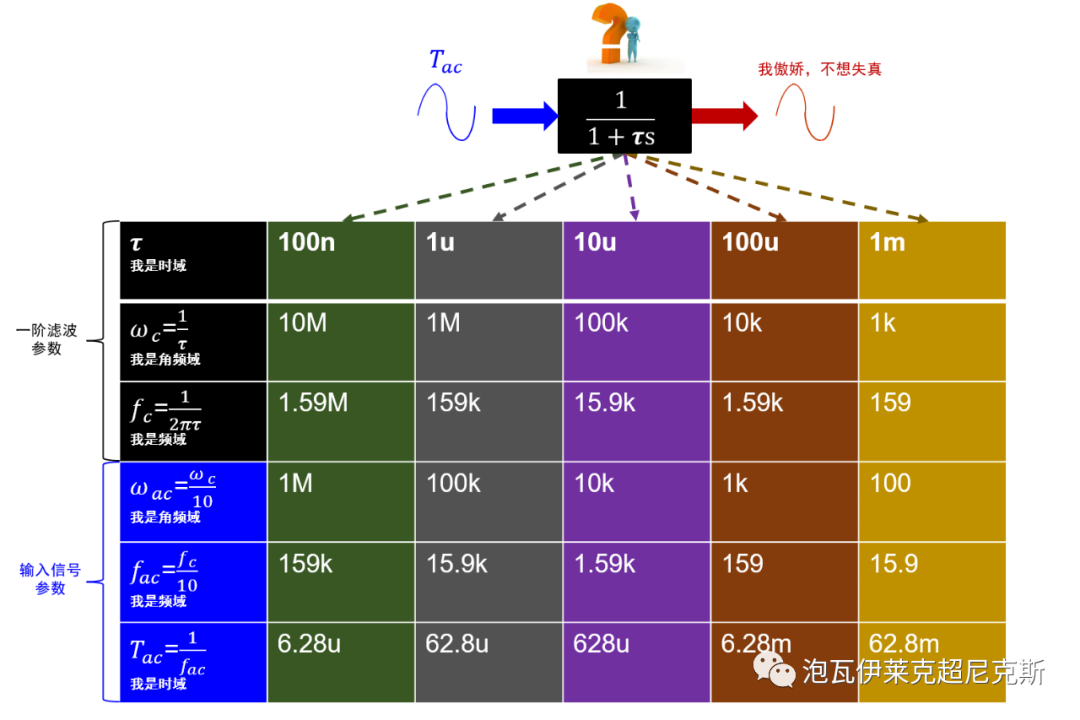
     結論：頻域幅度和相位的不失真，即時域上幅度縮小和時間延遲近似忽略的情況下，在時域上需求的倍數關系高達62.8，也就是說，針對100us周期的輸入信號，濾波器時間常數不要超過1.6us。

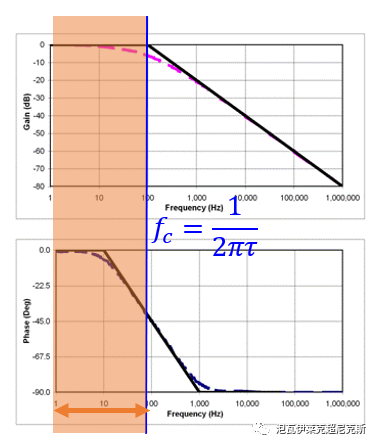
    那么，為了研究時域延遲，如果讓輸入信號頻率fac在fc之下自由移動，（上圖中橙色區域），即周期低于20pi*τ，相移會有負的0°-45°之多，對應的時域呢？

    一階系統相位表達式如下，橙色區域恰對應自變量2pi*f*τ的范圍在[0，1]。

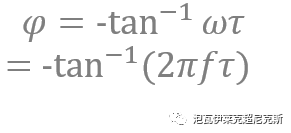
    百度一下，白嫖個函數圖像：

    為了避免用大一高等數學的泰勒展開和各階近似把人繞暈，直接由圖可知：

x→0（無窮小），有y=-x成立；x=1時，y=-x*pi/4。

    如果你愿意，可以把這段區域用y=-x和y=-x*pi/4包起來。

    因此，知道了相角，由高中數學三角函數知識，顯然可以得到對應的時間：

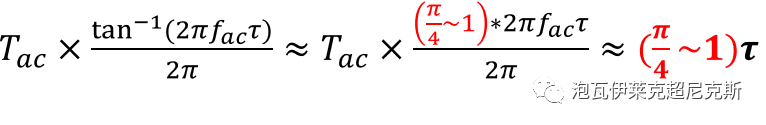
    結論：近似的，通過時間常數為τ的一階系統，若輸入的交流信號頻率處于相對中低頻（低于轉折頻率fc），輸出產生的延遲約在0.785τ~τ之間。

總結下

    這就是大家的直覺印象，交流信號通過時間常數τ的濾波器，會產生大約τ的時域延遲的由來。

    但要注意，該結論的近似條件，只到轉折頻率fc，也就是低頻才可等效。

    某種程度上，這也直接從時域等效的角度，解釋了耳熟能詳的：在相對低頻段，τ的純延遲環節可以和時間常數τ的一階慣性環節，相互近似等效。

    如果從頻域的角度，畫出延遲環節（含e的超越函數）的波特圖曲線，可以發現在低頻段，其相角和一階系統差異很小。

    究其數學根本，就是高數的泰勒展開近似。感興趣的同學可以自行查閱陳伯時老師的“電力拖動自動控制系統”課本，附錄中針對該近似的推導。