LabVIEW圖像增強算法（基礎篇—5）

在采集或傳遞圖像的過程中常會受到各種噪聲的影響，這會導致其中包含的重要信息很難被讀取和識別。例如，不均勻的光照會使圖像灰度過于集中；攝像頭的數模轉換電路所產生的噪聲會使圖像質量降低；圖像顯示設備的局限性會造成圖像顯示顏色減少等。

因此，在對圖像進行分析處理之前，必須對圖像進行增強，使其更適合人或機器進一步分析處理。

圖像增強是圖像處理的一個重要分支。它針對給定圖像的應用場合，通過各種算法增強圖像中的有用信息，有目的地強調圖像的整體或局部特性，抑制不感興趣的區域，擴大圖像中不同特征之間的差別，改善圖像質量，加強圖像判讀和識別效果，使圖像更能滿足分析或機器決策的需要。

圖像增強一般并不能增加原圖像信息，但是能針對一些成像條件，突出微弱信號，使信息更容易分辨。圖像增強算法根據處理過程所在的空間不同，可分為基于空間域的算法和基于頻率域（變換域）的算法兩大類，如下圖所示：

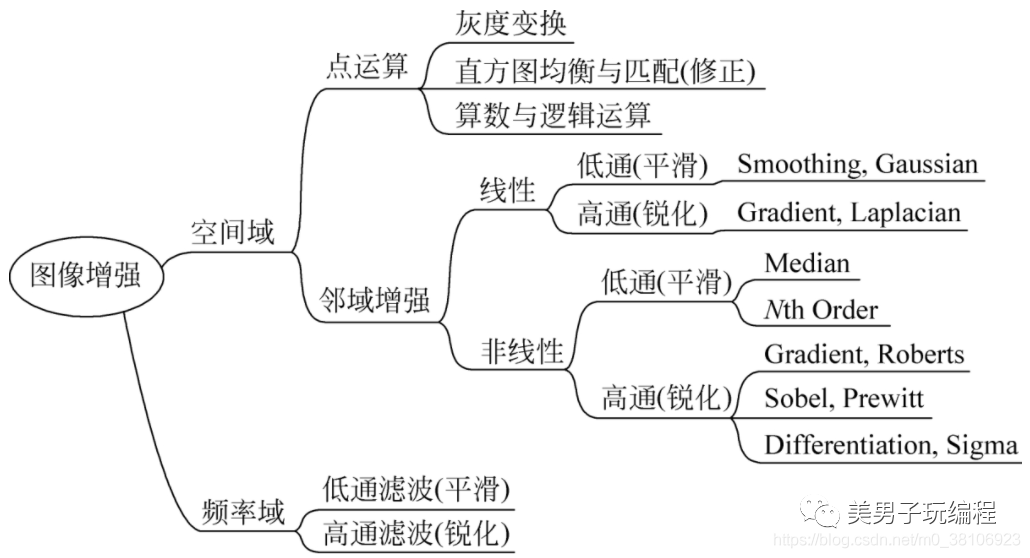
在空域中，圖像增強主要通過對不同位置的像素灰度及其變化方向進行操作來實現，而在頻域中圖像增強則主要通過對空間頻率（spatial frequency）進行操作來實現。

除了為圖像理解和機器識別、決策作準備外，圖像增強自身的應用領域也十分廣闊。例如：在軍事應用中，可增強紅外圖像中感興趣的敵軍目標；在醫學應用中，可增強X射線所拍攝的患者腦部、胸部圖像來確定病癥的準確位置；在空間應用中，對用太空照相機傳回的圖像進行增強處理以改善圖像的質量；在農業應用中，增強遙感圖像以了解農作物的分布；在交通應用中，對大霧天氣圖像進行增強以加強車牌、路標等重要信息進行識別等。

1

空間域圖像增強算法

空間域圖像增強算法直接對圖像進行點運算或鄰域處理。

點運算直接對像素灰度進行點對點映射，常見的點運算包括：灰度變換、直方圖匹配（修正）和直方圖均衡，以及某些圖像的算數或邏輯運算等。圖像的鄰域增強則以某一像素為中心，綜合該像素及其周圍某一范圍內（鄰域）像素的灰度值進行計算，并將計算結果作為中心像素新的灰度值。

根據輸出像素是否是輸入像素及其鄰域內像素的線性組合，可將圖像鄰域增強方法分為線性和非線性兩大類。每一類方法又可分為低通濾波和高通濾波方法。低通濾波算法可以濾除圖像中的高頻噪聲，使其變得更平滑；高通濾波則可以增強圖像中目標的輪廓或邊緣等高頻細節，使其更銳化。

1.1、線性卷積

1.1.1、一維卷積

圖像在空間域的增強常通過線性卷積運算來實現，它通過在圖像中滑動一個模板，不斷根據鄰域像素的值計算各個像素的新值來完成計算過程。

根據信號處理理論，線性時不變系統可通過其傳遞函數來描述。如果忽略線性系統的內部細節，則線性系統在時域可抽象為輸入信號f(t)與其傳遞函數沖擊響應h(t)的卷積(Convolution)，在頻域則可抽象為輸入信號F(s)與其傳遞函數沖擊響應h(s)的乘積。下圖顯示了基于傳遞函數的線性系統模型：

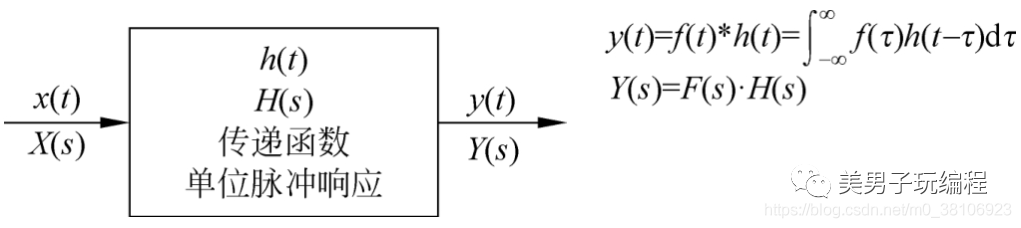
卷積運算為積分運算，它反映了函數h(T)被反轉為h (-T)后，沿r軸在另一個函數f(T)上移動時，與其所重疊部分乘積的積分。下圖顯示了兩個函數進行卷積計算時的反轉、平移及相乘和積分過程。

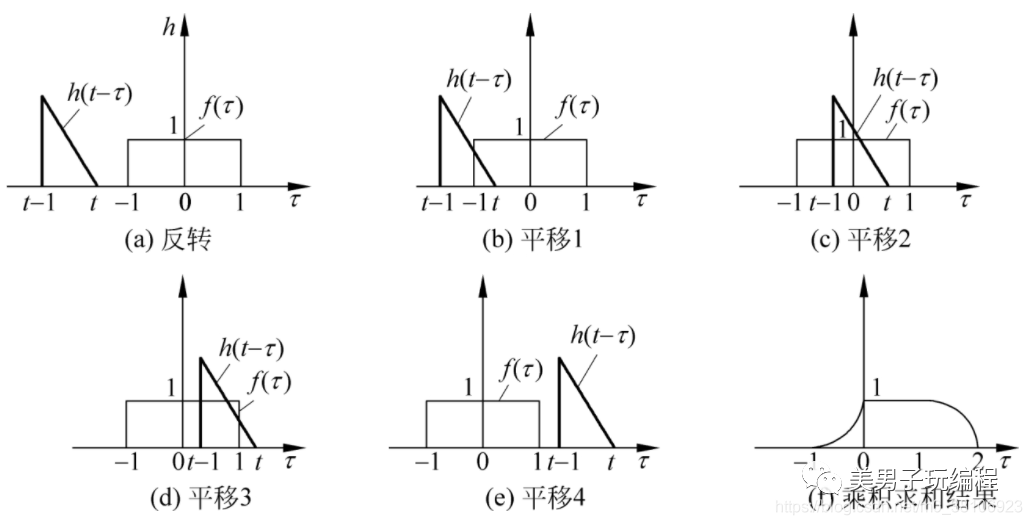
對于離散信號來說，假定有兩個長度分別為m和n的序列f(i)和h(j)，則它們的積分將輸入長度為(m+n-1)的序列，可表示為：

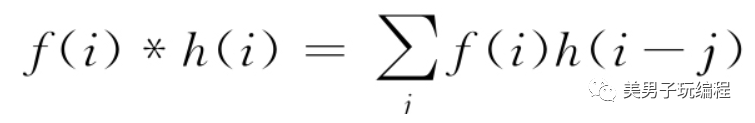
離散信號的卷積過程與連續信號類似，不同之處在于其中一個序列被反轉、平移后，與另一序列重疊的對應點相乘后是進行求和運算。下圖顯示了兩個離散序列的卷積計算過程：

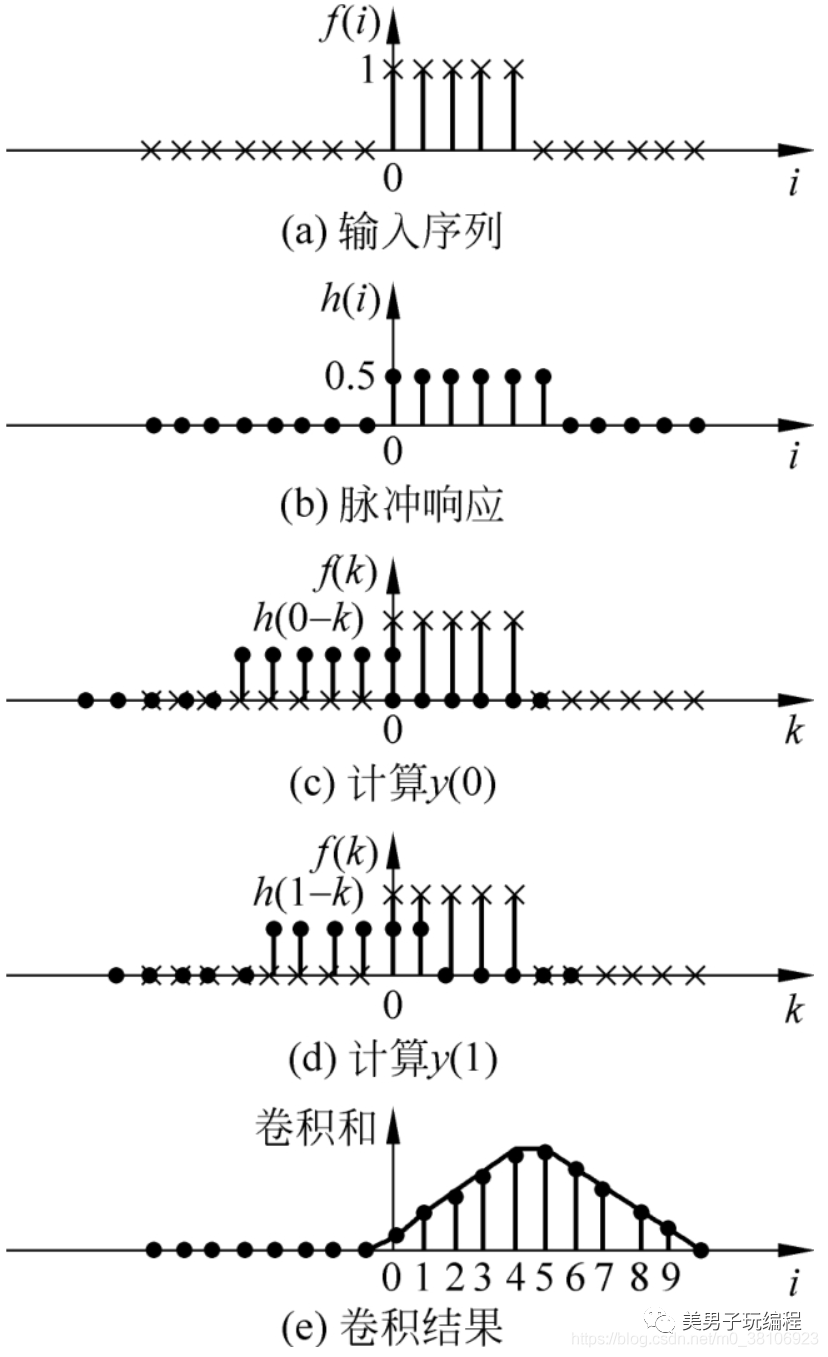
如果換個角度，將其中一個序列反轉后的值看作是它與另一序列重疊時對應點的權重，則卷積可以被看作是“加權求和”操作。

若再進一步，反轉后的序列的值均為歸一化后的值，則卷積可以被看作是對一組序列進行“加權平均"操作。若線性時不變系統為二維系統，則可表示為以下連續和離散形式：

連續形式為：

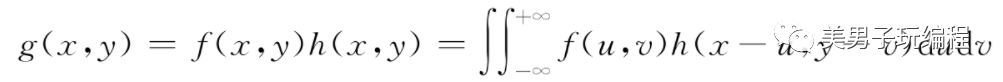
離散形式為：

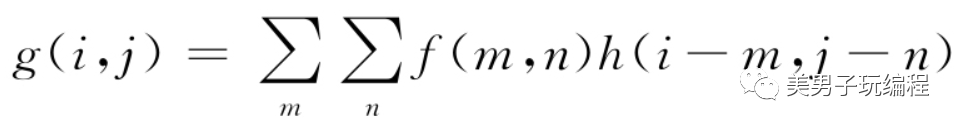
此外，如果二維線性系統可分離，即h (x, y) =h1(x)h2 (y)，則線性系統可分解為兩個一維卷積：

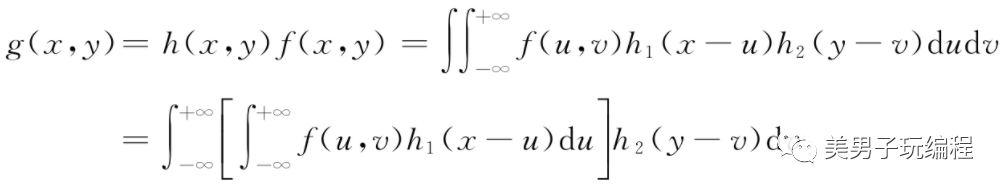
離散形式為：

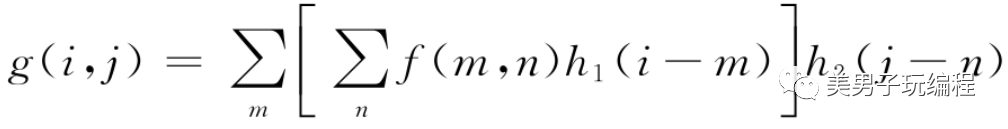
這意味著在進行二維卷積計算時，可以將其分解為連續的兩次一維卷積計算。在工程實踐中，這種分解往往會極大地降低程序算法的計算量，提高計算速度。

1.1.2、二維卷積

二維連續信號的卷積計算過程與一維卷積邏輯上類似。

計算時可以先將其中一個信號h(u，v)沿其原點旋轉180°，然后以原點為中心沿u軸和v軸平移該信號（u軸平移x，v軸平移y）再將兩個信號重疊部分相乘并積分，即得到原點處的輸出。若信號為二維離散信號，則可以先將其中一個離散點陣序列h(m，n)沿其中心點旋轉180°，然后以中心點沿另一離散點陣序列f(m,n)的橫向和縱向滑動，每到一個位置，就把兩個序列重疊的對應元素（中心點的鄰域）相乘并且求和，即可得到該點的卷積。

若將離散二維信號f (m，n)看作是待處理的數字圖像，并使h(m，n)點陣沿其中心對稱（即旋轉180°前后結果相同），就可以通過直接在數字圖像f(m，n）中滑動h(m，n)完成圖像的卷積運算。此時，被旋轉180°后的h(-m，-n)點陣或沿中心對稱的離散點陣h(m,n)被稱為模板或卷積核（converlution kernel）。

圖像卷積計算屬于一種鄰域處理方法。理論上來說，卷積核可以為任意尺寸，但是為了處理方便，它實際上常被設計為3×3、5×5或7×7等方形陣列。卷積核的類型決定了卷積運算對圖像中的像素如何進行變換，卷積核中的元素值（權重）定義了它所覆蓋的像素對中心像素的影響。在計算時，將卷積核由圖像的左上角到右下角逐點平滑移動，每次滑動至一個新像素，都將卷積核中的每一因子作為權重值（絕對值越大，對中心點的影響越大），與它所覆蓋的圖像范圍內的像素做加權求和，得到的結果作為它所覆蓋的圖像部分中心點的像素值。

下圖顯示了使用一個大小為3×3的卷積核對圖像進行卷積運算時的過程。卷積核沿著圖像左上角逐行、逐列滑動至右下角最后一個像素點。對于每次移動，卷積核中的9個元素P(x，y)都會和它覆蓋的圖像中對應的像素K(x，y)相乘并求和，得到的結果∑K (x, y)·P (x，y)將作為卷積核中心點在圖像中所覆蓋的像素P(x，y)的新值。當卷積核沿著所有像素滑動，并均完成前述計算后，圖像的卷積計算即完成。

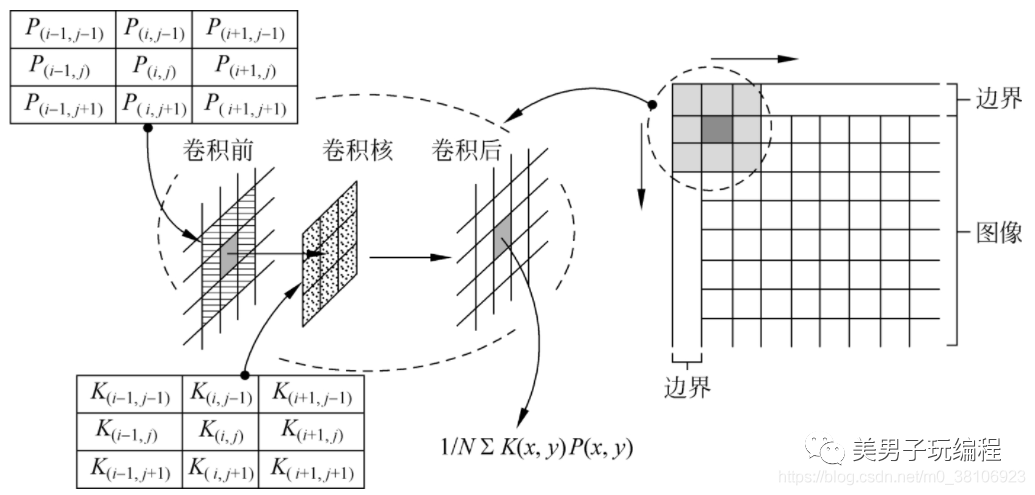
在機器視覺和圖像處理系統開發過程中，卷積運算常用于對圖像在空間域進行增強。具體是濾除圖像中的噪聲還是增強目標的輪廓或邊緣等高頻細節，由所選擇的卷積核決定。

1.2、領域增強

圖像的鄰域增強，就是在空間域對其進行高通或低通濾波，以消除其中的噪聲，銳化圖像的輪廓，沿某一方向銳化目標的邊緣等。

圖像的空間域濾波直接根據像素及其周圍鄰域內的像素值，通過某種計算或變換得到新的像素值來實現濾波功能。如果輸出像素是輸入像素及其鄰域像素的線性組合，則稱為線性濾波，否則稱為非線性濾波（中值濾波、邊緣保持濾波等）。例如，基于卷積的圖像鄰域加權求和濾波就是一種空間域的線性濾波方法，而中值濾波等非加權計算形式的濾波則為非線性濾波。

一般來說，線性平滑濾波對去除各種噪聲（如高斯噪聲）較為有效。但是當信號頻譜與噪聲頻譜混疊，或者當信號中含有非疊加性噪聲時（如由系統非線性引起的噪聲或非高斯噪聲等），線性濾波在濾除噪聲時，總會以某種方式模糊圖像中的邊緣和細節，進而降低圖像中線性特征的可識別性。非線性濾波器常基于某種非線性映射關系，把某一特定的噪聲近似地映射為零而保留信號的重要特征，因而其在一定程度上能克服線性濾波器的不足之處。

NI Vision為圖像的鄰域增強提供了眾多濾波函數，它們位于LabVIEW的Vision and Motion→Image Processing→Filters圖像空間域濾波函數選板中。使用這些函數可以對圖像進行線性或非線性高通、低通濾波，實現銳化圖像中目標邊緣、輪廓和細節或對其進行平滑降噪的功能。位置如下所示：

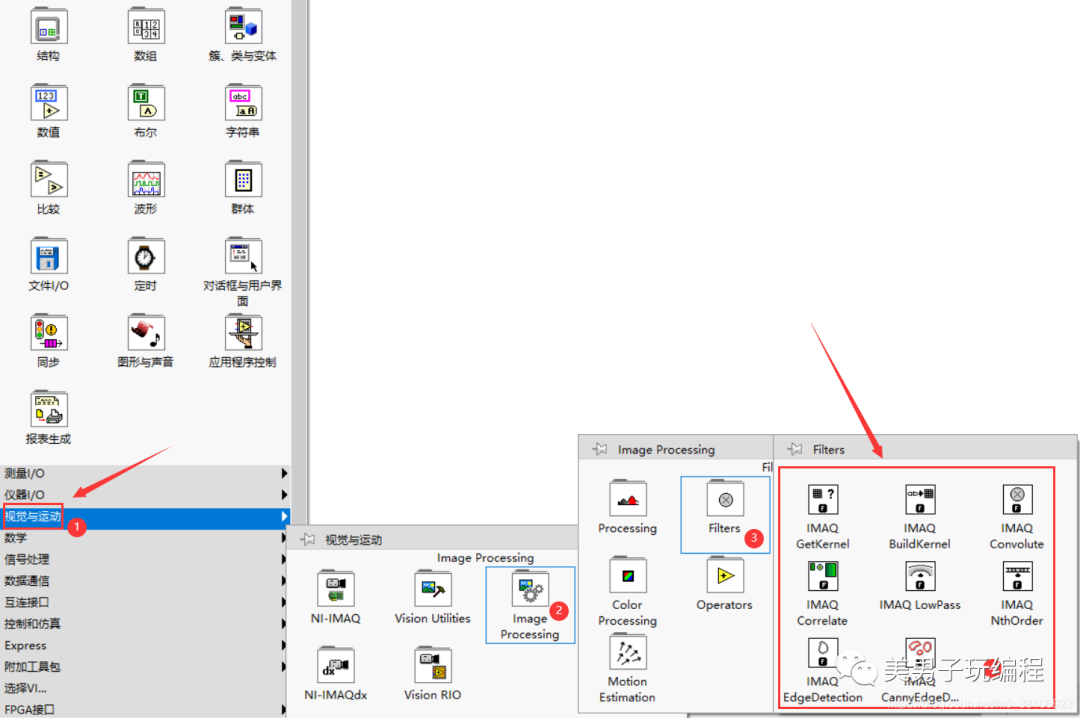
函數說明及使用可參見幫助手冊： 

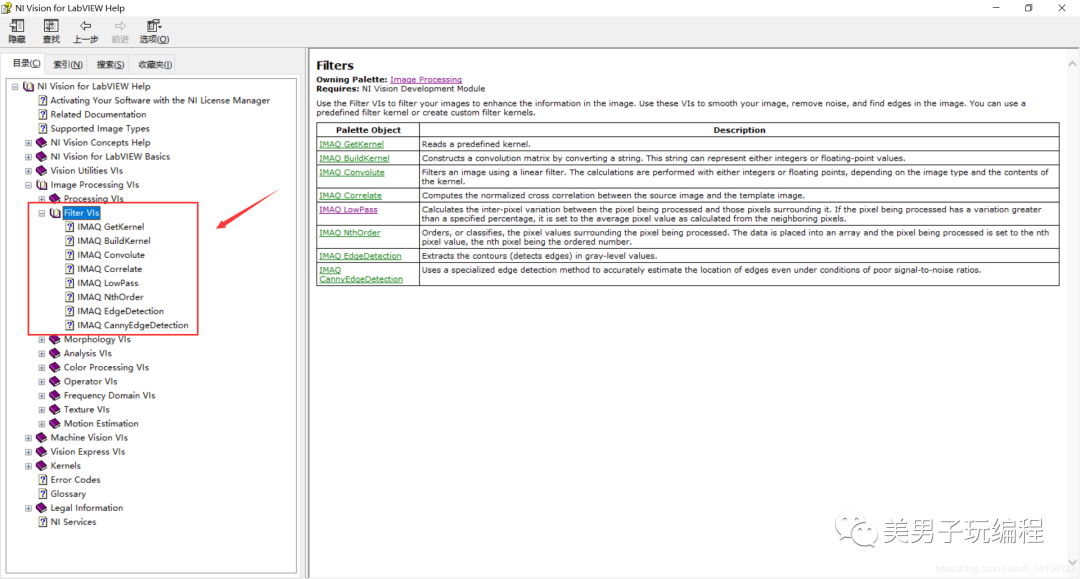
1.2.1、線性濾波

機器視覺系統開發過程中，常用的基于卷積計算的線性濾波方法有線性梯度算子（Linear Gradient）、拉普拉斯算子（Laplacian）、平滑濾波（Smoothing）和高斯算子（Gaussian）4種。其中，前兩種方法用于銳化圖像中灰度變化較快的高頻邊緣或紋理細節；后兩種方法則用于濾除高頻噪聲和細節，使圖像更平滑。下表對常用的線性濾波方法進行了匯總：

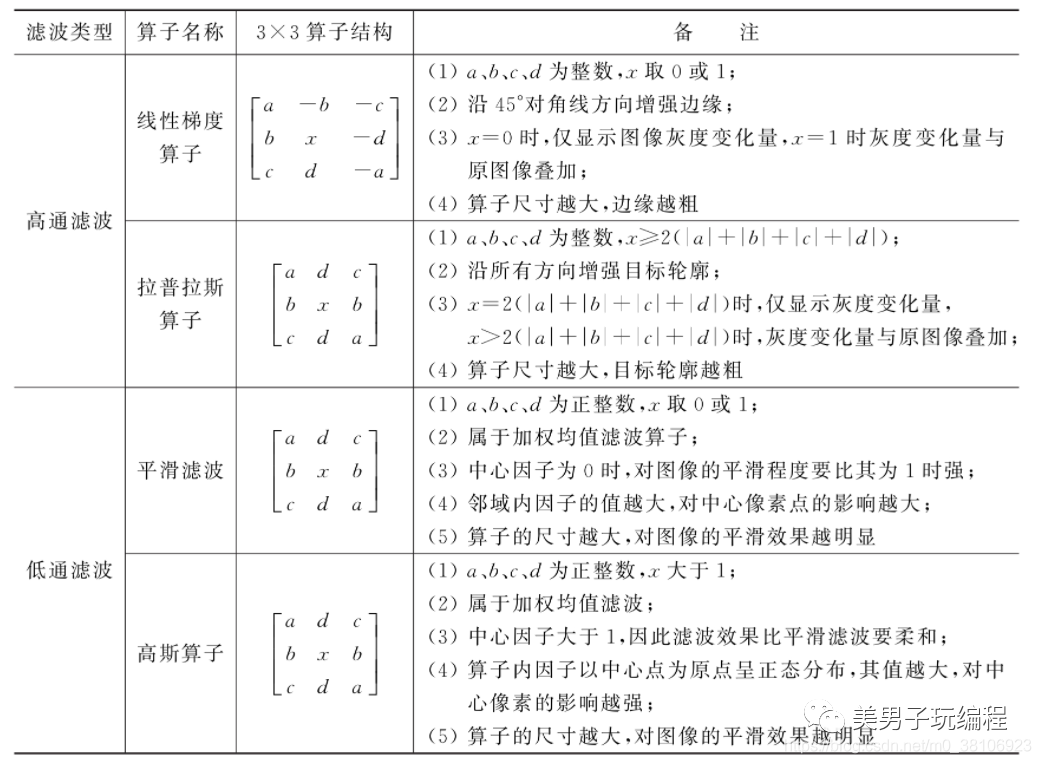
鄰域增強中的線性濾波多基于卷積運算，卷積核的尺寸限定了處理時的鄰域大小，卷積核中的元素值設定了各鄰域像素對中心像素影響的權重值，其絕對值越大，對中心像素的影響越大。如果卷積核中的因子有正有負，則濾波過程相當于鄰域像素求權重差，其效果相當高通濾波；而如果卷積核中只有正因子，那么濾波過程相當相當于鄰域像素求權重和，其效果相當低通濾波。線性梯度、Laplacian算子屬于前一類，而高斯和平滑濾波屬于后者。

Nl Vision使用IMAQ Convolute和IMAQ GetKernel或IMAQ BuildKernel配合，在空間域對圖像進行線性濾波。

IMAQ Convolute可使用由Kernel參數指定的卷積核對圖像進行卷積運算，而IMAQ GetKernel和IMAQ BuildKernel則用于獲取Nl Vision預定義的卷積核，或由字符串構建卷積核，以傳遞給IMAQ Convolute的Kernel參數，如下圖所示：

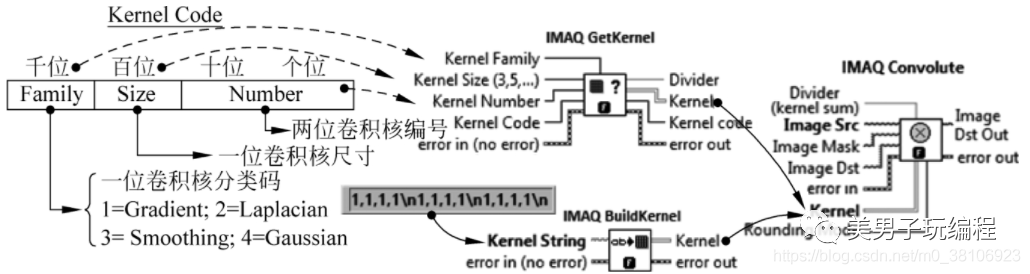
IMAQ BuildKernel搜索由逗號或分號分隔的字符串（各行由換行符分隔），將其中的數字轉換為卷積核；IMAQ GetKernel通過卷積核的編碼（Kernel Code）來索引NIVision預定義的卷積核。卷積核的編碼由4位數字構成，其中千位代表卷積核的分類碼(Kernel family)，百位代表卷積核的尺寸（Kernel Size），個位和十位共同代表卷積核的編號（Kernel Number）。例如，大小為3×3的梯度算子中，第14個算子編碼為1314。

Nl Vision共預定義了梯度、拉普拉斯、平滑和高斯4大類卷積核，不同卷積核的大小、作用各不相同，且都能通過卷積核的類別、尺寸及編號進行索引。

1.2.2、非線性濾波

非線性濾波方法也可分為進行邊緣檢測的高通濾波和去除圖像中雜散點的低通濾波兩大類。

常用的非線性邊緣檢測（高通）方法有非線性梯度（Nonlinear Gradient）、Roberts、差值（Differentiation) 、Sobel、Prewitt、Sigma和Canny 7種。非線性低通濾波方法則有中值（Median）濾波、N階濾波器、低通(Lowpass）濾波3種。下表對常用的非線性濾波方法進行了匯總：

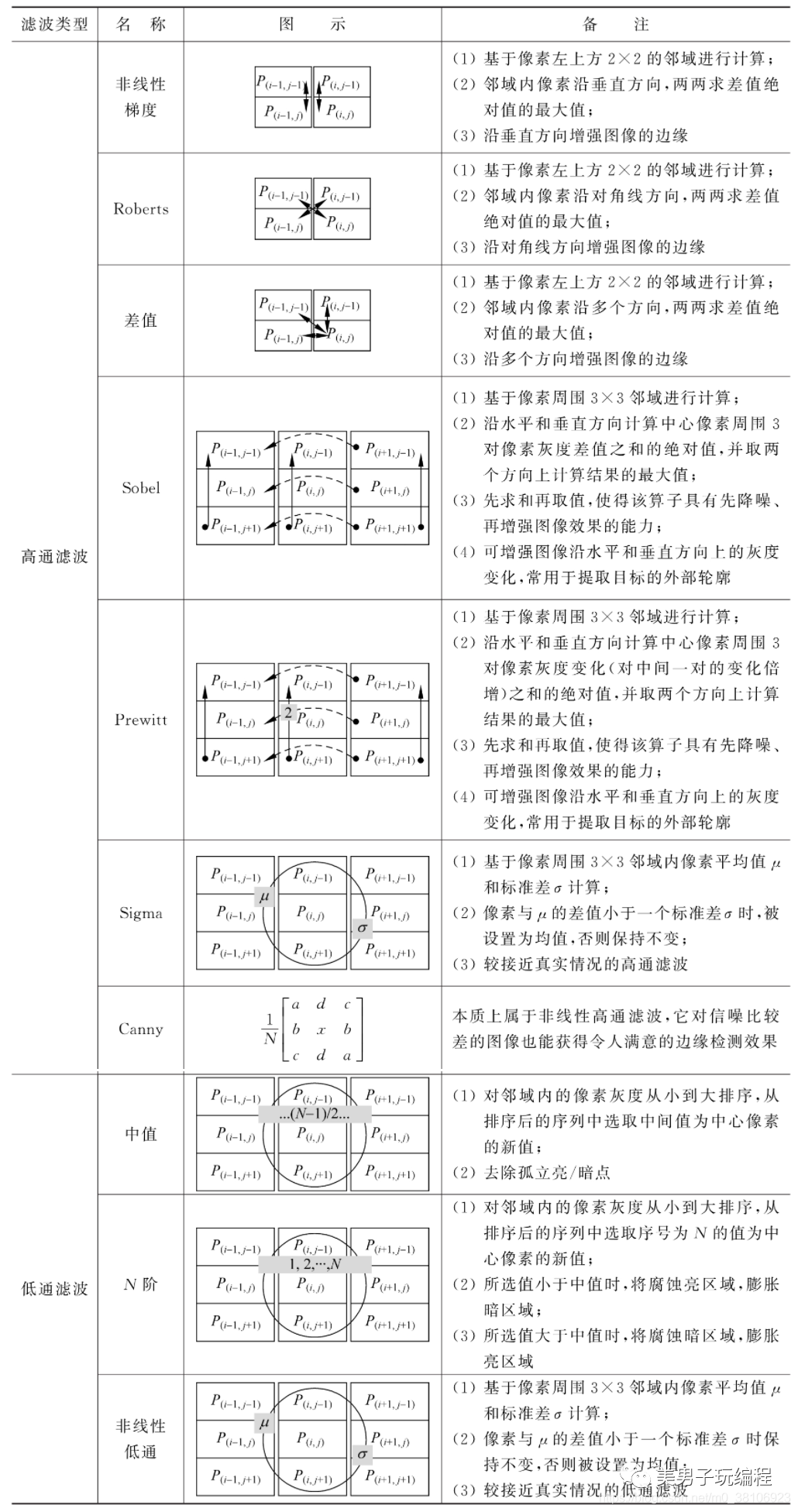
與線性濾波方法類似，空間域的非線性濾波方法也常使用濾波算子，基于像素的鄰域進行計算，但是其計算函數往往并非線性函數。若用P (x，y)格式表坐標為(x，y)的像素值，則可通過像素灰度的非線性函數來表示各種非線性濾波算法。

非線性梯度、Roberts和差值濾波過程均基于像素左上方2×2的鄰域進行。非線性梯度濾波對該鄰域內的像素兩兩沿垂直方向求其差值的絕對值，并取其中較大者作為新像素值。Roberts濾波過程與非線性梯度濾波計算過程類似，但它是沿對角線方向，對像素左上方向2×2鄰域內的像素兩兩求差值的絕對值，并取其中較大者作為新元素值。差值濾波過程則對像素左上方向2×2鄰域內的像素，沿各個方向兩兩求差值的絕對值，并取其中較大者作為新元素值。

通過使用IMAQ Convolute對圖像進行平滑濾波、IMAQ EdgeDetection對圖像進行非線性高通濾波（包括非線性梯度、Roberts、差值、Sobel、Prewitt濾波和下面將要講到的Sigma濾波）、IMAQ LowPass和IMAQ NthOrder實現圖像的非線性低通濾波、IMAQ CannyEdgeDetection實現Canny算法的實例程序了解線性濾波、非線性濾波和Canny算法的使用方法，由于這是一個程序中集成了多個圖像處理功能，分別講講各個功能設計思路。

線性濾波功能模塊設計思路如下所示：

• 程序一開始先為圖像處理分配內存，并將圖像fig.tif讀入內存緩沖區，然后進入While循環；

• While循環首次執行時，將比較用戶所選擇的濾波方式Filter及各圖像增強VI的參數Kernel Size、Kernel#、Size & Tolerance及Size & Order是否與Parameter簇常量中的默認值不同，若有變化，程序即進入包含各種濾波Vl的分支；

• 當從Filter控件中選擇Smooth濾波方式時，分支結構中的代碼將調用IMAQ GetKernel，根據輸入參數獲取NIVision預定義的卷積核，并傳遞給IMAQ Convolute對圖像進行卷積運算；

• 當循環繼續執行時，程序將比較用戶的輸入與上次循環執行時是否有變化，若任何輸入發生變化,程序都會再次進入包含濾波代碼的分支；

• 當用戶單擊STOP按鈕時，程序將退出循環釋放緩沖區，結束程序執行；

• 實例中，用戶選擇了對圖像進行平滑濾波，所選用的卷積核大小為5×5，編號為#0。

非線性高通濾波功能模塊設計思路如下所示：

只需通過它的Method參數選擇所需的濾波方式即可。程序結構與線性濾波功能代碼結構相同，只是從樹形列表控件中選擇了Differentiation濾波方式，從而代碼也相應執行非線性差值高通濾波分支。由程序的運行結果可以看出，濾波后的圖像邊緣沿多個方向被增強。

非線性低通濾波功能模塊設計思路如下所示：

• 程序中顯示了基于3×3鄰域對圖像進行N階非線性低通濾波的實例；

• 由于N取4，恰好為鄰域內像素排序后中間值的索引，因此相當于對圖像進行中值濾波；

• 由程序的運行效果可以看出，原圖像中的椒鹽噪聲幾乎均被濾除；

• 還使用IMAQ LowPass對圖像濾波，以及使用IMAQ NthOrder取N=1和N=7時對圖像濾波的結果。

  可以看出，當N階濾波器的階值小于4時，暗區域被膨脹，亮區域被腐蝕，而階值大于4時則恰好相反。

Canny算法功能模塊設計思路如下所示：

• Canny算法采用高、低雙閾值法減少假邊緣點的數量；

• 若某一像素位置的值超過高閾值，該像素被保留為邊緣點；

• 若小于低閾值，則被去除;若在兩個閾值之間，則僅當像素與一個高于高閾值的像素連接時才被保留；

• Canny算法推薦高、低閾值的比例在2:1到3:1之間。

  可以較為準確、有效地確定圖像的邊緣。

程序實現如下所示：

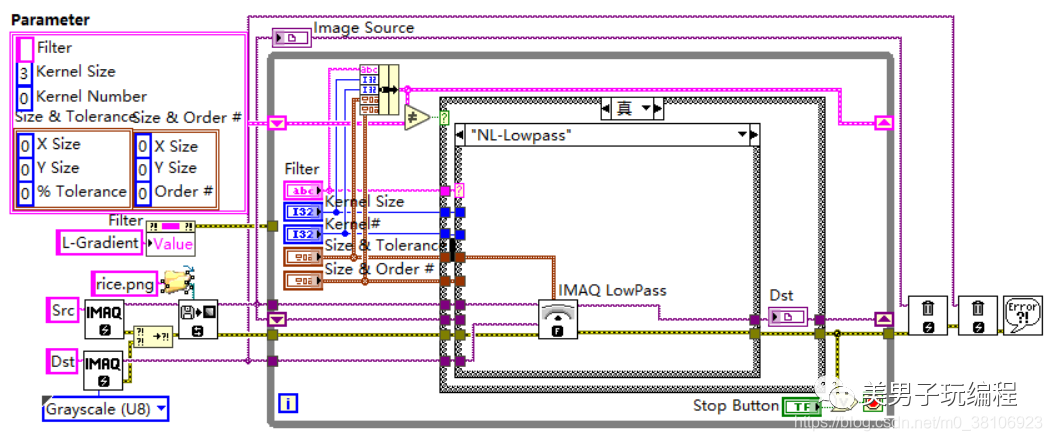
程序效果如下所示：

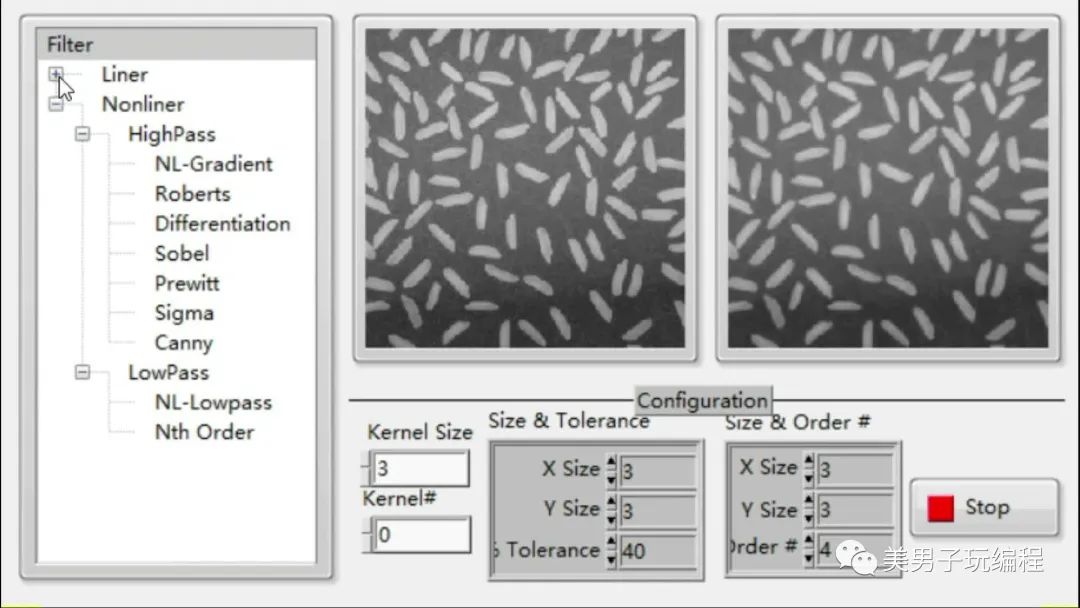
2

頻率域圖像增強算法

2.1、傅里葉變換算法

與空域濾波的工作方式不同，頻率濾波器并不直接對圖像像素數據進行操作，而是先通過快速傅里葉變換將圖像轉換至頻率域，經濾波處理后再由傅里葉逆變換（InverseFFT）轉換回空域，以達到圖像增強的目的，如下圖所示：

相對于空域濾波來說，頻域濾波有以下兩點主要優勢：
1、空域在處理某問題時比較困難，甚至幾乎難以處理；
2、將圖像處理問題從空域轉換到頻率域上處理時，可以使用一系列成熟的數字信號處理方法和工具集。

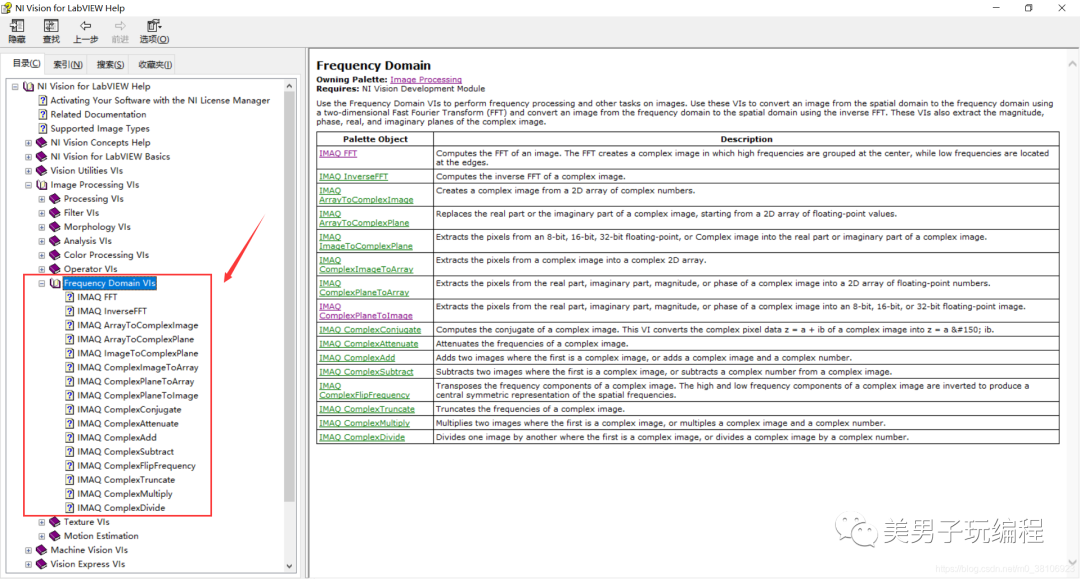
Nl Vision為傅里葉變換以及圖像頻域計算提供了現成的函數，它們位于LabVIEW的Vision and Motion→lmage Processing→Frequency Domain函數選板中，如下圖所示：

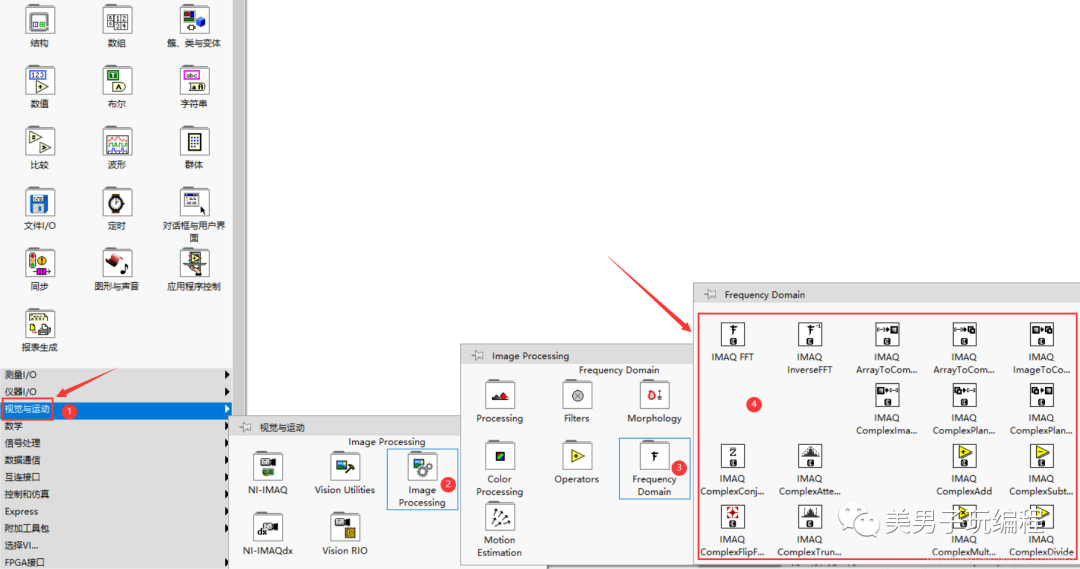
函數的說明和使用可參見幫助文檔：

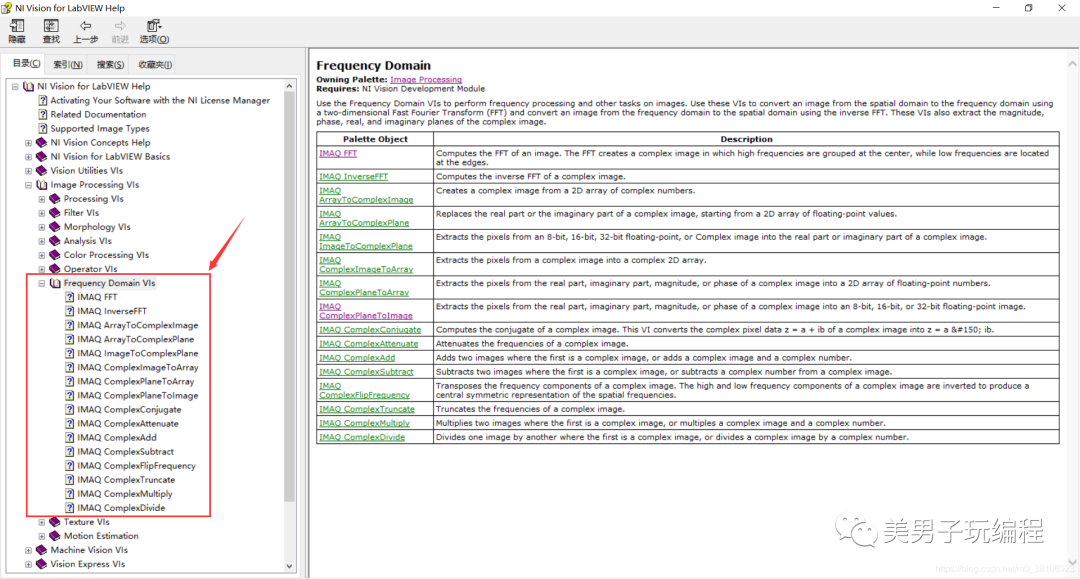
通過對一幅圖像進行FFT的實例，了解傅里葉變換的使用方法，程序設計思路如下所示：

• 程序一開始先將圖像讀入內存，并使用IMAQ Cast lmage將其轉換為復圖像；

• 函數IMAQ FFT對復圖像進行FFT后，其輸出被連接到圖像顯示控件進行顯示；

• IMAQ ComplexPlaneTolmage用于提取復圖像的實部、虛部、幅度或相位，并以8位、16位或32位浮點數圖像格式表示；

• 在本例中，在它從FFT的變換結果中提取出幅度數據并顯示在控件MagF中后，程序將釋放所有緩沖區并退出。

程序設計如下所示：

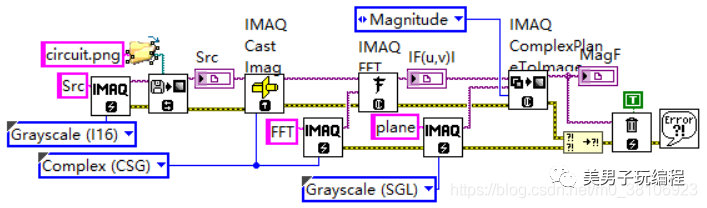
效果如下所示：

對比程序運行結果可以發現，使用圖像顯示控件直接顯示復數圖像與提取出幅度譜后再顯示的效果完全不同。這是因為Nl Vision在內存中使用標準方式組織FFT的計算結果（復數）。這意味著從FFT計算得到的幅度數據中，高頻部分將分布在圖像的四角，低頻區域在圖像的中心。但是，當使用圖像顯示控件直接顯示復數圖時，Nl Vision會自動計算圖像的幅度譜，并反轉高頻和低頻數據，以中心對稱模式顯示。即高頻部分居中，低頻部分分布在四角。不僅如此，為了增強幅度的顯示效果，NI Vision還會為計算得到的幅度數據乘以一個與圖像長M和寬N相關的系數m，其計算公式如下：

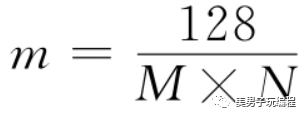
2.2、圖像頻域濾波

在圖像處理中，圖像的銳化與平滑處理可通過空間濾波或頻域濾波來完成。從數學角度看，空間濾波是將信號與濾波算子進行卷積等運算的結果，具有方法直觀、操作簡便等優點。但當要處理的圖像數據較大時，若沒有發現比較高效的算法，就會有計算量大、計算時間長以及實時性差等缺點。

在頻域對圖像進行分析、增強時，不僅無須求解較難的微分方程，而且利用頻譜圖可直觀地揭示系統性能，并可方便地選擇有效抑制噪聲的濾波器。此外，在頻率域上進行圖像處理時，還可以使用數字信號處理的一系列成熟方法和工具快速解決問題。

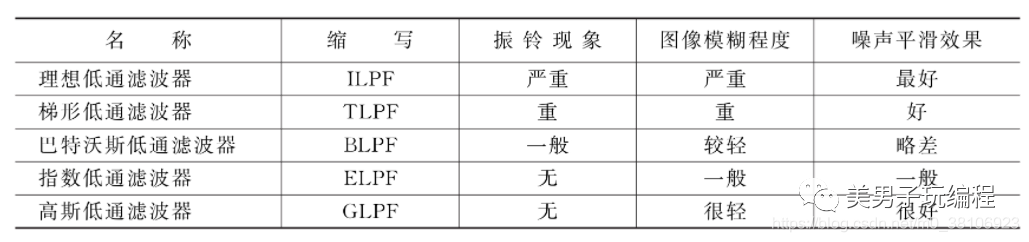
下表對常見的頻域低通濾波器的特點進行了匯總和比較，可以看出：

• 理想低通濾波器處理的圖像極為模糊，且含有很嚴重的振鈴現象，但其對噪聲的平滑效果好；

• 梯形低通濾波器的振鈴現象不像理想濾波器那樣嚴重；

• 巴特沃斯低通濾波器與指數低通濾波器相比，圖像模糊程度低，但對噪聲的平滑效果也差些；

• 高斯低通濾波器能在有效抑制噪聲的情況下盡可能減小圖像的模糊程度，因此它相對其他濾波器有較為廣泛的應用。

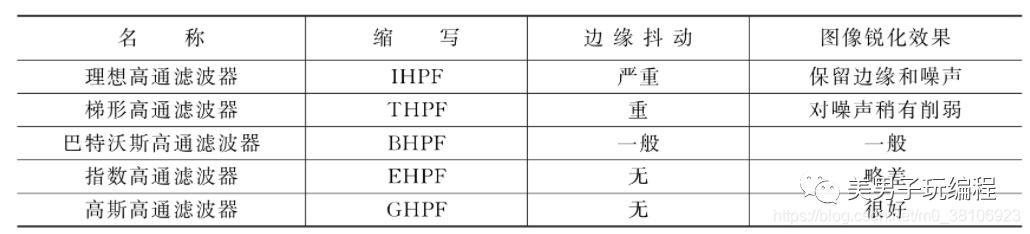
比較下表所列出的幾個高通濾波器可以發現：

• 理想高通濾波器處理的圖像邊緣抖動現象嚴重，且同時保留了邊緣和噪聲；

• 梯形高通濾波器會產生輕微抖動現象，但因計算簡單經常被使用；

• 巴特沃斯濾波器銳化效果較好，邊緣抖動不明顯，但計算復雜；

• 指數高通濾波器比巴特沃斯濾波器效果差些，無邊緣抖動現象；

• 高斯高通濾波器能在圖像邊緣抖動和銳化效果之間獲得較好的平衡。

帶通濾波器可以使某一下限和上限截止頻率范圍內的信號通過，但衰減低于下限截止頻率和高于上限截止頻率的信號。帶阻濾波器則可以衰減某一下限和上限截止頻率范圍內的信號，但允許低于下限截止頻率和高于上限截止頻率的信號通過。下圖顯示了理想帶通和帶阻濾波器的時頻響應：

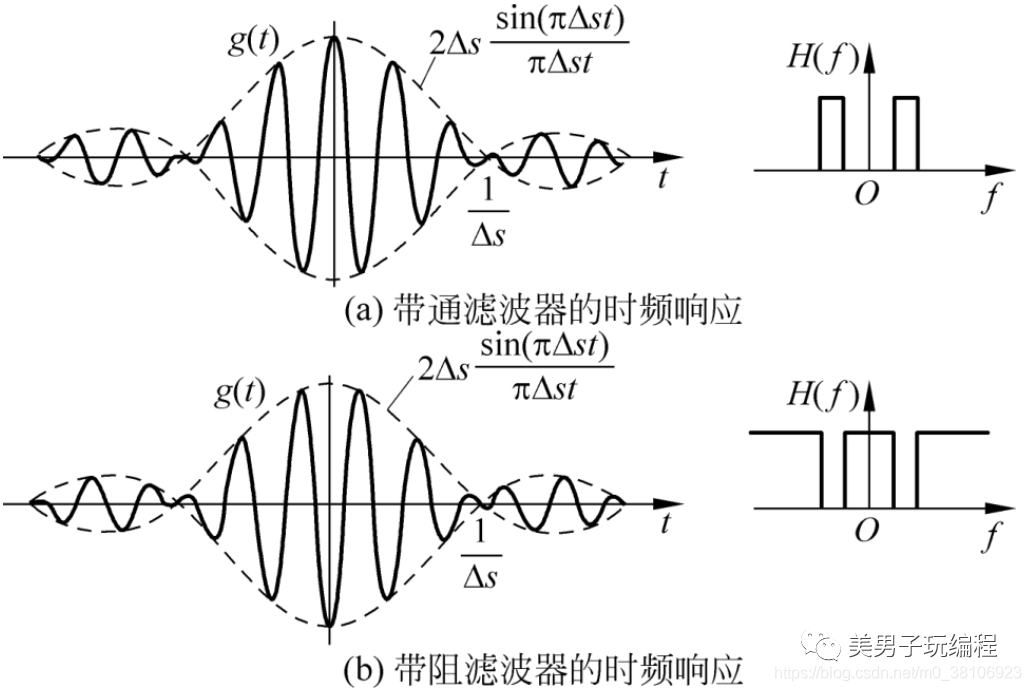
在實際中，帶阻濾波器常用于濾除圖像中的周期性噪聲。周期性噪聲在圖像的頻譜中常以對稱的形式出現，可使用帶阻濾波器濾除頻率在環形區域內的信號，以消除噪聲。可以看出，帶阻濾波器在去除周期噪聲時還會濾除噪聲以外的成分，使圖像中的有用信息減少。如下圖所示：

在LabVIEW中使用NI Vision進行圖像濾波的方法可以歸納為4類：

• IMAQ ComplexTruncate和IMAQ Mask可以使圖像中指定比例的頻率范圍通過或衰減，使用它們可以對圖像進行理想低通、理想高通、理想帶通和理想帶阻濾波；

• IMAQComplexAttenuate可對圖像進行三角形高通或低通濾波；

• IMAQ Mask除了可實現理想低通、理想高通、理想帶通和理想帶阻濾波器的功能外，還能實現理想陷波濾波器；

• 公式法則可以實現任何形式的頻域濾波器。

如下表所示：

NI Vision為頻域濾波操作提供了專門函數，它們位于LabVIEW的視覺與運動→lmage Processing→Frequency Domain函數選板中，如下圖所示：

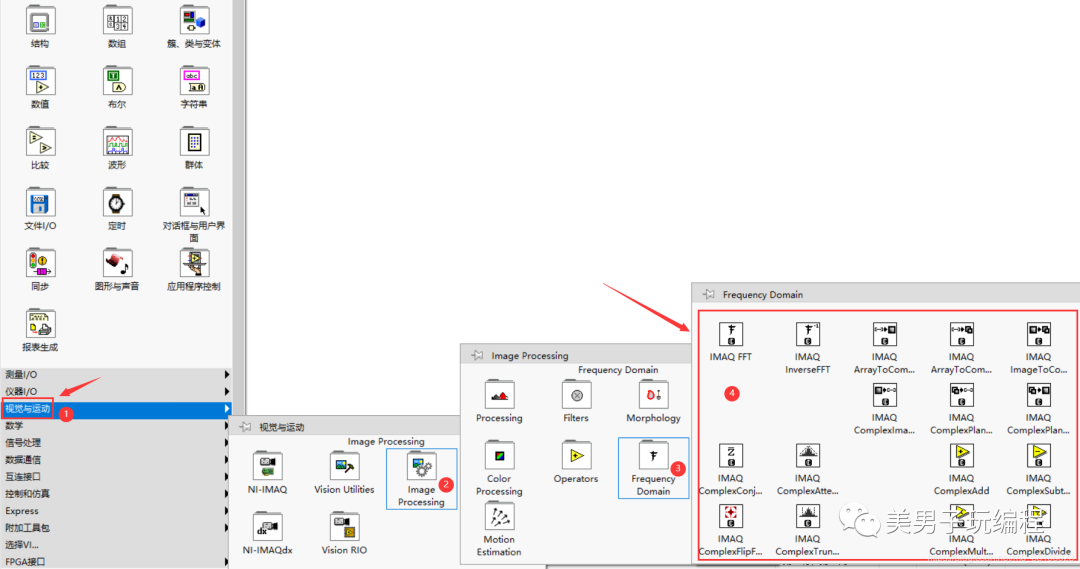
函數的說明和使用可參見幫助文檔：

通過一個圖像濾波示例，了解各類型濾波方法的使用方法，程序設計思路如下所示：

• 程序先將圖像讀入內存并對其進行傅里葉變換；

• 隨后使用IMAQ ComplexTruncate生成的理想低通濾波器對圖像進行濾波，其中參數Truncation Frequency%將低通濾波的截止頻率設置為圖像頻率范圍的5%處；

• 濾波完成后對圖像進行傅里葉反變換，獲得濾波后的圖像；

• 程序在為傅里葉反變換分配緩沖區時指定圖像類型為16位灰度圖，這樣NI Vision會自動對傅里葉反變換的結果進行轉換；

• 觀察程序運行結果，可以發現，使用理想低通濾波器對圖像進行濾波時會出現明顯的振鈴現象。

程序設計如下所示：

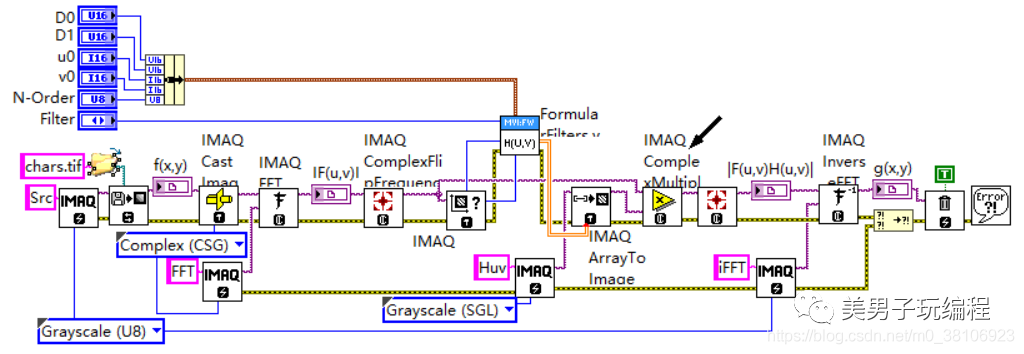
將IMAQ ComplexTruncate實現的理想低通和高通濾波器進行組合，可以實現理想帶通或帶阻濾波器。具體來說，當用其實現的低通和高通濾波器連續對某圖像進行濾波，且低通濾波器的截止頻率大于高通濾波器的截止頻率時，這種類似串聯的連續濾波結果等效于帶通濾波;當用其實現的低通和高通濾波器分別對原圖像進行濾波后將二者結果疊加，且低通濾波器的截止頻率小于高通濾波器的截止頻率時，這種類似并聯的濾波疊加效果等效于帶阻濾波。

程序效果如下所示：

圖像增強一般并不能增加原圖像信息，但是能突出微弱信號，使信息更容易分辨。圖像增強不僅可以在空域進行，還能在頻率域進行。在頻域處理圖像時，需要先通過傅里葉變換將圖像轉換至頻域，經濾波處理后再由傅里葉逆變換轉換回空域，以實現圖像增強。