開關電源環路學習筆記(6)-開關變換器傳遞函數Gvd(s)推導過程

終于到了最關鍵的環節，也是最難的環節，如何求出開關級的傳遞函數？

也就是下圖這一級。

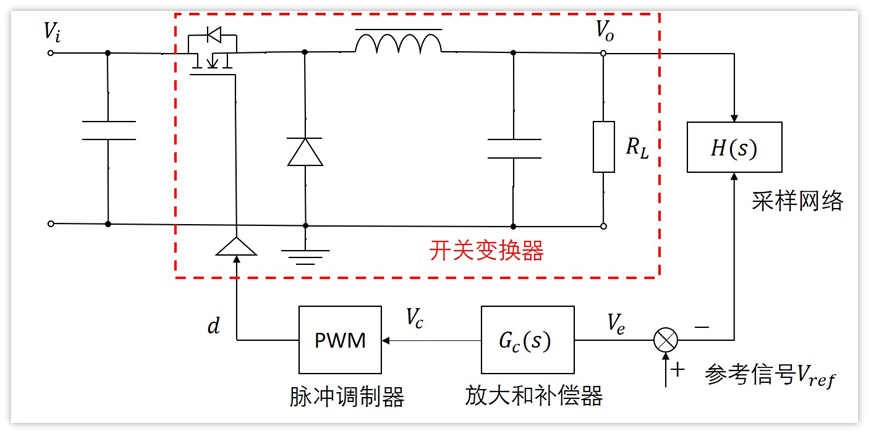
哎，不得不說，太難了。。。

不過沒辦法，先前夸下海口，跟兄弟們說我要把環路搞清楚，現在搞不動也得搞啊。

這一級之所以這么難，主要是有開關元器件，本身是非線性的。

當然了，前面第2小節我們已經闡明了，在滿足低頻，小信號等條件下，也可以看成是線性的，這里就不再說了。

那么如何求解傳遞函數呢？

求解方法

求的方法有很多種，常見的有下面這幾種：

1、小信號模型的建模思路——基本建模法

2、狀態空間平均法

3、開關元件平均模型法

4、開關網絡平均模型法

上面這幾種方法在《開關變換器的建模與控制+張衛平編著》這本書中都有非常專業詳細的講解。其實我此章也主要是看這本書進行的一個總結。

我個人覺得最好的應該是第4種——開關網絡平均模型法，或者說這是我最喜歡的方法吧，也是我深入去看的一種方法。

不過原書中的方法會畫出有變壓器的等效電路，我不喜歡引入變壓器，所以我下面介紹的過程是沒有引入變壓器的，直接推導出的公式。

Buck的CCM模式求解過程

求解過程主要有這么幾步：

1、二端口等效

2、端口參數關系，推導出兩個式子

3、代入電路，結合原理推導出傳遞函數

二端口等效

先來看二端口等效是怎么回事，下面是buck的拓撲。

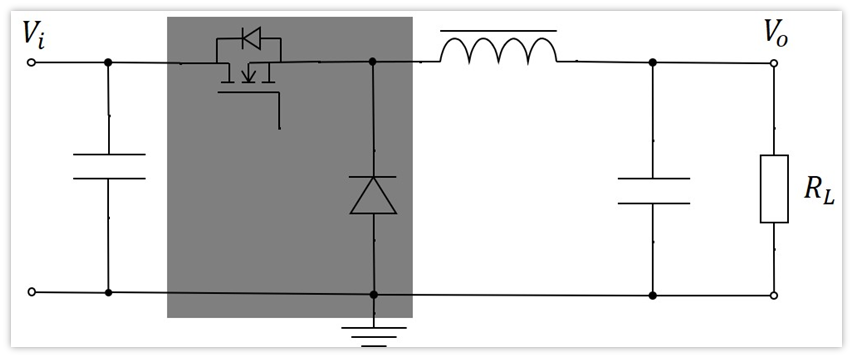
 最難搞的就是里面這個MOS管和二極管了，那咋整呢？

 干脆就把它看作一個整體，對外有四根線，同時底下兩根線接地，所以也就是說有兩個端口，是一個二端口網絡。

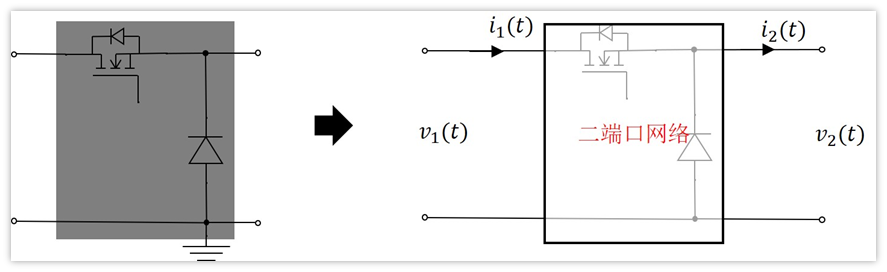
那么電路變成下面這樣的了

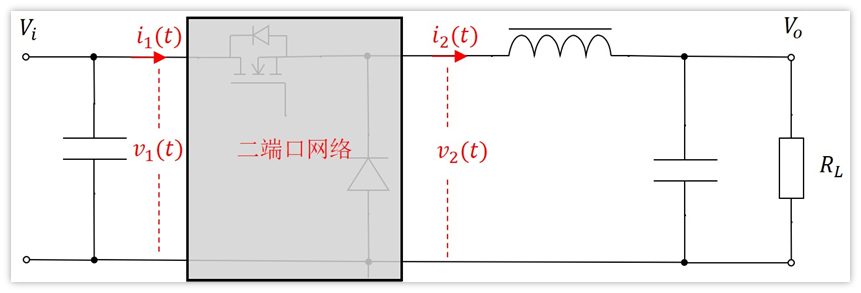
按照上圖一等效，好像也沒什么卵用，反而更加不熟悉了。先不著急

我們需要先對i1(t)，i2(t)，v1(t)，v2(t)取開關周期的平均值，注意，是開關周期平均值，而不是總時間平均值。因為如果是總時間的平均值，那就只是直流等效了。

這里多一嘴，說說開關周期平均值和總時間平均值有什么差別，因為我在這里想了比較久，并且看起來兩個值好像是一樣的。

確實，如果是穩態，沒有干擾信號，負載恒定，上述變量在每一個開關周期內的平均值都是一樣的，并且等于總時間的平均值。

但是如果有干擾信號，那么可能上一個周期的平均值跟下一個周期的平均值不一樣，也就是它是時間的函數。我們現在分析傳遞函數，就是分析干擾信號的影響，自然不能只看直流等效了，所以求的是開關周期的平均值。

那問題來了？求開關周期的平均值合理嗎？

其實這里就有用到前面所說的線性化條件——低頻信號假設，我們研究的信號大大低于開關頻率，因此求開關周期的平均值是合理的。

    取的周期平均值我們用新符號表示，分別為：I1(t)，I2(t)，V1(t)，V2(t)，它們都是時間的函數。那么電路就變成了下面這樣：

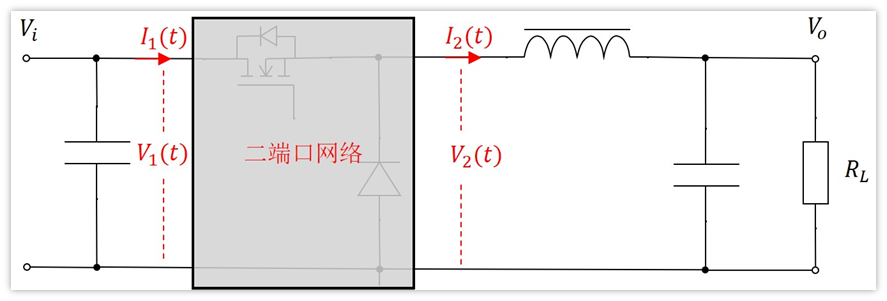
現在我們需要分析下我們引入二端口的4參數I1(t)，I2(t)，V1(t)，V2(t)，他們之間到底有啥恩怨情仇？

端口參數關系，推導出兩個式子

假如沒有任何干擾信號，那么I1(t)，I2(t)，V1(t)，V2(t)周期平均值和全時間的平均值是一樣的，每個周期都一樣，每個周期的平均值自然和全部時間內的平均值一樣，這應該沒毛病。

好，我們假設沒有干擾信號時，平均值分別是I1，I2，V1，V2，它們是個常量。此時開關信號的占空比也是恒定的，我們用D表示。

現在我們將干擾信號加進去，我們知道，系統只有滿足小信號條件的時候，才能將之近似看成線性系統。

既然干擾信號是小信號，那么這個干擾信號會引起I1(t)，I2(t)，V1(t)，V2(t)隨時間小范圍變化，它們分別以I1，I2，V1，V2為中心進行波動，同理，占空比也會圍繞D為中心進行波動。

各變量的波動量不就是交流小信號嗎？

我們分別用符號△I1(t)，△I2(t)，△V1(t)，△V2(t)，△D(t)來表示。

那么我們可以用下面的表達式進行表示：

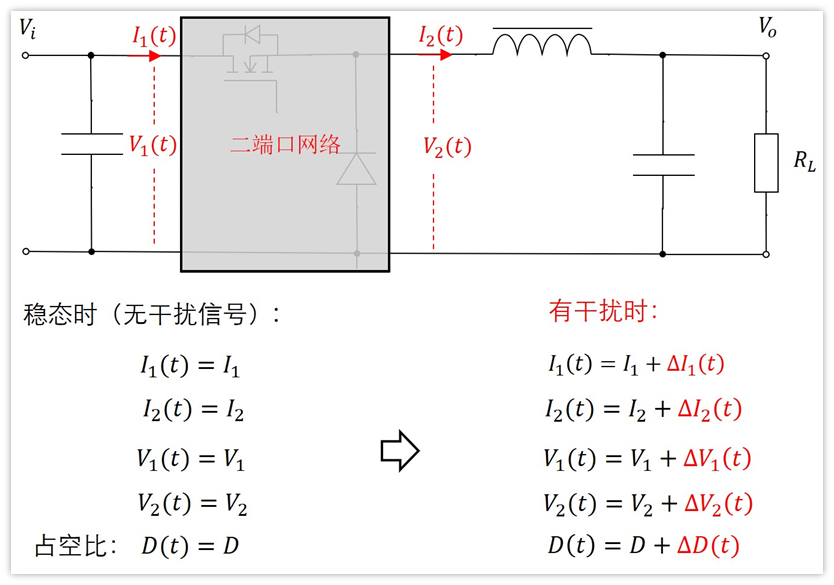
式子已經列出來了，現在我們需要求他們之間的關系。

先看看V2(t)的物理意義，前面說了，它是開關周期內的平均值。

顯然，V2(t)=V1(t)*D(t)，為什么呢？

因為在MOS不導通的時候，那么二極管導通，v2(t)為0，而在MOS導通的時候，v2(t)等于v1(t)。

所以，v2(t)在周期內的平均值V2(t)就等于導通時間的百分占比乘以V1(t)，即：

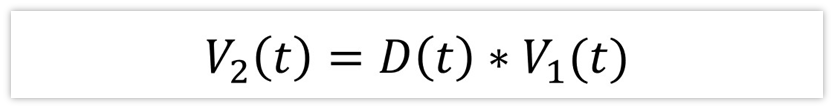
同樣的，I1(t)= I2(t)*D(t)，那又是為什么呢？

因為MOS在不導通的時候，i1(t)為0，而在MOS管導通的時候，i1(t)等于i2(t)，所以，i1(t)在周期內的平均值I1(t) 就等于導通時間的百分占比乘以I2(t)，即：

易知，上面兩個式子，無論是在穩態（沒有干擾），還是在有干擾的情況下，都是成立的。

小信號求解

我們把前面得到的幾個式子代換一下，就可以得到小信號的表達式。

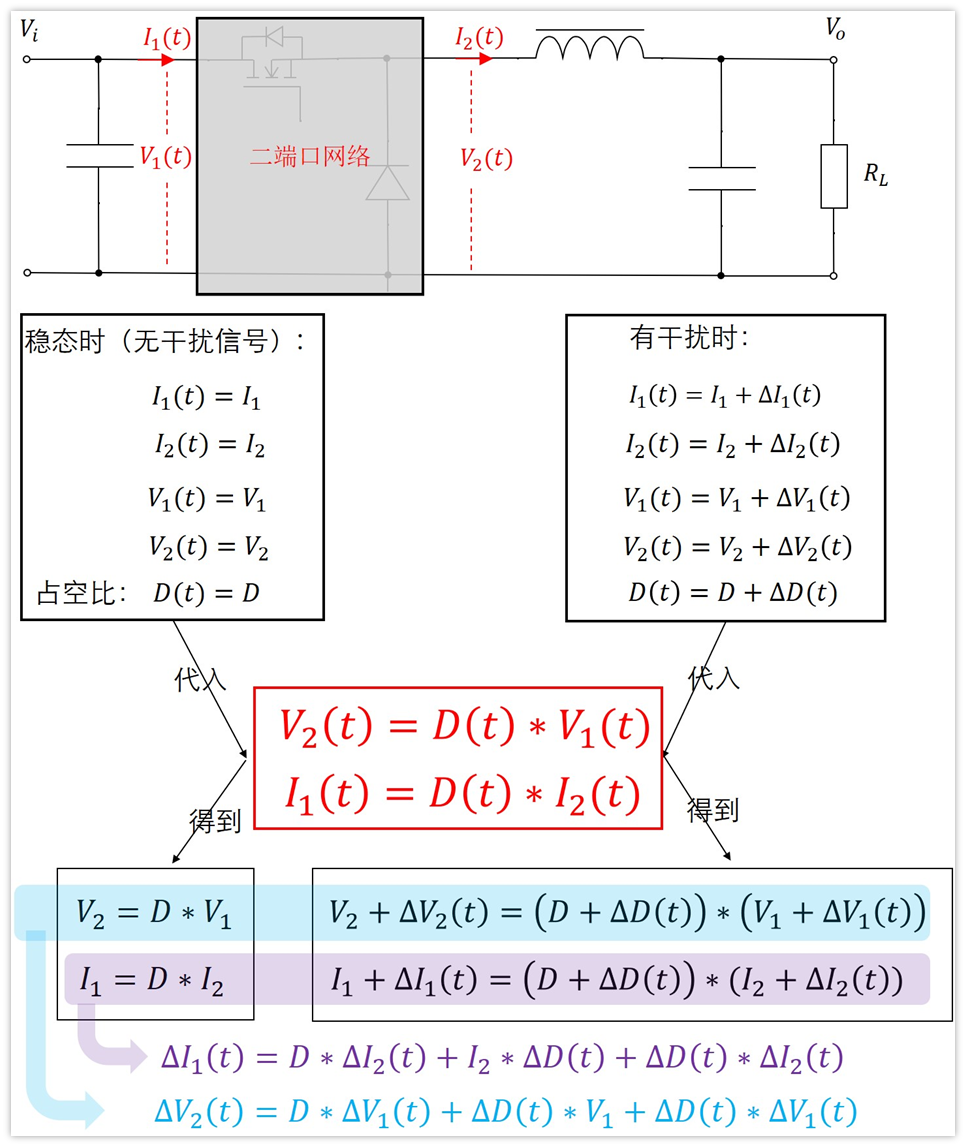
上面的式子可能看著有點復雜，其實簡單代換就出來了，最終我們得到了下面這兩個式子：

式子中忽略了高階微小量，為什么可以忽略呢？

我是這么理解的，本來這些帶△的量就是小信號，意思是圍繞一個中心值小范圍波動，所以帶△符號的量相對于不帶△符號的量是很小的。那么兩個都帶△符號的量相乘，乘積就更小了，所以干脆把它忽略掉了。

對于BUCK來說，只需要第一個式子就可以求出傳遞函數了，也就是下面這個

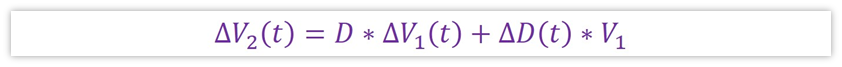
寫的有點長，我們回顧下我們最終的目的，我們的目的是要求出Gvd，也就是△Vo/△D的值，上面式子中，我們已經能知道△V2與△D的關系，那△V2與△Vo是什么關系呢？

回到我們Buck的拓撲

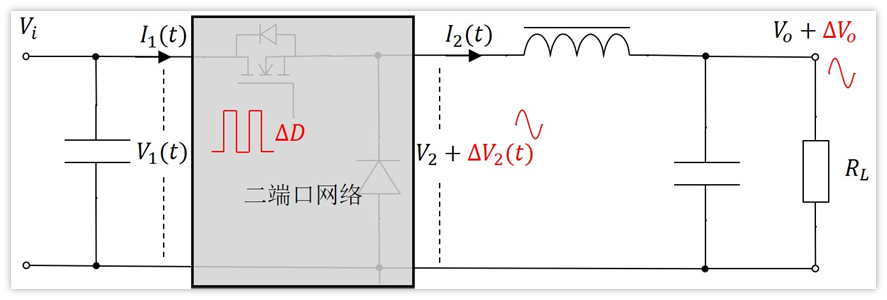
V1(t)不就是輸入信號Vi嗎？

理想情況下，Vi就是恒定的，占空比變化也不會導致Vi發生變化（不要考慮輸入的開關紋波，我們現在分析的是理想拓撲，輸入電源為理想電源，電壓就是恒定的）。

既然Vi恒定，那么V1(t)就恒定不變，那么前面說的V1(t)的變化量△V1(t)=0。所以上面的那個式子可以再次化簡下，如下：

另一方面，△V2指的是在占空比發生變化時，在電感前面引起的電壓的變化量。

我們知道了△V2，那么△Vo不就是后面電感L，電容C，負載R對△V2的分壓嗎？那么就有了：

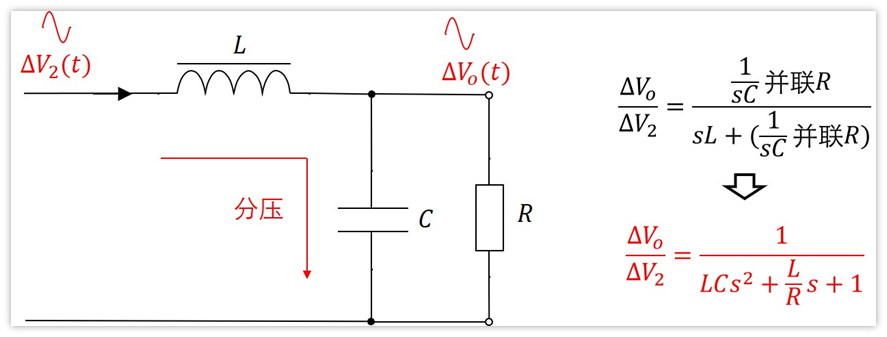
再結合前面得到的式子△V2=△D*Vi，我們就求得了最終的傳遞函數：

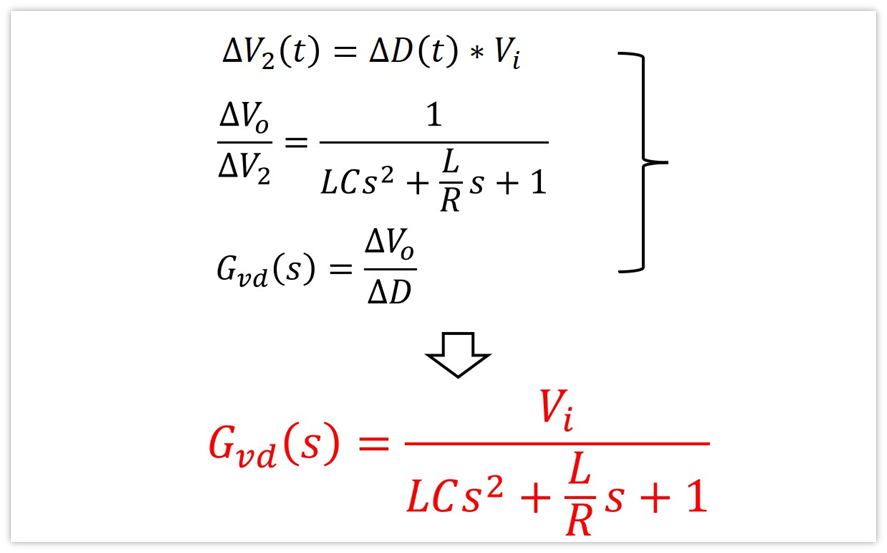
到此，我們就求出了buck的開關變換器的傳遞函數Gvd(s)。

寫到這里，我估計會有兄弟說：搞了一堆，我肉眼都能看出在電感之前的信號表達式△V2=△D*Vi，再把它后面的電感L，C，R看成是低通濾波器，1分鐘就能推出傳遞函數了。

確實如此，有點復雜，不過我上面的推導是普遍適用的法子，我拿BUCK來舉例其實不好。如果拿boost就比較好，因為boost肉眼看不出來，但用上面的法子就可以推導出來。

那下面就再看看Boost

Boost的CCM模式傳遞函數推導過程

有了前面的鋪墊，Boost我就寫簡單點，其實最關鍵的還是那個MOS和二極管，我們的過程依然是下面幾步。

1、二端口等效

2、端口參數關系，推導出兩個式子

3、代入電路，結合原理推導出傳遞函數

二端口等效

二端口等效如下：

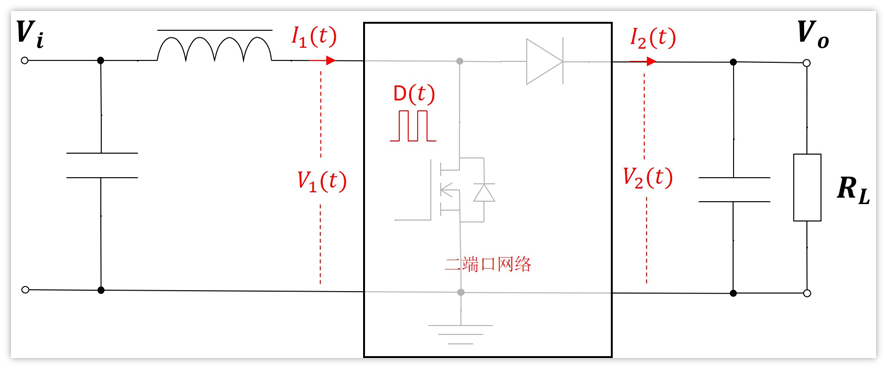
端口參數關系，推導出兩個式子

I1(t)，I2(t)，V1(t)，V2(t)為周期平均值，假如沒有任何干擾信號，它們和全時間的平均值是一樣的，每個周期都一樣，每個周期的平均值自然和全部時間內的平均值一樣，這應該沒毛病。

好，我們假設沒有干擾信號時，平均值分別是I1，I2，V1，V2，它們是個常量。此時開關信號的占空比也是恒定的，我們用D表示。

現在我們將干擾信號加進去，我們知道，系統只有滿足小信號條件的時候，才能將之近似看成線性系統。

既然干擾信號是小信號，那么這個干擾信號只會引起I1(t)，I2(t)，V1(t)，V2(t)隨時間小范圍變化，它們分別以I1，I2，V1，V2為中心進行波動，同理，占空比也會圍繞D為中心進行波動。

各變量的波動量不就是交流小信號嗎？

我們分別用符號△I1(t)，△I2(t)，△V1(t)，△V2(t)，△D(t)來表示。

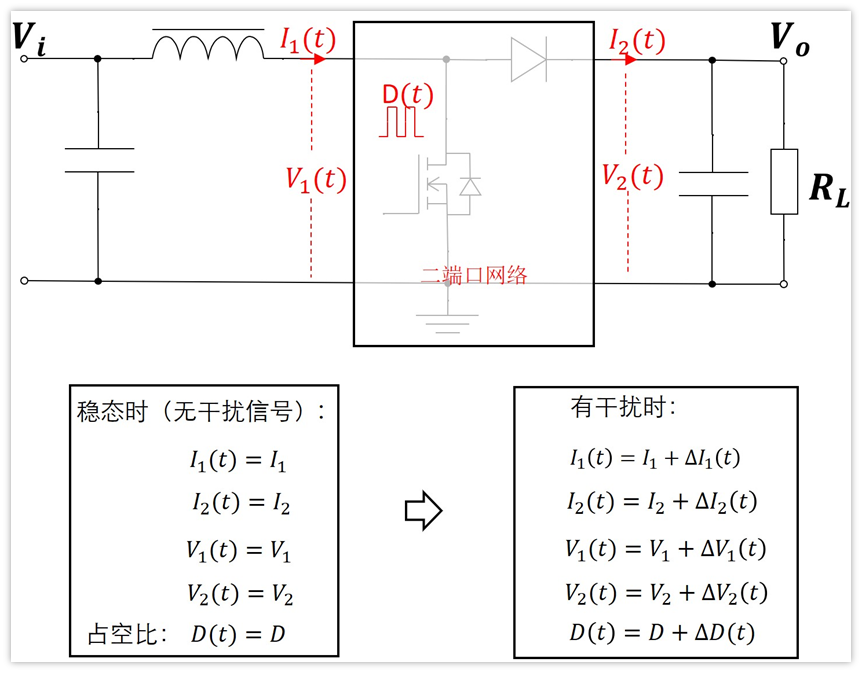
 式子已經列出來了，現在我們需要求他們之間的關系。

先看看V1(t)的物理意義，它是周期內的平均值。

顯然，V1(t)=V2(t)*(1-D(t))，為什么呢？

因為在MOS不導通的時候，二極管（看成理想二極管）導通，v1(t)為v2(t)，而在MOS導通的時候，v1(t)接GND，為0，所以，v1(t)在周期內的平均值V1(t)就等于不導通時間的百分占比乘以V2(t)，即：

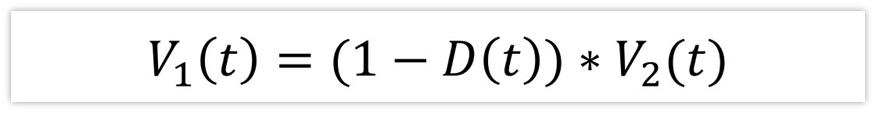
同樣的，I2(t)= I1(t)* (1-D(t))，那又是為什么呢？

因為MOS在不導通的時候，i2(t)等于i1(t)，而在MOS管導通的時候，i2(t)等于0，所以，i2(t)在周期內的平均值I2(t) 就等于不導通時間的百分占比乘以i1(t)，即：

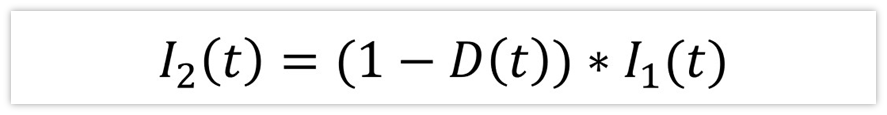
從推導過程看，上面兩個式子，無論是在穩態（沒有干擾），還是在有干擾的情況下，都是成立的。

小信號求解

我們把前面得到的幾個式子代換一下，就可以得到小信號的表達式。

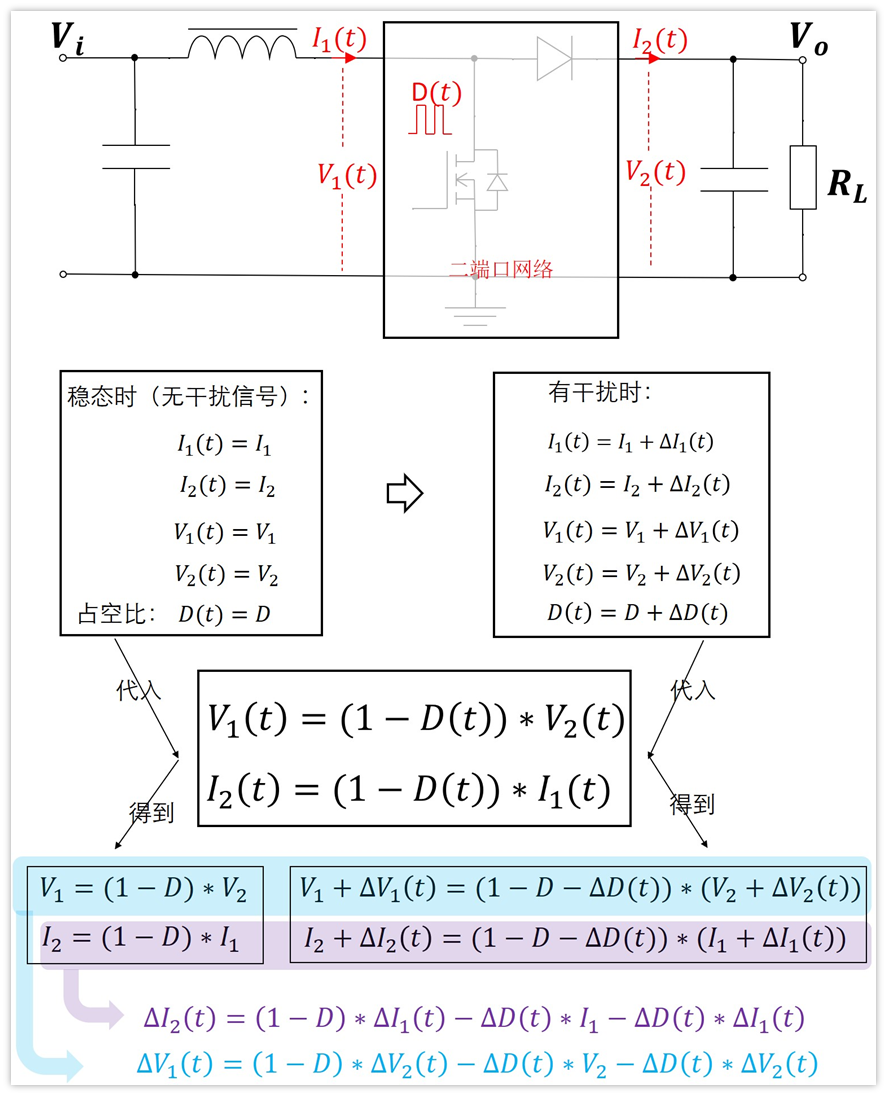
忽略高階小項，得到下面兩個小信號的式子：

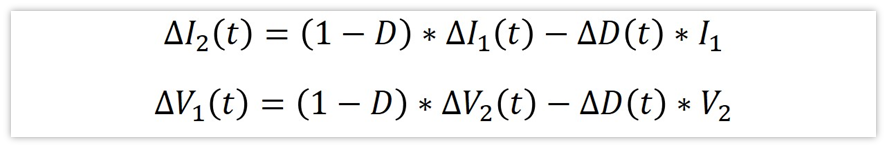
回想我們的目的，我們要得到傳遞函數，也就是需要知道△Vo與△D的比值關系。當然，我們會有一些量是已知的，比如輸入Vi，占空比D，還有電感L，負載阻抗R，負載濾波電容C，這些都是已知量。

回到Boost的拓撲

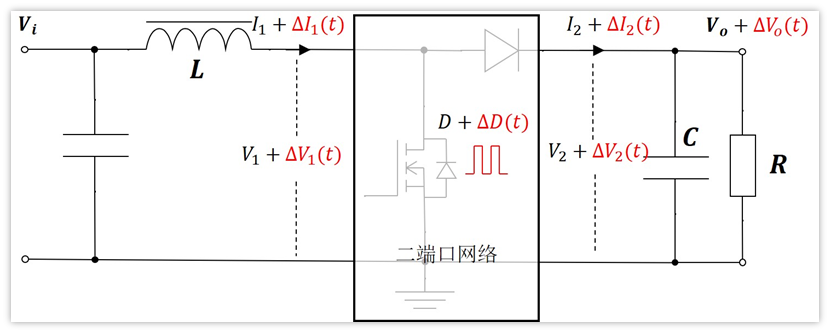
從上面我們能得到什么式子呢?

首先，在輸入端，對于交流小信號來說，輸入直流Vi相當于是短路，那么電感左邊相當于接地，根據復阻抗的歐姆定律，那么電感兩端壓降就是：sL*△I1(t)，也等于-△V1(t)，負號表示方向。

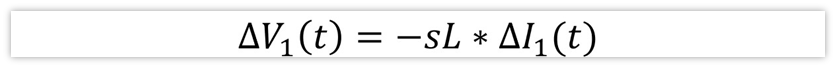
關于為什么“對于交流小信號來說，輸入直流Vi相當于是短路”的，我之前也寫過一篇文章，可以去瞅瞅。

其次，在輸出端，對于交流小信號來說，電壓△Vo=△V2，同時，根據復阻抗的歐姆定律，電壓等于電流乘以阻抗，即：

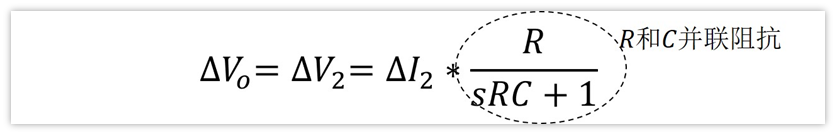
然后，V1為直流分量，因此有V1=Vi；

V2也為直流分量，因此有V2=Vo，I2=Vo/R

并且在小信號求解時，我們已經推出了兩個公式：

V1=(1-D)*V2；

I2=(1-D)*I1

我們把上述所有公式匯總，消除中間量，就可以求出傳遞函數了，如下圖：

以上就是boost求解傳遞函數的過程，看著是非常費勁，其實要是想通了就不難。

小結

很是費了一番功夫，最終求出了buck和boost的傳遞函數Gvd(s)。

我使用的方法其實就是《開關變換器的建模與控制+張衛平編著》里面的開關網絡平均值法，不過我結合自己的喜好，改造了下，沒有用變壓器等效，盡量用通俗的語言，一步一步推出公式來。

當然，我這么玩不太嚴謹，如果想要深入了解的兄弟，建議去看下這本書，里面有很多建模方法，非常的專業。

但是不好的地方就是也比較難懂，我來來回回看了好久，終于有些許領悟，能做到扔掉書本，自己推出buck和boost的開關變換器的傳遞函數了，過程就是上面寫的了。

以上內容其實在工作中是用不到的，各種拓撲的傳遞函數其實早已被前人給推導出來了，我們直接用就好。不過，人總有一些好奇心，會問個為什么，如果知道過程，那自然也是極好的。