獨家 | 在Python中使用廣義極端學生化偏差（GESD）進行異常檢測

作者：Shaleen Swarup

翻譯：歐陽錦

校對：王可汗

本文從理論和實踐角度介紹了使用廣義極端學生化偏差（GESD）進行異常檢測的方法，展示了Python代碼示例和相關源碼。

關鍵字：Python 異常值檢測 ESD

異常檢測在生活中起著非常重要的作用。通常，異常數據可能與某種問題或罕見事件有關，例如 ****欺詐、醫療問題、結構缺陷、設備故障等。這種聯系使得能夠挑選出哪些數據點可以被視為異常值是非常有趣的，因為從商業角度識別這些事件通常是十分有趣的事情。

此外，許多統計方法對異常值的存在很敏感。例如，平均值和標準差的計算可能會被單個嚴重不準確的數據點所影響。檢查異常值應該是任何數據分析的常規部分，并且應該檢查潛在的異常值以查看它們是否可能是錯誤的數據。

什么是異常值檢測

任何發現數據集異常值的過程都可以被稱為異常檢測；也就是檢測那些不合群的事物。這些異常可能是異常的網絡流量，fritz上的一個傳感器，或者只是分析前識別要清理的數據。

清理的數據

https://www.bmc.com/blogs/data-normalization/

基于不同方案或方法的多種技術可以用來識別異常。例如，圖形的方法（箱線圖、散點圖）；基于距離的方案（最近鄰算法、聚類算法）；統計方法（GESD、基于四分位數的技術）等等。每種方案都有其優缺點，其效果都取決于實際用例。

在本文中，我們將重點關注GESD（廣義極端學生化偏差）并在Python中實現一個簡單的示例以更好地了解它的原理。在開始之前，我想說明，這篇文章深受我的探索性數據分析教授Edward McFowland和Bhavesh Bhatt在YouTube上的機器學習和統計教程的講座的啟發。

機器學習和統計教程

https://www.youtube.com/channel/UC8ofcOdHNINiPrBA9D59Vaw

什么是廣義極端學生化偏差（Generalized Extreme Studentized Deviate）

GESD是一種簡單的統計方法，用于檢測遵循近似正態分布的單變量數據集中的一個或多個異常值。統計方法假設常規數據遵循某種統計模型（或分布），而不遵循模型（或分布）的數據則是異常值。

GESD克服了Grubbs檢驗和Tietjen-Moore檢驗的主要限制：即必須明確確定疑似異常值的數量k。如果沒有正確指定k，則可能會擾亂這些測試的結論。而GESD測試只要求確定疑似異常值數量的上限。

給定上限r，GESD測試基本上執行r個單獨的測試：一個異常值的測試，兩個異常值的測試，依此類推直到r個異常值。

GESD測試定義在以下假設上：

H0：數據集中沒有異常值

Ha：數據集中最多有r個異常值

GESM的檢驗統計量公式如下：

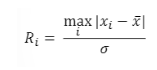
GESD的檢驗統計量

這里，x_bar和σ分別表示樣本均值和樣本標準差。

在GESD中，我們刪去使得 | xi - x_bar | 最大化的觀測值。然后，用n-1個觀察值重新計算上述統計量。我們重復這個過程，直到r個觀測值被移除。我們由此得到r統計量R1, R2 ……, Rr。通過代碼示例，這個過程將變得更加清晰。

對應于r檢驗統計量，由以下公式計算r的臨界值：

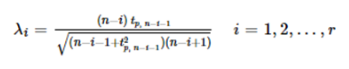
臨界值計算

其中 tp, ν 是具有ν自由度的t分布的100p百分點，并且

t分布

https://www.itl.nist.gov/div898/handbook/eda/section3/eda3664.htm

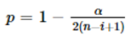
我們的顯著性水平將用α表示。

異常值的數量是通過找到能滿足Ri > λi的最大的i來確定的。

Rosner的模擬研究表明，該近似臨界值對于樣本數量n ≥ 25非常準確，對于n ≥ 15也相當準確。

請注意，盡管GESD本質上是依序使用Grubbs測試而實現的，但仍有一些重要區別：

Grubbs測試

https://www.itl.nist.gov/div898/handbook/eda/section3/eda35h1.htm

GESD測試會根據被測試的異常值的數量對臨界值進行適當的調整，而依序使用Grubbs測試的則沒有這樣的調整。

如果遮蔽效應明顯，Grubbs 測試的依次使用可能會過早停止。

現在再鞏固一下理論部分，在Python中實現GESD以了解它的實際工作原理吧。

首先，模擬我們的數據。這里我們創建了0到1之間的100個隨機值。數據的散點圖如下所示。

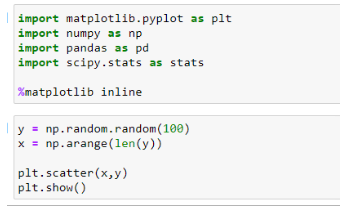
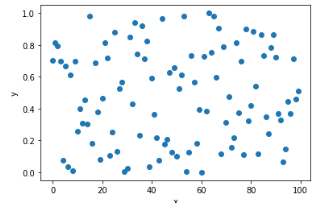
現在，我們特意在數據中放入一些異常值進行識別。

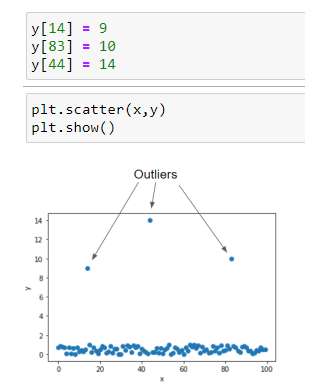
有異常值的數據

現在我們將創建單獨的函數來計算檢驗統計量和臨界值。

計算檢驗統計量的函數如下：

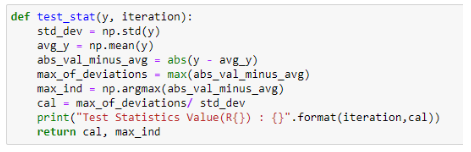
計算臨界值的函數如下：

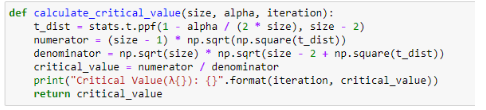
下面這個函數將所有內容匯總在一起并執行r次以識別異常值的數量。對于每次迭代，我們使用上面的函數來計算使得|xi - x_bar| 最大化的檢驗統計量，并計算其相應的臨界值，然后從我們的數據中刪除這個觀測值以進行下一次迭代。

在我們的數據上以5%的顯著性水平和具有7個異常值上限的情況調用這個函數會產生以下結果：

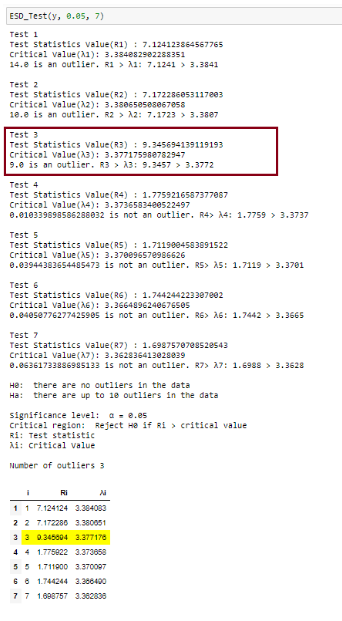
可以看到一共進行了7次檢驗。異常值的數量是通過找到滿足Ri > λi的最大的i來確定的。對于此示例，檢驗統計量大于臨界值（在顯著性水平為5%時）的最大異常值數為3。因此，我們得出結論，該數據集中有3個異常值。

代碼鏈接：

https://gist.github.com/shaleenswarup/77c711ac5bade7c8735fd309d94348ef#file-gistfile1-py

這就是Python中使用GESD進行異常檢測的實現。希望本文對您實現這種在數據中查找異常值的簡單而有效的方法有所幫助。想查看更多項目，請查看作者的 Github 個人資料。

作者的 Github 個人資料

https://github.com/shaleenswarup

引用

1. bmc | Anomaly Detection with Machine Learning: An Introduction by Jonathan Johnson

2. Anomaly detection using PCA from datascience904

https://datascience904.wordpress.com/2019/10/14/anomaly-detection-using-pca/

3. Generalized ESD Test for Outliers from Engineering Statistics

https://www.itl.nist.gov/div898/handbook/eda/section3/eda35h3.htm

原文標題：

Anomaly Detection with GESD (Generalized Extreme Studentized Deviate) in Python

原文鏈接：

https://towardsdatascience.com/anomaly-detection-with-generalized-extreme-studentized-deviate-in-python-f350075900e2