獨家 | Python的“predict_prob”方法不能真實反映預測概率校準(如何實現校準)
作者: Samuele Mazzanti
翻譯:歐陽錦
校對:王可汗
圖源自作者
數據科學家通常根據準確性或準確性來評估其預測模型,但幾乎不會問自己:
“我的模型能夠預測實際概率嗎?”
但是,從商業的角度來看,準確的概率估計是非常有價值的(準確的概率估計有時甚至比好的精度更有價值)。來看一個例子。
想象一下,你的公司正在出售2個杯子,一個是普通的白色杯子,而另一個則上面印有小貓的照片。你必須決定向這位給定的客戶展示哪個杯子。為此,你需要預測給定的用戶購買每個杯子的可能性。因此,你訓練了幾個不同的模型,你會得到以下結果:
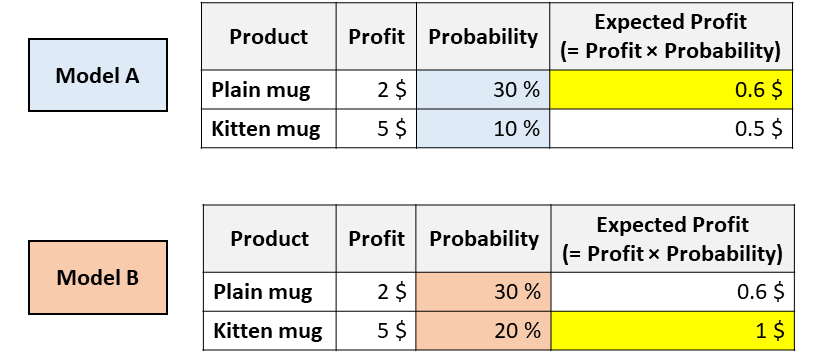
具有相同ROC(receiver operating characteristic)但校準不同的模型。[圖源自作者]
現在,你會向該用戶推薦哪個杯子?
以上兩種模型都認為用戶更有可能購買普通馬克杯(因此,模型A和模型B在ROC曲線下具有相同的面積,因為這個指標僅僅對分類進行評估)。
但是,根據模型A,你可以通過推薦普通馬克杯來最大化預期的利潤,然而根據模型B,小貓馬克杯可以最大化預期的利潤。
在像這樣的現實應用中,搞清楚哪種模型能夠估算出更好的概率是至關重要的事情。
在本文中,我們將了解如何度量概率的校準(包括視覺和數字),以及如何“糾正”現有模型以獲得更好的概率。
“predict_proba”的問題
Python中所有最流行的機器學習庫都有一種稱為“ predict_proba”的方法:Scikit-learn(例如LogisticRegression,SVC,RandomForest等),XGBoost,LightGBM,CatBoost,Keras…
但是,盡管它的名字是預測概率,“predict_proba”并不能完全預測概率。實際上,不同的研究(尤其是這個研究和這個研究)表明,最為常見的預測模型并沒有進行校準。
數值在0與1之間不代表它就是概率!
但是,什么時候可以說一個數值實際上代表概率呢?
想象一下,你已經訓練了一種預測模型來預測患者是否會患上癌癥。如果對于給定的患者,模型預測的概率為5%。原則上,我們應該在多個平行宇宙中觀察同一位患者,并查看其實際上患上癌癥的頻率是否為5%。
但是這種觀察條件這是不可能發生的事,所以最好的替代方法是將所有概率在5%附近的患者都接受治療,并計算其中有多少人真的患了癌癥。如果觀察到的患癌百分比實際上接近5%,則可以說該模型提供的概率是“已校準”的。
當預測的概率反映了真實情況的潛在概率時,這些預測概率被稱為“已校準”。
那么,如何檢查一個模型是否已校準?
校準曲線
評估一個模型校準的最簡單的方法是通過一個稱為“校準曲線”的圖(也稱為“可靠性圖”,reliability diagram)。
這個方法主要是將觀察到的結果通過概率劃分為幾類(bin)。因此,屬于同一類的觀測值具有相近的概率。在這一點上,對于每個類,校準曲線將預測這個類的平均值(即預測概率的平均值),然后將預測概率的平均值與理論平均值(即觀察到的目標變量的平均值)進行比較。
Scikit-learn通過“ calibration_curve”函數可以完成所有這些工作:

你只需要確定類的數量和以下兩者之間的分類策略(可選)即可:
“uniform”,一個0-1的間隔被分為n_bins個類,它們都具有相同的寬度;
“quantile”,類的邊緣被定義,從而使得每個類都具有相同數量的觀測值。
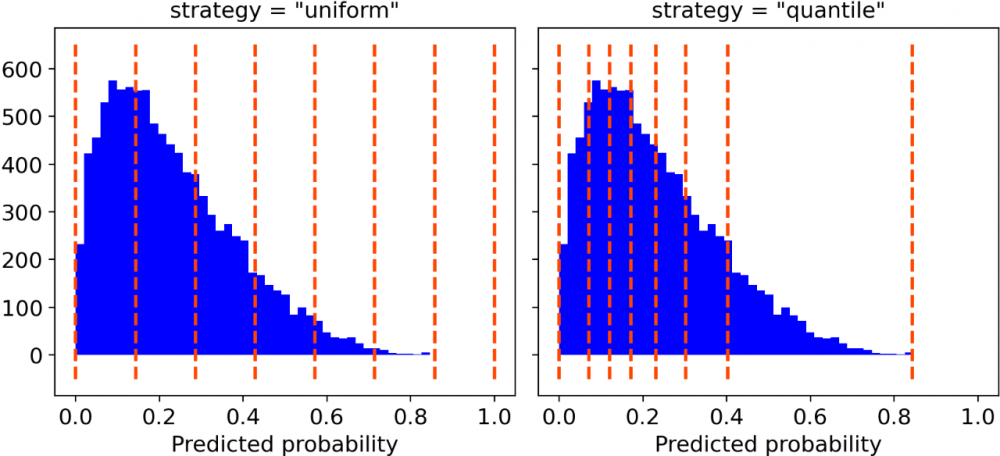
分類策略,分類數量為7。[圖源自作者]
出于繪圖目的,本人更喜歡“quantile”的分類策略。實際上,“uniform”分類可能會引起誤導,因為有些類中可能只包含很少的觀察結果。
Numpy函數給每個分類返回兩個數組,每個數組包含平均概率和目標變量的平均值。因此,接下來要做的就是繪制它們:

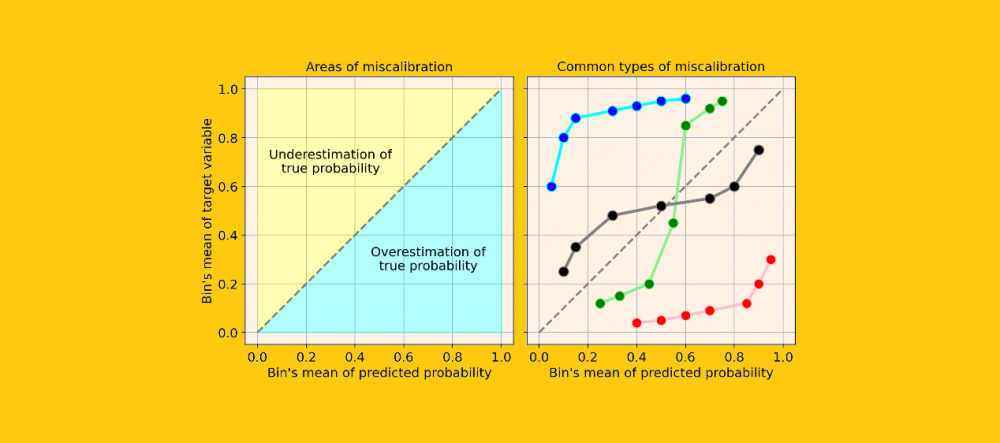
假設你的模型具有良好的精度,則校準曲線將單調增加。但這并不意味著模型已被正確校準。實際上,只有在校準曲線非常接近等分線時(即下圖中的灰色虛線),您的模型才能得到很好的校準,因為這將意味著預測概率基本上接近理論概率。
讓我們看一些校準曲線的常見類型的例子,它們表明了模型的校準錯誤:
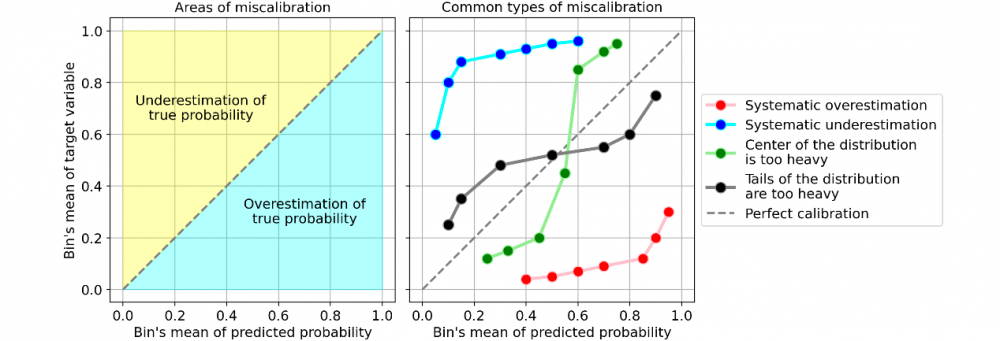
錯誤校準的常見示例。 [圖源自作者]
最常見的錯誤校準類型為:
系統高估。與真實分布相比,預測概率的分布整體偏右。當您在正數極少的不平衡數據集上訓練模型時,這種錯誤校準很常見。(如紅線)
系統低估。與真實分布相比,預測概率的分布整體偏左。(如藍線)
分布中心太重。當“支持向量機和提升樹之類的算法趨向于將預測概率推離0和1”(引自《Predicting good probabilities with supervised learning》)時,就會發生這類錯誤校準。(如綠線)
分布的尾巴太重。例如,“其他方法(如樸素貝葉斯)具有相反的偏差(bias),并且傾向于將預測概率趨近于0和1”(引自《Predicting good probabilities with supervised learning》)。(如黑線)
如何解決校準錯誤(Python)
假設你已經訓練了一個分類器,該分類器會產生準確但未經校準的概率。概率校準的思想是建立第二個模型(稱為校準器),校準器模型能夠將你訓練的分類器“校準”為實際概率。
請注意,用于訓練的第一個分類器的數據不能被用于校準。
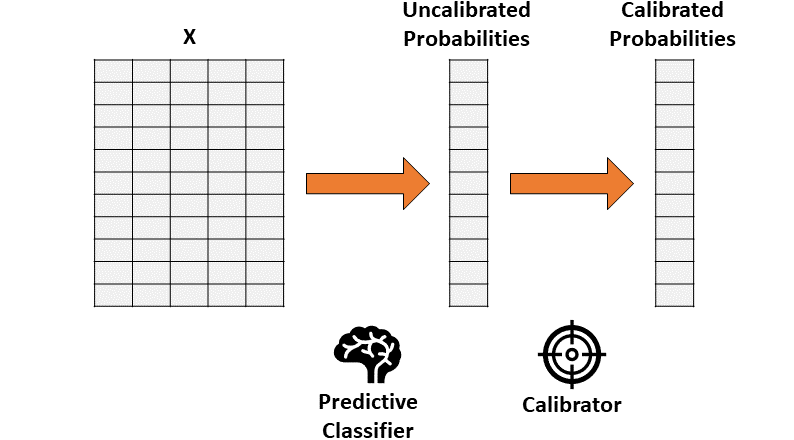
通過兩步法進行概率校準。 [圖源自作者]
因此,校準包括了將一個一維矢量(未校準概率)轉換為另一個一維矢量(已校準概率)的功能。
兩種常被用作校準器的方法:
保序回歸。一種非參數算法,這種非參數算法將非遞減的自由格式行擬合到數據中。行不會減少這一事實是很重要的,因為它遵從原始排序。
邏輯回歸。
看看使用Python如何在玩具數據集中實際應用校準器:
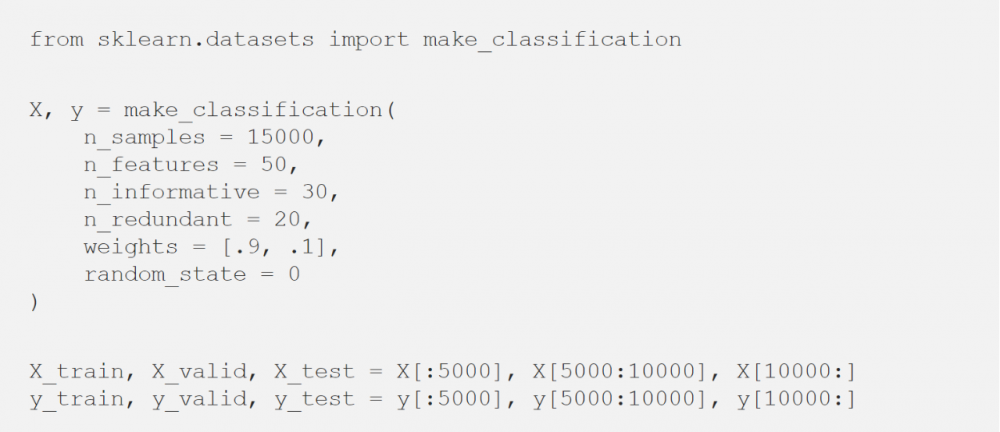
首先,需要擬合一個分類器。這里使用隨機森林(或者任何具有“predict_proba”方法的模型都可以)。

然后,使用分類器的輸出(在驗證數據集上)來擬合校準器,并最終預測測試數據集的概率。
保序回歸

邏輯回歸
現在有三種選擇來預測概率:
1. 普通隨機森林,
2. 隨機森林 + 保序回歸,
3. 隨機森林 + 邏輯回歸。
但是,我們如何評估最校準的是哪一個呢?
量化校準錯誤
每個人都喜歡圖片展示的量化效果。但是除了校準圖外,我們還需要一種定量的方法來測量校準。最常用的方法稱為“預期校準誤差(Expected Calibration Error)”,這個方法回答了下面的問題:
我們模型的預測概率與真實概率平均相距多遠?
以一個分類器為例:
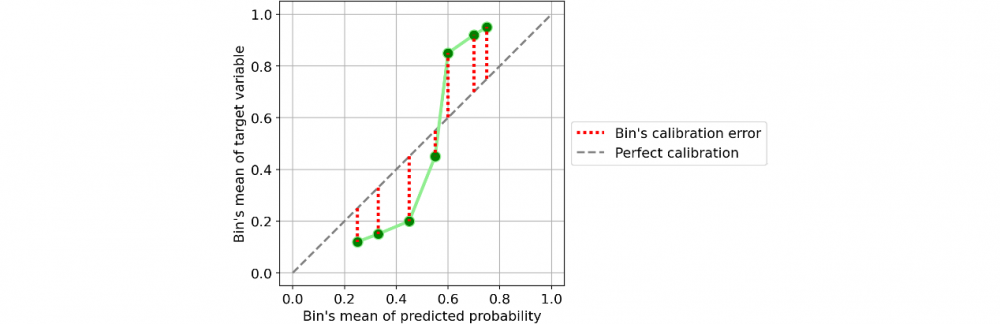
對單個類別(bin)的校準。[圖源自作者]
定義單個類別(bin)的校準誤差很容易:即為預測概率的平均值與同一類別(bin)內的正數所占百分比的絕對差值。
如果考慮一下這個定義,它非常直觀且符合邏輯。取一個類別(bin),并假設其預測概率的平均值為25%。因此,我們預計該類別中的正數所占百分比大約等于25%。如果這個百分比離25%越遠,意味著這個類別(bin)的校準就越差。
因此,預期校準誤差(Expected Calibration Error, ECE)是單個類別的校準誤差的加權平均值,其中每個類別的權重與它包含的觀測值的數量成正比:
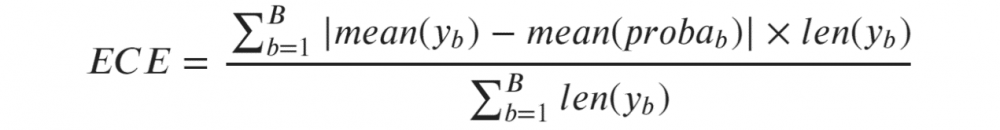
預期校準誤差(ECE)[圖源自作者]
其中b標識一個類別(bin),B是類別(bin)的數量。注意,分母只是樣本總數。
但是這個公式給我們留下了定義B值(即,類別數量)的問題。為了找到盡可能中性的指標,我建議根據Freedman-Diaconis rule(這是一個統計規則,旨在找到使直方圖盡可能接近理論概率分布的B值。)
在Python中使用Freedman-Diaconis rule非常簡單,因為它已經在numpy的直方圖函數中被實現(足以將字符串“ fd”傳遞給參數“ bins”)。
以下是預期校準錯誤(ECE)的Python實現,默認情況下采用Freedman-Diaconis rule:
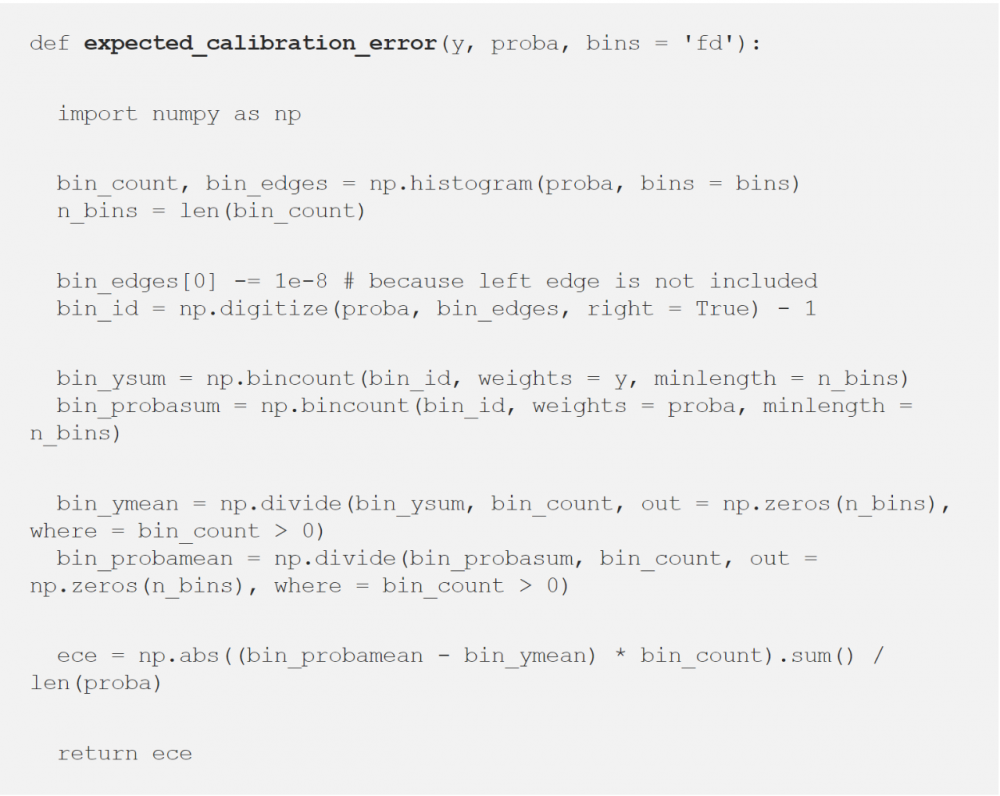
現在,我們有了一個校準方法,讓我們比較上面獲得的三個預測概率的模型(在測試集上)的校準情況:

三個模型的ECE比較。 [圖源自作者]
正如上圖所示,如果你認為普通隨機森林的ECE為7%,那么保序回歸在校準方面則提供了最好的結果,這可以看作是一個巨大的進步,因為平均來看,使用保序回歸的模型,其預測概率距離真實概率只有1.2%。
引用
如果你想了解更多概率校準的主題,以下是一些有趣的文章(本文的基石):
?Predicting good probabilities with supervised learning? (2005) by Caruana and Niculescu-Mizil.
?On Calibration of Modern Neural Networks? (2017) by Guo et al.
?Obtaining Well Calibrated Probabilities Using Bayesian Binning? (2015) by Naeini et al.
原文標題:
Python’s ?predict_proba? Doesn’t Actually Predict Probabilities (and How to Fix It)
原文鏈接:
https://towardsdatascience.com/pythons-predict-proba-doesn-t-actually-predict-probabilities-and-how-to-fix-it-f582c21d63fc
*博客內容為網友個人發布,僅代表博主個人觀點,如有侵權請聯系工作人員刪除。
加速度計相關文章:加速度計原理


