騰訊AI Lab聯(lián)合清華、港中文，萬(wàn)字解讀圖深度學(xué)習(xí)歷史、最新進(jìn)展與應(yīng)用（2）

二、圖神經(jīng)網(wǎng)絡(luò)的研究進(jìn)展

了解了 GNN 的基本知識(shí)和發(fā)展脈絡(luò)，接下來(lái)我們將踏入當(dāng)前的前沿研究領(lǐng)域，解讀近期的一些理論研究成果和設(shè)計(jì)創(chuàng)新。

1.圖神經(jīng)網(wǎng)絡(luò)的表達(dá)能力

我們知道圖在表達(dá)事物的關(guān)系方面能力非凡，但圖神經(jīng)網(wǎng)絡(luò)表達(dá)能力的極限在哪里？清華大學(xué)計(jì)算機(jī)系助理研究員、清華大學(xué)「水木學(xué)者」、騰訊「犀牛鳥(niǎo)訪問(wèn)學(xué)者」黃文炳在課程中介紹了相關(guān)的研究進(jìn)展。

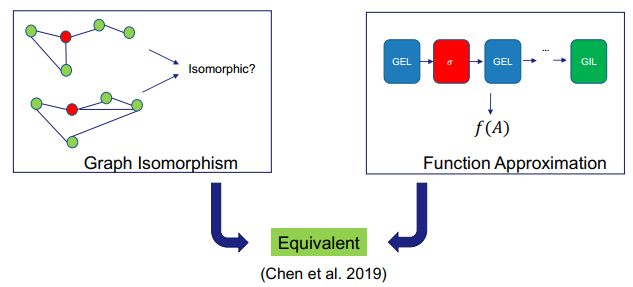
為了有效地評(píng)估 GNN 的表達(dá)能力，首先需要定義評(píng)估標(biāo)準(zhǔn)。目前來(lái)說(shuō)，可通過(guò)三種典型任務(wù)來(lái)進(jìn)行評(píng)估：圖同構(gòu)、函數(shù)近似和圖檢測(cè)/優(yōu)化/評(píng)估。

對(duì)于圖同構(gòu)任務(wù)，GNN 的目標(biāo)是確定任意給定的兩個(gè)圖是否同構(gòu)。這是一個(gè)很重要的任務(wù)。對(duì)于圖分類任務(wù)而言，如果兩個(gè)圖是同構(gòu)的，則 GNN 需要為這兩個(gè)圖輸出同樣的標(biāo)簽。

但是，判定圖是否同構(gòu)的問(wèn)題是一個(gè) NP-hard 問(wèn)題，傳統(tǒng)的 Weisfeiler-Lehman（WL）測(cè)試方法除了少數(shù)圖結(jié)構(gòu)外，基本能否識(shí)別大多數(shù)圖結(jié)構(gòu)是否同構(gòu)。而 GNN 能更好地解決這一問(wèn)題嗎？

并不一定。2019 年，Xu et al. 和 Morris et al. 已經(jīng)證明 GNN 至多做到與 WL 測(cè)試一樣強(qiáng)大。之后，Xu et al. 還進(jìn)一步證明，如果 GNN 中的聚合和讀出函數(shù)（readout function）是單射函數(shù)，則 GNN 就與 WL 測(cè)試等效。

對(duì)于函數(shù)近似任務(wù)，該任務(wù)的目標(biāo)是判斷 GNN 能否以任意準(zhǔn)確度近似任何基于圖的函數(shù)。因?yàn)?GNN 本身也是基于圖的某種函數(shù)，因此 GNN 在這一任務(wù)上的表現(xiàn)將能體現(xiàn)其能力。實(shí)際上，DNN 也有類似的評(píng)估任務(wù)。我們知道，只要隱藏單元足夠多，DNN 可以收斂到任何向量函數(shù)，這就是所謂的「通用近似定理」。所以我們很自然也會(huì)為 GNN 提出類似的問(wèn)題。

Maron et al. 提出了一種架構(gòu)，對(duì)于擁有圖不變映射層（graph invariant layer）和圖等變映射層（graph equivariant layer）的 GNN，如果在一個(gè)非線性層（比如 ReLU）之后堆疊等變映射層，層層疊加，然后在最后添加圖不變映射層。可以看出這樣的模型能在輸入的排列方式變化時(shí)保持映射不變性。這樣的模型被稱為圖不變網(wǎng)絡(luò)（INN）。

INN 有多強(qiáng)大？Maron et al. 證明對(duì)于任意連續(xù)的不變式圖函數(shù)，如果某些條件成立，我們可以找到特定的 INN 參數(shù)，使其能以任意精度估計(jì)該函數(shù)。這是圖學(xué)習(xí)領(lǐng)域一大強(qiáng)有力的理論結(jié)果。對(duì) GNN 而言，這就相當(dāng)于對(duì) DNN 而言的通用近似定理。

看過(guò)了圖同構(gòu)和函數(shù)近似的近期進(jìn)展，更進(jìn)一步，這兩者之間又有何關(guān)系呢？Chen et al. 2019 證明在滿足一些條件的情況下，這兩者其實(shí)是等效的。

接下來(lái)，我們看看 GNN 是否有足夠的表達(dá)能力來(lái)解決更困難的任務(wù)，比如尋找圖中的最短路徑或確定圖中是否存在環(huán)。這些任務(wù)的難度很高，因?yàn)樗鼈冃枰诠?jié)點(diǎn)層面執(zhí)行很細(xì)粒度的推理。

Loukas 證明 GNN 能解決這些任務(wù)，他得出結(jié)論：只要 GNN 的深度和寬度足夠，而且節(jié)點(diǎn)之間具有可互相判別的屬性，則 GNN 就能完成這些任務(wù)。這里深度是指 GNN 的層數(shù)，寬度則是指隱藏單元的維度。

因此，總結(jié)起來(lái)，只要架構(gòu)合適，GNN 其實(shí)具有非常強(qiáng)大的表達(dá)能力；也因此，要充分發(fā)掘 GNN 的真正實(shí)力，我們還需要更多架構(gòu)方面的研究探索。

2.訓(xùn)練深度圖神經(jīng)網(wǎng)絡(luò)

前面已經(jīng)簡(jiǎn)單提到，深度對(duì) GNN 的能力而言是非常重要的。這一點(diǎn)在深度神經(jīng)網(wǎng)絡(luò)（DNN）上也有體現(xiàn)——更深的網(wǎng)絡(luò)往往具有強(qiáng)大的表達(dá)能力，可以說(shuō)深度網(wǎng)絡(luò)就是當(dāng)前的人工智能發(fā)展熱潮的最主要驅(qū)動(dòng)力之一。

那么，具體來(lái)說(shuō)，更深度的 GNN 是否也有如此的優(yōu)勢(shì)呢？更深度的 GNN 能否像 CNN 一樣獲得更大的感受野？

答案當(dāng)然是肯定的。舉個(gè)例子，尋找最短路徑問(wèn)題需要非常深的感受野來(lái)尋找所有可能的路徑，環(huán)檢測(cè)和子圖查找問(wèn)題也都需要較大的感受野。

那么，我們可以怎樣增大 GNN 的感受野，使其具備更強(qiáng)大的能力呢？為此，我們需要更深或更寬的 GNN。

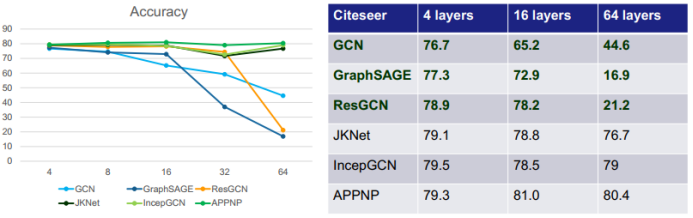
首先來(lái)看通過(guò)簡(jiǎn)單增加深度來(lái)擴(kuò)展 GNN 的方法。可以看到，對(duì)于下圖中的六種 GNN：GCN、GraphSAGE（進(jìn)一步改進(jìn)了池化方法）、ResGCN（使用了殘差網(wǎng)絡(luò)的思路）、JKNet（使用了 DenseNet 的思路）、IncepGCN（使用了 Inception-v3 的思路）、APPNP（借用了 PageRank 的思路），簡(jiǎn)單增加深度并不一定能提升準(zhǔn)確度，甚至還可能出現(xiàn)相反的狀況，比如 GCN、GraphSAGE 和 ResGCN 在深度增大時(shí)準(zhǔn)確度反而顯著下降。

這不禁讓人疑問(wèn)：增加深度能提升表達(dá)能力的根本原因是什么？又是什么原因阻礙了 GNN 的深度擴(kuò)展？

近期的研究找到了有礙 GNN 變得更深的三大根本原因：過(guò)平滑（over-smoothing）、過(guò)擬合（overfitting）和訓(xùn)練動(dòng)態(tài)變化（training dynamics）。其中后兩者也是常見(jiàn)的深度學(xué)習(xí)問(wèn)題，而過(guò)平滑則是圖深度學(xué)習(xí)方面特有的問(wèn)題。