基于多特征SVMs分類器的手語識別*
作者：楊全 西安文理學(xué)院 計算機(jī)科學(xué)系 彭進(jìn)業(yè) 西北大學(xué) 信息科學(xué)與技術(shù)學(xué)院
時間：2009-04-14
來源：電子產(chǎn)品世界
收藏
加入技術(shù)交流群
掃碼加入
和技術(shù)大咖面對面交流
海量資料庫查詢
SVMs的主要思想是建立一個超平面作為決策曲面，使得正例和反例之間的隔離邊緣被最大化。對于二維線性可分情況，令 H為把兩類訓(xùn)練樣本沒有錯誤地分開的分類線，H1，H2分別為過各類中離分類線最近的樣本且平行于分類線的直線，它們之間的距離叫做分類間隔。所謂最優(yōu)分類線就是要求分類線不但能將兩類正確分開，而且使分類間隔最大。在高維空間，最優(yōu)分類線就成為最優(yōu)分類面[8，9]。
設(shè)線性可分樣本集為(xi,yi))，i=1,2,…,n,x∈Rd，即x是d維特征向量，y∈{+1,-1}是類別標(biāo)號，d維空間線性判斷函數(shù)的一般形式為g(x)=w×x+b，分類面方程為：w×x+b=0 (1)
式中w為權(quán)向量，b為分類閾值。要求分類面對所有樣本正確分類，就是要求它滿足：
Yi[w×xi+b]-1≥0,i=1,2,…,n (2)
滿足上述條件且使||w||2最小的分類面就叫做最優(yōu)分類面， H1，H2上的訓(xùn)練樣本點(diǎn)，也就是使式(2)中等號成立的樣本點(diǎn)，稱作支持向量。解這個最優(yōu)化問題后得到的最優(yōu)分類函數(shù)是：
在學(xué)習(xí)樣本是線性不可分，但卻是非線性可分的情況下，可以通過非線性變換把學(xué)習(xí)樣本變換到高維空間，使其在高維空間里是線性可分的。用核函數(shù) K(x,y)代替原來的點(diǎn)積(x·y)，Mercer定理指出，核函數(shù) K(x,y)通過與其相聯(lián)系的非線性變換Φ隱含地把特征向量映射到高維特征空間，使得學(xué)習(xí)樣本成為線性可分的。常用的核函數(shù)有:
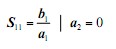
評論