晶閘管控制串聯電容器應用于彈性交流輸電系統的穩定度分析
摘要:彈性交流輸電系統設備,如晶閘管控制串聯電容器(TCSC)、制動電阻、并聯電容電抗與靜態移相器被用來動態調整網絡配置,以提高系統的靜態特性和暫態穩定度。現代電力系統龐大而復雜,擾動常改變電網結構并導致非線性響應。本文采用晶閘管控制串聯電容器提高電力系統動態穩定度,晶閘管控制串聯電容器的阻抗由輔助進相-遲相控制器根據發電機速度偏差進行調整,輔助控制器參數由基于模態控制理論的極點指定法來確定。針對指定的操作點設計控制器,探討系統在不同加載條件下,不同功率因數,端電壓下的閉環特征值靈敏度。并對具有輔助進相-遲相控制器的晶閘管控制串聯電容進行檢測,以保證電力系統在各運行點的阻尼特性。數值模擬結果表明提出的控制能有效的提高大信號瞬態穩定度和電力傳輸能力。
本文引用地址:http://www.104case.com/article/284994.htm傳統交流輸電網的電流潮流屬于自然分布狀態,不易控制電流流向。在并聯的網路中,當某條線路輸送功率改變時,會導致同一并聯電路輸送電力的改變或導致環流。若傳輸功率增加時,會造成動態穩定度的惡化或電壓崩潰。彈性交流輸電系統是指在傳統交流輸電系統中,引入電力電子技術,提高電網的運行效率。通過引入可控大功率電子元件,使輸電網的阻抗、相角可控,使電網功率潮流分布可控,直接控制有功功率和無功功率的傳輸,提高系統應對緊急事故的靈活性,提高現有輸電設備的傳輸能力和系統穩定度[1-3]。
彈性交流輸電系統具有以下優點:(1)電力潮流可彈性控制;(2)輸電能力可大幅提高;(3)防止設備與系統故障的累積,避免連鎖效應;(4)提升區域間電能傳輸能力,充分利用發電容量;(5)根據系統需求提供快速靈活補償,改善供電品質;(6)抑制電力系統振蕩。彈性交流輸電系統設備,如并聯電容電抗、晶閘管控制制動器、靜態同步調相器、靜態移相器與晶閘管控制串聯電容器被用于調整動態網路,以加強系統靜態特性與暫態穩定度。對于長距離輸電線路,為避免壓降過大,常使用晶閘管控制串聯電容器提高線路輸電能力[4-5] 。
本文在模態控制理論的基礎上提出的極點指定法來確定彈性交流輸電系統控制器的設計法則,提高控制器適應性以滿足電力系統復雜、高度非線性及狀態多變的使用特性。
1 晶閘管控制串聯電容器
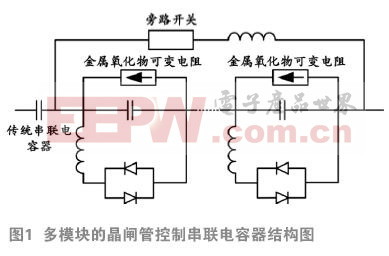
多模塊的晶閘管控制串聯電容器的結構如圖1所示。單個TCSC模塊由一個串聯電容器并聯一個晶閘管控制器,為了防止過電壓,還會并聯一個金屬氧化物可變電阻。一個完整的補償系統由多個模塊串聯而成,并且有一個旁路開關,在TCSC故障或維修時將其旁路掉[6-7] 。
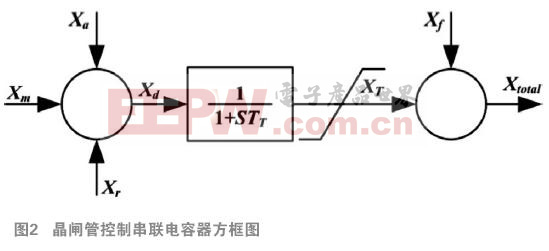
TCSC方框圖如圖2所示,其中Xa為開環輔助信號,如電力潮流控制信號;Xr為TCSC的初始操作點,Xm為調制小信號輸入,上述三個信號合成TCSC的控制信號Xd。TCSC的自然響應延遲為時間的單一函數,用TT表示;TCSC的輸出等效阻抗受操作模式與容量而存在上下限XTmax和XTmin;XT與固定電容Xf合成Xtotal。
由TCSC方框圖得到1階微分方程式:
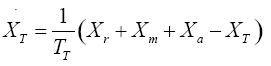 (1)
(1)
TCSC的初始操作點Xr可由系統操作點Xtotal反推得到:
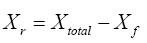 (2)
(2)
2 電力系統模型
當電力系統有小負載變動或系統本身發生自發性低頻振蕩時的動態行為,即小信號穩定度。低頻振蕩現象是一種轉軸的動態行為,其頻率大約在0.5 Hz~2Hz之間,可用線性系統中的頻域特征值來分析。
全部的特征值涵蓋的頻率范圍很廣,其中對應的低頻振蕩部分稱為系統機電模式。系統低頻振蕩常導致系統運轉困難,嚴重的可引起系統停機等穩定度問題。
電力系統發生振蕩時,若系統有足夠的阻尼時,在干擾解除后發電機可迅速恢復到穩定狀態。改善穩定度的方法有在靜態勵磁機系統中外加電力系統穩定器,設計良好的調速器和汽輪機控制器。調整靜態功率補償器的虛功率,并聯電抗器和靜態移相器,以提高系統的阻尼,提高穩定度。
隨著大功率電子元件的快速發展,晶閘管控制串聯電容器能有效提升電網的輸電效率,增加系統的穩定度。典型的單機無限匯流排電力系統如圖3所示,勵磁系統采用如圖4所示的IEEE Type1勵磁機,發電機的非線性動態行為利用雙軸模型來描述。
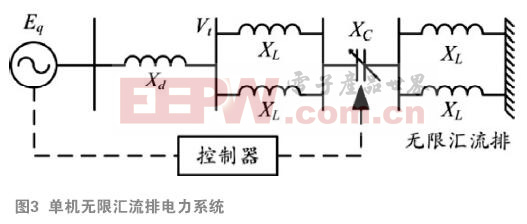
結合發電機、勵磁機方框圖,得到7個1階微分方程式,如式(3)至(9)。
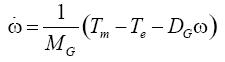 (3)
(3)
其中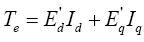 表示發電機經氣隙傳送的電磁功率。
表示發電機經氣隙傳送的電磁功率。
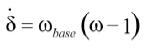 (4)
(4)
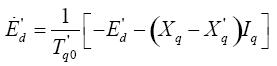 (5)
(5)
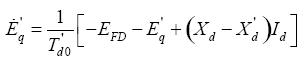 (6)
(6)
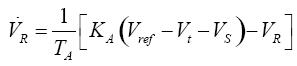 (7)
(7)
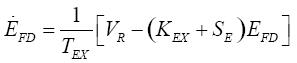 (8)
(8)
其中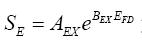 為勵磁機的飽和函數。
為勵磁機的飽和函數。
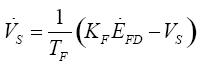 (9)
(9)
電網傳輸線與發電機端電壓關系式為:
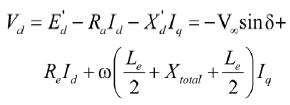 (10)
(10)
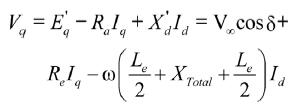 (11)
(11)
3 特征值分析
未加晶閘管控制串聯電容器前的開環系統,其完整的特征值列于表1的第2列,系統的機電振蕩模式不穩定。只加入晶閘管控制串聯電容器而未加入輔助控制器的完整特征值列于表1第3列,系統的低頻振蕩阻尼雖有改善,但仍不穩定。所以必須施加控制信號至晶閘管控制串聯電容器的控制機構。即![]() 為控制器輸出信號。
為控制器輸出信號。![]() 為使電力系統頻率誤差量有較好的動態響應,Ui根據系統輸出狀態量測量值的不同,而隨時發生變化。
為使電力系統頻率誤差量有較好的動態響應,Ui根據系統輸出狀態量測量值的不同,而隨時發生變化。

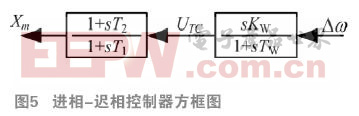
本文利用如圖5所示的進相-遲相控制器來增加低頻振蕩阻尼,控制器的傳遞函數如式(12),可以化成(13)至(14)兩個一階微分方程式。
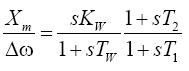 (12)
(12)
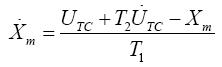 (13)
(13)
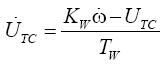 (14)
(14)
進相-遲相控制器的參數可以根據基于模態控制理論的極點指定法來決定。將不穩定的低頻振蕩模式特征值移至預設的穩定位置,經過簡單的矩陣運算,可得到控制器的參數值,詳細的運算法則如下所示。
對于一個控制系統,其狀態方程式可寫成: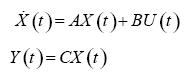
其中X(t)為n×1開環系統的狀態向量; U(t)為m×1系統的輸入向量,Y(t)為p×1系統的輸出向量,A、B、C均為常數矩陣。經過拉氏變換到頻域后,得:
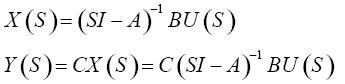
如果輸出至控制器的傳遞函數為U(S),m×p向量,則: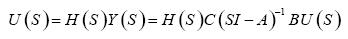
可得: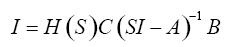
S代入指定特征值,經矩陣運算后,可得控制器U(S)中的參數。
極點指定法在使用時有以下幾點限制:
(1)所求得的控制器參數必須合理,且具可行性。如時間延遲常數需為正值,比例放大值不可過大等。
(2)必須使整個系統的特征值穩定。
(3)所指定的極點需合理,且不能影響整個系統其他部位的特性。根據以上法則,求得的結果如下:
預設特征值的低頻振蕩模式:-1.2±j6.0
進相-遲相控制器的參數為: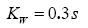 ,
,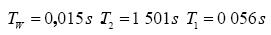 。
。
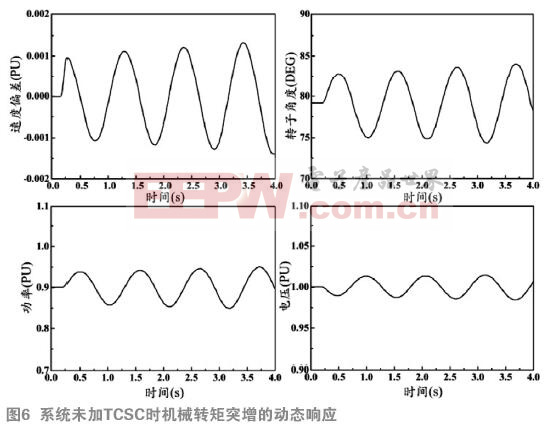
系統加入TCSC與進相-遲相輔助控制器后的特征值如表1第4列所示,機電模式振蕩的特征值準確的落在指定的位置上,其他模式的阻尼也得到了改善。
本文來源于中國科技期刊《電子產品世界》2016年第1期第54頁,歡迎您寫論文時引用,并注明出處。







評論