運算放大器電路中固有噪聲的分析與測量（第一部分）：引言與統計數據評論

　　我們可將噪聲定義為電子系統中任何不需要的信號。噪聲會導致音頻信號質量下降以及精確測量方面的錯誤。板級與系統級電子設計工程師希望能確定其設計方案在最差條件下的噪聲到底有多大，并找到降低噪聲的方法以及準確確認其設計方案可行性的測量技術。

　　噪聲包括固有噪聲及外部噪聲，這兩種基本類型的噪聲均會影響電子電路的性能。外部噪聲來自外部噪聲源，典型例子包括數字開關、60Hz 噪聲以及電源開關等。固有噪聲由電路元件本身生成，最常見的例子包括寬帶噪聲、熱噪聲以及閃爍噪聲等。本系列文章將介紹如何通過計算來預測電路的固有噪聲大小，如何采用 SPICE模擬技術，以及噪聲測量技術等。

熱噪聲

　　熱噪聲由導體中電子的不規則運動而產生。由于運動會隨溫度的升高而加劇，因此熱噪聲的幅度會隨溫度的上升而提高。我們可將熱噪聲視為組件（如電阻器）電壓的不規則變化。圖 1.1 顯示了標準示波器測得的一定時域中熱噪聲波形，我們從圖中還可看到，如果從統計學的角度來分析隨機信號的話，那么它可表現為高斯分布曲線。我們給出分布曲線的側面圖，從中可以看出它與時域信號之間的關系。

圖 1.1: 在時間域中顯示白噪聲以及統計學分析結果。

　　熱噪聲信號所包含的功率與溫度及帶寬直接成正比。請注意，我們可簡單應用功率方程式來表達電壓與電阻之間的關系 （見方程式1.1），根據該表達式，我們可以估算出電路均方根 (RMS) 噪聲的大小。此外，它還說明了在低噪聲電路中盡可能采用低電阻元件的重要性。

方程式 1.1：熱電壓

　　方程式 1.1 中有一點值得重視的是，根據該表達式我們還可計算出 RMS 噪聲電壓。在大多數情況下，工程師希望了解“最差條件下噪聲會有多嚴重？”換言之，他們非常關心峰峰值電壓的情況。如果我們要將 RMS 熱噪聲電壓轉化為峰峰值噪聲的話，那么必須記住的一點是：噪聲會表現為高斯分布曲線。這里有一些單憑經驗的方法即根據統計學上的關系，我們可將 RMS 熱噪聲電壓轉化為峰峰值噪聲。不過，在介紹有關方法前，我想先談談一些數學方面的基本原理。本文的重點在于介紹統計學方面的基本理論，隨后幾篇文章將討論實際模擬電路的測量與分析事宜。

概率密度函數：

　　構成正態分布函數的數學方程式稱作“概率密度函數”（見方程式 1.2）。根據一段時間內測得的噪聲電壓繪制出相應的柱狀圖，從該柱狀圖，我們可以大致看出函數所表達的形狀。圖 1.2 顯示了測得的噪聲柱狀圖，并給出了相應的概率密度函數。

方程式 1.2: 高斯曲線分布曲線對應的概率密度函數

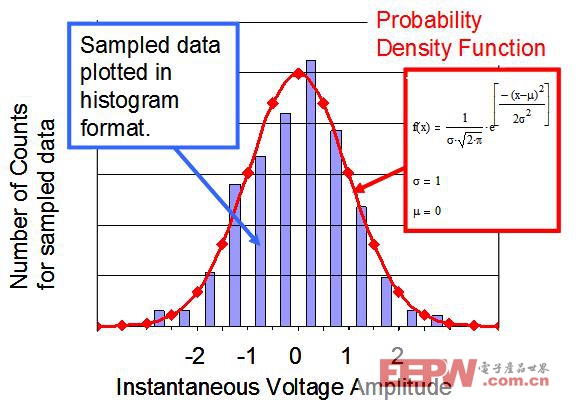圖1.2: 根據相應的概率密度函數所繪制的分布曲線。

概率分布函數：

　　概率分布函數是概率密度函數的積分。根據該函數，我們可了解某事件在給定的時間段內發生的概率（見方程式 1.3 與圖 1.3）。舉例來說，我們可以假定圖 1.4 為噪聲概率分布函數，該函數告訴我們，在任意時間點上，在 -1V 與 +1V 之間（即 (-1, 1) 區間內）檢測到噪聲電壓的概率為 30%。

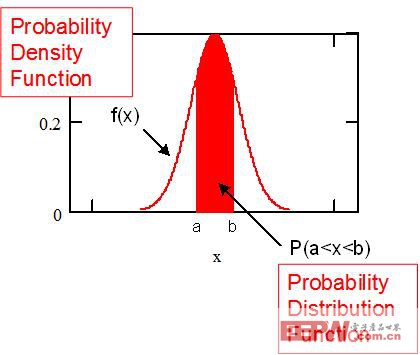圖 1.3: 概率密度函數與概率分布函數。

　　概率分布函數對我們將 RMS熱噪聲電壓轉化為峰峰值噪聲非常有用。請注意，高斯分布曲線的尾部是無限延伸的，這就是說，任何噪聲電壓都是可能的。盡管理論上確實如此，但就實際情況而言，極大的瞬時噪聲電壓發生的可能性不大。舉例來說，我們檢測到噪聲電壓在 -3σ 與 +3σ 之間的概率為 99.7 %。換言之，噪聲電壓超出該范圍的概率僅有0.3 %。因此，我們通常將噪聲信號的峰值估算為±3σ（即 6σ）。請注意，也有些工程師將噪聲的峰值估算為 6.6σ。人們對到底如何估計這個數值沒有定論。圖 1.4 顯示，68% 的噪聲都會不超過 2σ。表 1.1 總結了測量噪聲電壓時標準偏差與概率之間的關系。

圖 1.4: 標準偏差與峰值噪聲間的關系。

表 1.1: 標準偏差數與測量概率百分比

　　因此，在一定的標準偏差條件下，我們可以根據關系式來估算峰值對峰值噪聲。不過，總體來說，我們還是希望將 RMS 噪聲電壓轉化為峰峰值噪聲。人們常常假定 RMS 與標準偏差相同，不過事實并非總是如此。這兩個值只有在不存在 DC 元件（DC 元件為平均值 μ）的情況下才相同。就熱噪聲而言，由于沒有 DC 元件，因此標準偏差與 RMS 值相等。我們在附錄中舉出了“標準偏差與 RMS 相等”和“標準偏差與 RMS 不相等”兩個不同的示例。

　　文章開頭就給出了計算 RMS 熱噪聲電壓的方程式。還有一種計算 RMS 噪聲電壓的方法就是先測量大量離散點，然后采用統計學方法估算標準偏差。舉例來說，如果我們從模數 (A/D) 轉換器中獲得大量采樣，那么我們就能運用方程式 1.4, 1.5 及 1.6 來計算噪聲信號的平均偏差、標準偏差以及 RMS 值。附錄中的示例 1.3 顯示了在 Basic程序中如何運用上述方程式。我們在附錄中還列出了一組更全面的統計方程供您參考。

方程式 1.4、1.5、1.6：離散數據的統計方程

　　本文最后要介紹的概念是噪聲信號的疊加。為了疊加兩個噪聲信號，我們必須先了解信號是否相關。來自兩個不同信號源的噪聲信號彼此不相關。舉例來說，來自兩個不同電阻器或兩個不同運算放大器的噪聲是彼此不相關的。不過，噪聲源通過反饋機制會產生關聯。什么是相關噪聲源疊加呢？一個很好的實例就是帶噪聲消除功能的耳機，其可通過累加反向相關的噪聲來消除噪聲。方程式 1.7 顯示了如何疊加相關噪聲信號。請注意，就帶噪聲消除功能的耳機而言，相關系數 C 應等于 - 1。

方程式 1.7: 疊加隨機相關信號

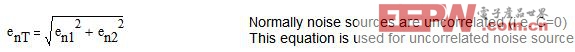方程式1.8: 疊加隨機不相關的信號

　　在大多數情況下，我們都要疊加不相關的噪聲源（見方程式 1.8）。在這種情況下疊加噪聲，我們要通過勾股定理得到兩個矢量噪聲的和。圖 1.5 顯示了疊加噪聲源的情況。我們通常可做近似地估計，如果一個噪聲源強度為另一個的三分之一，較小的噪聲源可忽略不計。

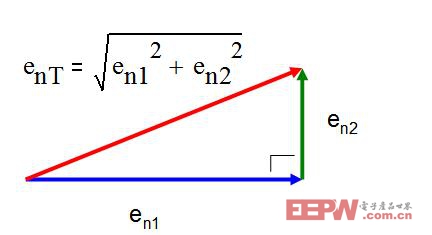圖 1.5: 噪聲勾股定理。

本文總結與后續文章介紹：

　　在關于噪聲的系列文章中，本文介紹了噪聲的概念，談論了噪聲分析所需的一些統計學基本原理。本系列文章中都將用到這些基礎知識。本系列文章的第二部分將介紹運算放大器的噪聲模型，并給出計算總輸出噪聲的一些方法。致謝：

特別感謝以下人員提供的技術信息：

德州儀器 (TI) Burr-Brown產品部
Rod Burt，高級模擬 IC 設計經理
Bruce Trump，線性產品經理
Tim Green，應用工程設計經理
Neil Albaugh，高級應用工程師

參考書目：

Robert V. Hogg與Elliot A Tanis共同編著的《概率與統計推斷》，第三版，麥克米蘭出版公司 (Macmillan Publishing Co)出版；

C. D. Motchenbacher與 J. A. Connelly共同編著的《低噪聲電子系統設計》，A Wiley-Interscience Publication出版。

關于作者：

　　Arthur Kay 現任 TI 的高級應用工程師。他專門負責傳感器信號調節器件的支持工作。他于 1993 年畢業于佐治亞理工學院 (Georgia Institute of Technology) 并獲得電子工程碩士學位。他曾在 Burr-Brown 與 Northrop Grumman 公司擔任過半導體測試工程師。

附錄 1.1:
例 1: 本例中，RMS 值與標準偏差不等。通常說來，如果存在 DC 元件的話，標準偏差與 RMS 值不等（即非零平均值）。

附錄 1.2:
例2：本例中，RMS 等于標準偏差。通常說來，如果不存在 DC 元件的話，標準偏差與 RMS 相等（即零平均值）。

附錄 1.3:
例 3：計算平均偏差、標準偏差及 RMS 值所采用的 Basic 程序

附錄 1.4:
采用概率分布函數的統計方程

附錄1.5:
采用適用于測量數據的統計方程

作者：德州儀器公司高級應用工程師，Art Kay