一種基于BP神經網絡的手勢識別系統設計

　　0 引 言

　　隨著科技的發展和進步，計算機已經漸漸適應人的需求。人類在利用計算機解決問題時，并沒有將主觀能動性和計算機的高效性有機地結合起來。研究新型的人機交互工具能夠打破這一障礙。當虛擬現實越來越被人熟知時，可以使用手勢作為載體進行人機交互。

　　目前，手勢輸入的種類有基于圖像的和基于加速度傳感器的。由于圖像的手勢識別對外部環境的依賴比較大，而加速度傳感器識別就不受外部條件的限制，甚至可以依靠單手完成操作，因此，基于加速度傳感器的方法能有效地識別手勢動作，完成人機交互。本文采用ADXL335 三軸加速度傳感器分別采集五個手指和手背上的加速度信息，實現手勢的輸入。

　　1 手勢識別方法

　　手勢的執行是一個動態的過程，主要表現在手指彎曲引起的手的形狀和手在空間的位置和方位的變化，需要從時間和空間兩方面來描述。根據手勢的時變特征，可將手勢分為靜態手勢和動態手勢。從測量的角度看，靜態手勢可用某一時刻手的空間特征的測量值來表示，而動態手勢是指需要使用隨時間變化的空間特征來描述的手勢。靜態手勢可以用各個關節測得的特征值來表示，而動態手勢需用一段時間內手的空間特征的一組測量序列值來表示。人的手有多個自由度，運動十分靈活、復雜，而且不同的人，手的大小不同。因此，同樣的手勢，不同的人作出時手的運動會存在差別;同一個人在不同的時間、地點作出手勢也不一樣。所以，本文主要針對靜態手勢的數據手套進行分析研究。

　　2 手勢的識別技術

　　目前，比較流行的手勢識別技術有模板匹配法、特征提取和BP 算法等。

　　模板匹配法：主要是將傳感器輸入的原始數據與預先存儲的模板進行匹配，通過測量兩者之間的相似度來完成識別任務。由于需要大量的基礎數據作為匹配對象，所以受到噪聲、光照、復雜環境影響較大，并且匹配速度慢。但是，模板匹配法簡單、易掌握，普及程度高。

　　特征提取：在特征提取過程中，輸入數據中的低層特征被提取出來，經過分析而轉化成包含手形語義的高層特征，然后用高層特征進行手形識別。

　　BP 算法：是一種按誤差逆傳播算法訓練的多層前饋網絡。

　　BP 網絡的學習規則是使用最速下降法，通過反向傳播來不斷調整網絡的權值和閾值，使網絡的誤差平方和最小。

　　3 BP 算法

　　BP 神經網絡是一種前向傳播的多層網絡，網絡除了輸入節點以外，還有一層或多層隱含節點。其訓練方法被稱為誤差反傳播算法，它利用實際輸出和期望輸出之差對網絡的多層連接權由后向前逐層進行校正。BP 網絡的最大缺點是樣本訓練的收斂速度慢。為提高網絡的收斂速度，同時防止網絡的振蕩發散，本次選取的BP 神經網絡是1 個3 層BP 網絡結構( 含1 個隱層)，隱單元及輸出單元用sigmoid 函數輸出，輸出共分為10 類，即輸出神經元個數為10.由于輸入矢量為處理后的手部加速度傳感器( 用18×10 的數字矩陣表示) ，因此第一層為240 個神經元，第二層為隱含層。根據經驗，其神經元數目一般為輸入矢量維數的10 %，為26 個神經元，采用改進的BP 算法。將每個樣本對應的矩陣元素值輸入神經網絡的各個輸入單元，并為每個輸出單元指定期望輸出，計算每個輸出單元的實際輸出與期望輸出的誤差以及隱含層誤差。計算實際輸出與期望輸出的誤差公式為：

　　式中的負號表示梯度下降，常數η ∈(0，1)代表學習速率。

　　由于BP 神經網絡算法的收斂速度慢，優化的目標函數非常復雜，所以需要優化學習速率。三層感知器的BP 學習算法權值調整計算公式為：

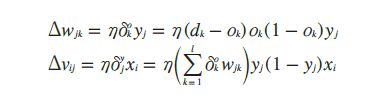
　　將每個加速度傳感器中每個軸的數據特征向量作為神經網絡的輸入，所以神經的輸入層神經元個數等于特征向量的維數，即9×18=162 個輸入神經元。輸出層神經元個數的確定因為要識別10 個數字，因此輸出選擇為10×1 的矩陣，即輸出節點數為l0.當0 ~ 9 輸入神經網絡后在輸出神經元對應的位置上為1，其他的位置為0.輸入數字0，第1 個輸出神經元為1，其他為0 ;輸入數字1，第2 個輸出神經元為1，其他為0 ;依此類推。

　　隱含層數越多， 神經網絡學習速度就越慢。根據Kosmogorov 定理，在合理的結構和恰當的權值條件下，3 層BP 網絡可以逼近任意的連續函數。因此，我們選取結構相對簡單的3 層BP 網絡。

　　一般情況下，神經元個數與函數收斂程度有關。根據經驗公式s=sqrt(n×m)，其中，m 為輸入神經元個數，n 為輸出神經元個數，得出隱含層神經元個數為40 個。

　　采用定義學習速率和采用帶動量因子算法兩種改進方法。

　　識別內容為數字0 ~ 9，利用手勢特征，提取每個加速度傳感器中每個軸的數據作為BP 的數據輸入參數，為BP 進行初始化及參數訓練，可以提高數據的識別率。在學習收斂的情況下，增大η，以縮短學習時間;當η 偏大致使不能收斂時，要及時減小η，直到收斂為止。將上一次權值調整量的一部分迭加到按本次誤差計算所得的權值調整量上，作為本次的實際權值調整量，即：

　　4 實驗結果分析

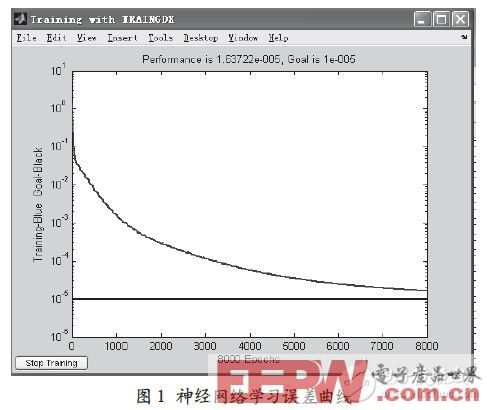
　　通過Matlab 計算所得出得神經網絡學習誤差曲線和數字識別結果如圖1 所示。

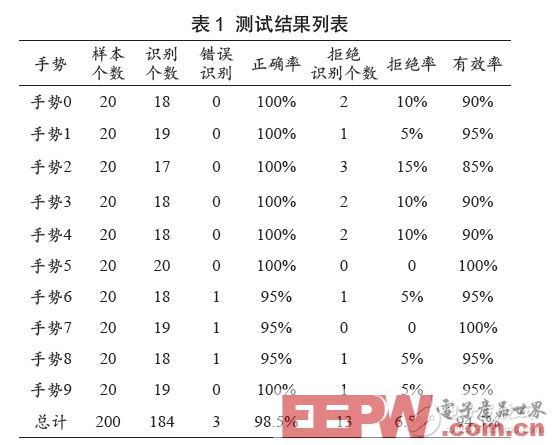
　　本文將0 ~ 9 共10 類數據中的每類取20 個做測試樣本，共200 個測試樣本對系統進行性能測試。測試結果如表1 所列。由表1 中的數據可知，數字識別的正確率為98.5%，正確率較高，拒識率為6.5%，也比較高。總體數字識別有效率為94.5%.Kadous 用Power Gloves 作為手語輸入設備，這樣的識別率僅為80%.

　　5 結 語

　　實際上，數字識別的正確率和拒識率與數字識別的判斷值有關，本文的判斷值設置為0.7.判斷值設置得高，數字識別的正確率就高，同時數字的拒識率也相應地就高，反之亦然。因此，判斷值的選擇需要根據實際情況來定。