飛行體姿態角的測試方法

　　飛行體姿態角的測試方法有很多種，如磁敏傳感器、高速攝影儀、加速度計法以及陀螺儀等。各種方法都有其優點及應用局限，適用于不同的應用場合。某小型飛行體飛行過程中所受過載較小，姿態角變化不大，可容納測試儀的空間有限，針對該小型飛行器姿態角測試，提出了一種基于陀螺儀的姿態角存儲測試方法，介紹了具體實現方案。

　　2 姿態角測試系統設計

　　磁敏傳感器法通常只是作為一種輔助測試手段，高速攝影法易受天氣影響也限制了它的應用。加速度計法有著低成本、低功耗、高可靠性等優點，但是理論計算及安裝復雜限制了該方法的應用，在國內多以理論研究為主。而陀螺儀法在過載不太大的場合應用方便，成為此飛行器姿態角測試的一個很好的選擇。飛行體的姿態運動是飛行體繞自身質心的轉動運動。在引入剛體假設和坐標系轉換的概念后，飛行體的姿態定義為飛行體坐標系相對于參考坐標系的旋轉變換。

　　2．1 陀螺儀姿態角測試原理

　　在對剛體的轉動運動進行解析描述時．常應用歐拉角或卡爾丹角。卡爾丹角適用于姿態角變化較小的場合，因此．用卡爾丹角進行描述。取初始時刻飛行體坐標系Oξηζ為固定坐標系，0xyz為與飛行體固結的動坐標系。卡爾丹角選取的方法是，首先繞ξ軸轉過α角，到達0x1y1zl的位置；再繞y1軸轉動β角，到達0x2y2z2的位置；再繞z2軸轉動γ角，到達0xyz的位置。轉動關系如圖l所示。

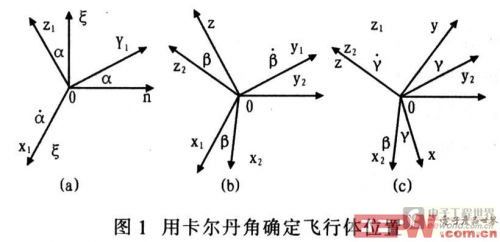
　 α、β以及γ分別為沿0ξ軸、0y1軸與0z軸的角速度分量，三次轉動如式（1）所示：

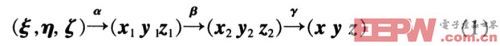
　　在此，以cx表示cosx、sx表示sinx，正切以tgx表示。各次轉動相應的方向余弦矩陣分別為

　　飛行體的角速度ω，可以表示為：

　　式(7)為卡爾丹角表示的運動學微分方程，其中ωx、ωy及ωz分別為陀螺x軸、y軸及z軸的輸出。積分此式，可得卡爾丹角。

　　2．2 系統實現

　　研究存儲測試技術之后，設計了存儲測試系統。體積微小和測量時不需要引線即不需要對外界的電磁輻射是他的最突出特點。在動態參數的存儲測試領域，測試儀要隨被測體一起運動，要求測試系統具有體積小、功耗低及抗高過載等特點，下面將結合系統設計闡述這些要求的相應解決措施。

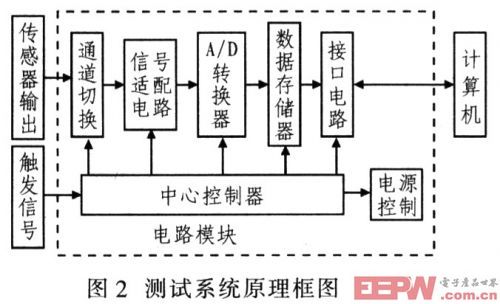
　　主控器件能否正常工作，是整個系統能否可靠獲得被測參數的關鍵。CPLD輸入和輸出引腳的原始電平可預先設定，開機即能達到預定電平，狀態明確。信號傳輸效率高，適合高速采樣場合。可編程邏輯宏單元或邏輯塊之間的相互連線在同一封裝內，受外界干擾影響小，電磁兼容(EMC)性能好。綜上所述，CPLD具有邏輯性強、響應時間快、程序不易跑飛等特點。為此選用CPLD作為主控器件，設計盡量簡單可靠的器件內部邏輯，以確保整個測試過程系統的正常工作。本系統存儲容量為512 Kxl2 bit，負延遲為128 Kxl2 bit，采樣頻率為8 kHz。測試系統原理框圖如圖2所示。