完美的時序:用抖動與相位噪聲測量做時鐘分頻
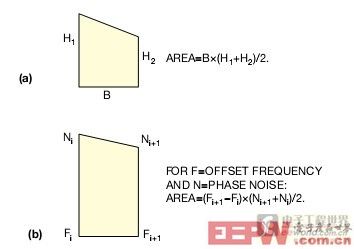
圖7,將所有梯形面積求和,就獲得了曲線下的面積。將結果乘以2,就確定了最終的rms抖動值。
圖7中一塊梯形面積的方程用于尋找兩個相鄰數據點對所描述的區域。將所有這些梯形面積加起來,就找到了曲線下的面積。最終的rms抖動值由兩個因數對結果的縮放而決定:值的來源是,數據取自一個單邊帶;然而,rms抖動被假設為雙邊帶的。假設相位噪聲的兩個邊帶對時鐘頻率為對稱,通常是安全的。這種情況下,由于一個限幅放大器抑制了AM(幅度調制),而通過FM(頻率調制),確保了對稱的邊帶,因此就更加安全(圖8)。
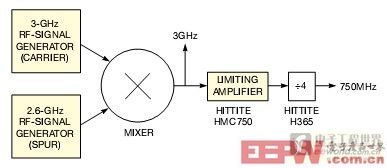
圖8,限幅放大器抑制AM,而讓FM通過,確保了對稱的邊帶。
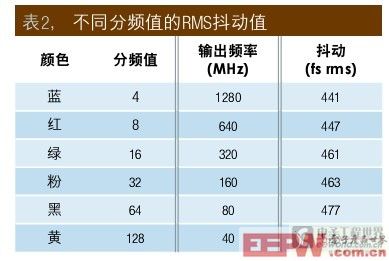
表2, 不同分頻值的RMS抖動值
另外一個縮放因素用于轉換總面積,使之不再用UI(單位間隔),而是用時間單位。這個因數在相位噪聲值變化時,將rms邊沿抖動值保持為相對恒定。rms抖動的方程如下:
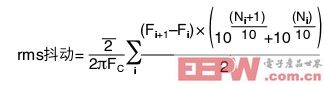
其中,FC?是時鐘頻率,Ni?是第i項對每赫茲載波的相位噪聲(分貝),而Fi?是第i項的偏移頻率。
混疊
混疊是時鐘頻率降低時,rms抖動值增加的另一個原因。相位噪聲圖的上半部分向下混疊到新的較低頻相位圖上。由于相位噪聲通常略高于時鐘或載波頻率,并隨與時鐘頻率的偏移增加而減小,因此只有少量相位噪聲被混疊。但是,當被大數除時,這個效應就會累積,變得明顯。例如,圖1中1280與640MHz曲線之間的差在整個圖上都是恒定的6dB。于是,你會預期,表2中的兩個曲線增加的rms抖動值應整體混疊,而不是儀器的本底噪聲。
圖9至圖13中的頻譜與相位噪聲圖顯示了混疊情況。這些例子中的信號都使用AM來演示混疊,而在一個典型應用中它們是不希望出現的。圖9與圖10表示的是3GHz信號的頻譜與相位噪聲圖。圖中顯示了在3GHz時鐘頻率上下400MHz頻率的對稱尖刺。當頻譜顯示兩個相等的邊帶時,同一信號的相位噪聲圖包括了它們從一個3GHz載波進入一個毛刺400MHz的效應。然后,一個四分電路對3GHz信號做分頻,產生750MHz。
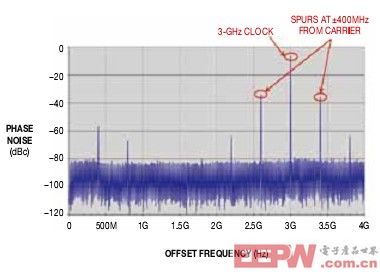
圖9,對稱毛刺以400 MHz頻率出現在3 GHz時鐘頻率的上下方。
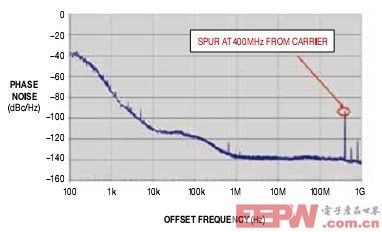
圖10,當頻譜顯示兩個相等邊帶時,相同信號的相位噪聲圖將其效應結合到3 GHz載波的一個400 MHz尖刺內。然后一個四分電路將3 GHz信號分頻,生成750 MHz。



評論