基于Matlab和Visual C++的數字濾波器設計方法

4 時域傳遞函數

Matlab一般只用于功能仿真，而實際項目應用，通常采用Visual C++軟件編程進行信號控制和硬件實現，所以需要將Matlab仿真時使用的濾波器函數Filter轉化為C代碼實現。

軟件編程有時域和頻域兩種思路。由于輸入信號較為復雜不易進行時-頻轉換，只能采用時域濾波。所以需將傳遞函數反變換到時域，對信號進行濾波處理。

5 時域卷積濾波

卷積在通信技術和信號處理中起著重要的作用。在線性時域系統中，根據時間的連續性，可以分為卷積積分和卷積和。在LTI連續時間系統中，把激勵信號分解為一系列沖激函數，求出各種沖激函數單獨作用于系統時的沖激響應，然后將這些響應相加就得到系統對于該激勵信號的零狀態響應。這個相加的過程表現為求卷積積分。在LTI離散系統中，可用上述方法進行分析。由于離散信號本身是一個序列，因此，激勵信號分解為單位序列的工作就較容易完成。如果系統的單位序列響應為已知，那么，也不難求得每個單位序列單獨作用于系統的響應。把這些序列相加就得到系統對于該激勵信號的零狀態響應，這個相加的過程表現為求卷積和。

由于本系統中的信號是離散時間序列，常用的卷積和的求解方法有圖解法、對位相乘求和法、解析法和列表法等4種。一般，待處理的信號的數據量比較大，列表法不適用，所以采用解析法。

卷積與傅里葉變換有著密切的關系。利用兩個函數的傅里葉變換的乘積等于它們卷積后的傅里葉變換的性質，能使傅里葉分析中許多問題的處理得到簡化。本文正是采用這一點，將頻域的濾波轉化為時域濾波。

頻域相乘等效于時域卷積。編寫C程序求輸入信號和傳遞函數的卷積和。當兩個信號為因果信號時，可以根據式(5)求卷積和。當f1(k)的數據長度為m;f2(k)的數據長度為n(n

6 結果及分析

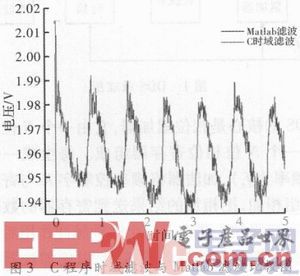
信號分別經卷積和濾波和Filter函數濾波，將濾波后的數據導入Matlab比較，結果如圖3所示。由圖可見，前者在初始狀態出現尖峰，這是因為卷積和是在特定窗口內時域累加的過程，會造成頭部數據和尾部數據不準確。雖然編寫的C卷積和濾波程序有一定的缺陷，但是整體波形一致，說明實驗獲得初步成功。

7 結束語

提出了一種將硬件濾波電路數字化的方法，并在Matlab和Visual C++平臺上得以實現。與模擬濾波電路和傳統的數字濾波相比，不僅比傳統的數字濾波算法簡單快捷，而且有效防止了模擬電路中器件的寄生參數、精度、溫度等的影響，使濾波更加穩定。