耦合濾波電感原理

應幾位網友的要求，下面給大家簡單講講在buck變換器基礎上發展出來的正激、半橋、推挽和全橋PWM變換器多路輸出中常采用的耦合濾波電感的工作原理。因為水平有限，只能用仿真軟件來簡單介紹一下工作原理和設計思路。

常見的PWM控制的正激、半橋、推挽和全橋，其實質還是一個buck變換器。為了簡化分析過程，變壓器前面的部分我就不說了。僅僅從變壓器后面部分開始說明。

對于多路輸出的電源，通常變壓器次級有多個繞組，按照不同的輸出電壓要求，繞組的匝數按照相應的比例來設計。但是反饋回路一般只有一個，而且通常是取功率輸出最大的那一路來反饋。

假設有這么一個正激電源，輸出為：

5V/10A

3.3V/20A

實際電源中，反饋回路是從3.3V這路取樣。

再假設每路輸出的整流管都是二極管，壓降為0.5V。

再假設如下參數：

開關頻率f=50KHz

滿載占空比，低壓輸入時為Dmax=0.4

高壓輸入時為Dmin=0.2

那么根據這些參數，我們可以來計算每一路的濾波電感的數值應該為多少，假設電流的紋波為20%，根據工作原理，最大電流紋波出現在最高輸入電壓最大輸出負載時：

由此我們也可以知道變壓器次級5V繞組和3.3V繞組之間的匝比關系為：

n=13.75/9.5=1.447

有了以上參數，我們就可以建立一個簡單的電路模型來模擬雙路輸出的正激變換器的次級部分了。為了簡單起見，我們采用開環控制，這樣的話，輸出一開始會有過沖，我們可以等穩定以后再分析數據，忽略前面過沖的部分。實際電路由于有反饋環，過沖是不存在的。我們用Vpulse這么模型來模擬次級的變壓器繞組輸出，二極管采用MBR2540，電感和電容都是采用的理想元件，沒有考慮ESR等雜散參數。建立如下電路圖，模擬在最低輸入電壓兩路都是最大輸出時的狀態：

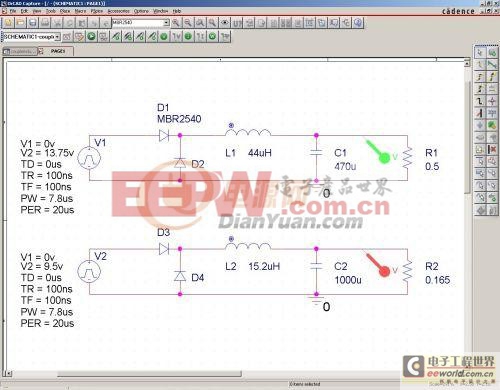
然后如下參數設定時域掃描

掃描完成后，觀察輸出電壓：

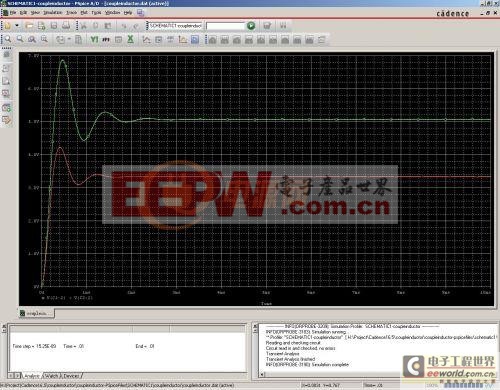
從圖上可以看出，待穩定后，輸出電壓是正常的，滿足設計要求。

看看此時兩個電感的電流波形，注意要把電壓探頭刪掉，換成兩個電流探頭，分別放在兩個電感輸入端，同時把波形圖的橫坐標展開，觀察9.9ms到10ms這部分：

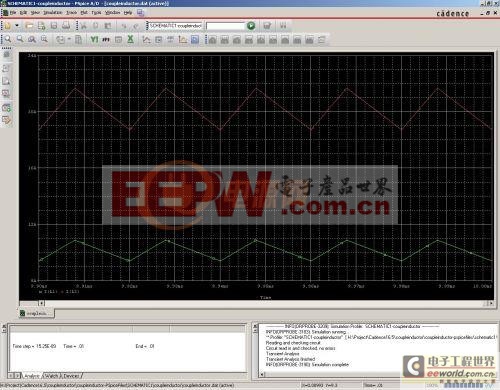
從電感電流波形可以看出，兩路輸出的電感電流都是處于連續模式的。

現在假設，3.3V輸出的負載不變，5V輸出的這路輸出電流降低，輸出電流從10A降到了0.25A，因為實際電源的反饋是取自3.3V輸出的。那么由于3.3V這路的輸出沒有改變。所以電路的工作占空比沒有發生變化，那么這時候，會發生什么事情呢？

首先修改5V的輸出負載電阻為20歐。

然后，修改時域掃描的時間，把掃描時間增加為20ms，以保證輸出完全穩定下來，仿真結束后，如上圖再次放上電壓探頭，看看此時的輸出電壓是如何變化的：

從圖中可以看出，3.3V那路的輸出還是正常的，而5V那路的輸出已經飆升到了7.5V左右。

同樣把電壓探頭刪掉，換成電流探頭，看看電感電流波形。只不過，這次把時間軸設置成19.9ms～20ms，看看：

從圖中可以看出，5V輸出這路，由于負載電流太小，已經進入了DCM模式。那么輸出電壓已經不再是Vout=Vin×D了。

這就是多路輸出，獨立濾波電感存在的一個嚴重問題。為了解決這個問題，就引入了耦合電感這個方法。

在實際設計過程中，通常把所有的輸出都折算到某一路輸出來計算磁芯的參數，然后按照每路輸出電流來選擇線徑。同時，必須使每路輸出電感的匝數比與變壓器次級每個繞組的匝數比相同！

我們來嘗試計算一下：

假如把5V繞組輸出折算到3.3V繞組的輸出，那么：

Iout=（5×10+3.3×20）/3.3=35.15A

輸出濾波電感應該為

有了這兩個數值，我們就可以根據AP法求出實際的磁芯大小。這里我就省略了。

我們前面已經有了5V變壓器繞組和3.3V變壓器繞組的匝比關系n=1.447，現在根據能量的關系來計算耦合電感的每一路輸出的電感量：

把原理圖中的兩個電感的電感量分別設置為以上參數。然后放置一個耦合元件K_Linear，并將其參數L1、L2分別設置為兩個電感的名字l1，l2。設置好負載電阻的阻值：

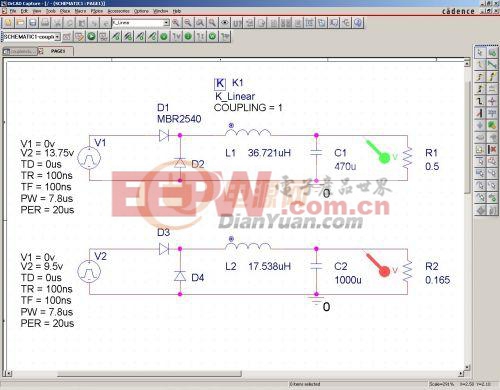
先看看都是滿載輸出的時候的情況，輸出電壓：

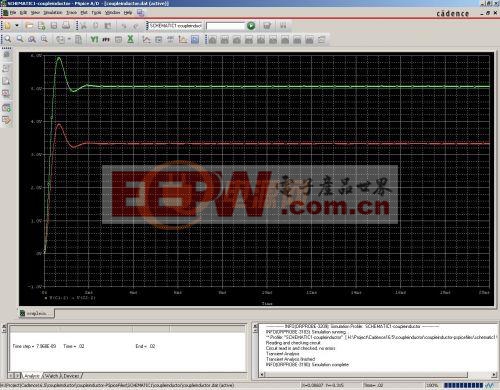
從圖中可以看出，輸出電壓都是正常的，滿足設計需要。再看看把5V輸出的負載電阻改成20歐的結果會怎么樣，下面是仿真后的輸出電壓波形：

可以看到，即便把5V的輸出負載變成20歐，此路輸出的電壓依然能夠保持在一個比較正常的值，而不像獨立電感時，電壓會飆升到7.5V。這就是耦合電感帶來的好處。

很慚愧，我并沒有耦合電感輸出的正激電源的設計經驗。所以，以上只能從基本原理的角度給大家一些原理性分析。具體的設計過程是否合理，我不能確認。歡迎有此類設計經驗的朋友參與討論。另外，實際的工程設計中，元件不是理想化的，耦合電感會存在漏感，而漏感也會影響交叉調整率，所以，實際情況會復雜的多，耦合電感的結構設計會非常重要。