為什么功率最大意味著靈敏度最低?
對(duì)于各種濾波器設(shè)計(jì)和網(wǎng)路理論問(wèn)題進(jìn)行深入探討是值得關(guān)注的話題。本文在此討論的主題為採(cǎi)用雙端接LC梯型濾波器的拓樸結(jié)構(gòu)。首先,我必須將來(lái)源電阻和負(fù)載電阻設(shè)置為相同的值。由于電感器和電容器構(gòu)成的網(wǎng)路具有兩個(gè)‘埠’,以供訊號(hào)進(jìn)入和離開(kāi)網(wǎng)路。在我們的濾波器中,輸入埠從具有特定電阻值的來(lái)源處獲得訊號(hào)(一般無(wú)法變更),輸出埠則連接到由另一個(gè)電阻構(gòu)成的‘負(fù)載’(通常可以加以控制)。
圖1顯示的是範(fàn)例濾波器。其輸出端設(shè)計(jì)採(cǎi)用與來(lái)源電阻值一樣的電阻端接。圖2顯示的是非常良好且平坦的通帶響應(yīng)。圖3顯示在移除端接電阻后的較差響應(yīng)。
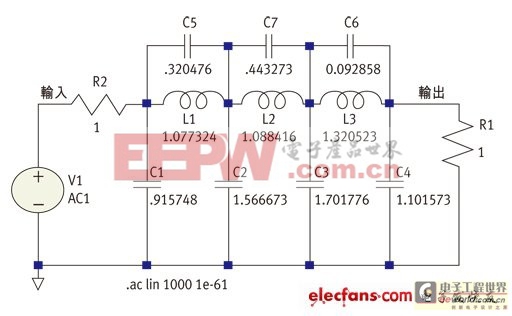
圖1: 雙端接低導(dǎo)通濾波器網(wǎng)路範(fàn)例。
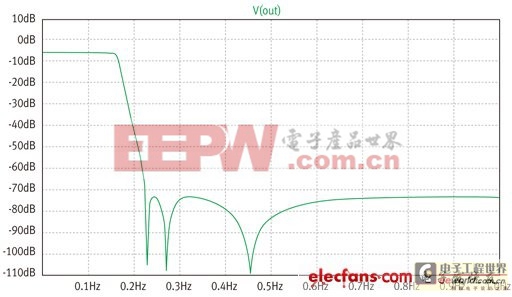
圖2:圖1元件在具有負(fù)載電阻時(shí)的電壓增益。
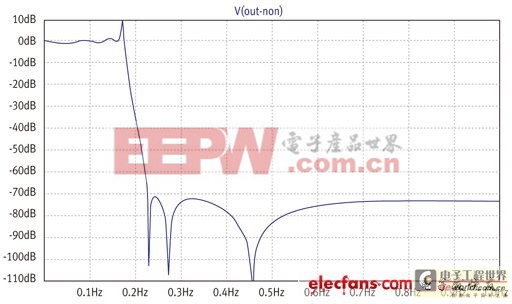
圖3:圖1元件在無(wú)負(fù)載電阻值時(shí)的電壓增益。
我們可以看到,對(duì)于本文所用的特定元件值,低漣波平坦響應(yīng)只有在加入負(fù)載電阻的情況下才會(huì)出現(xiàn)。但這并非是具有兩個(gè)電阻的結(jié)果。圖4是在無(wú)負(fù)載電阻情況下產(chǎn)生同等振幅響應(yīng)(圖5)的網(wǎng)路值集合。其電壓增益為0dB,而非6dB。但你是否真的會(huì)在大多數(shù)實(shí)際情況中使用該濾波器?答案不言而喻,因?yàn)轫憫?yīng)相同,而增益更大,而且可以節(jié)省一個(gè)元件,誰(shuí)不喜歡呢?

圖4:無(wú)負(fù)載電阻的各種元件值組合。
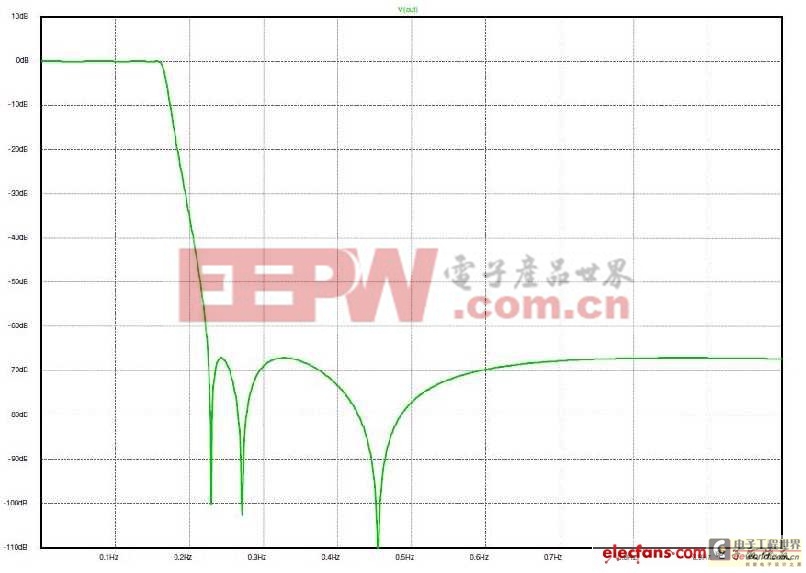
圖5:無(wú)負(fù)載電阻時(shí),響應(yīng)依舊非常出色且平坦。
圖6和圖7說(shuō)明了我們抗拒採(cǎi)用‘單端接’誘惑的塬因。這兩張圖是元件值在±5%允許範(fàn)圍內(nèi)變化時(shí),100個(gè)響應(yīng)曲線疊加在一起的狀況。我們可以清晰地看出雙端接濾波器更能夠適應(yīng)所使用元件值的小幅度變化。在下文中還可以看到當(dāng)我們使用某些擴(kuò)展技巧時(shí)──在不使用這些電感器的情況下,以這些網(wǎng)路為‘塬型’構(gòu)建主動(dòng)濾波器──這種特性仍然得以保留。
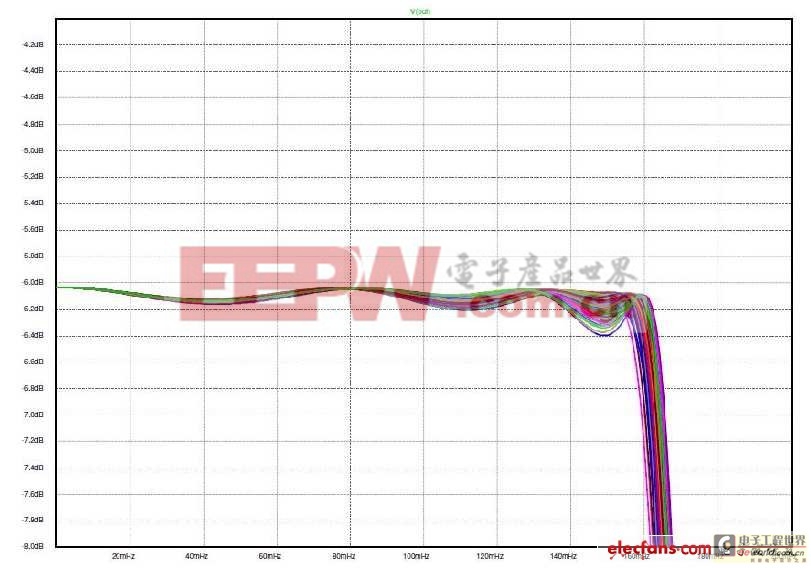
圖6:對(duì)圖1值的蒙特卡羅分析。
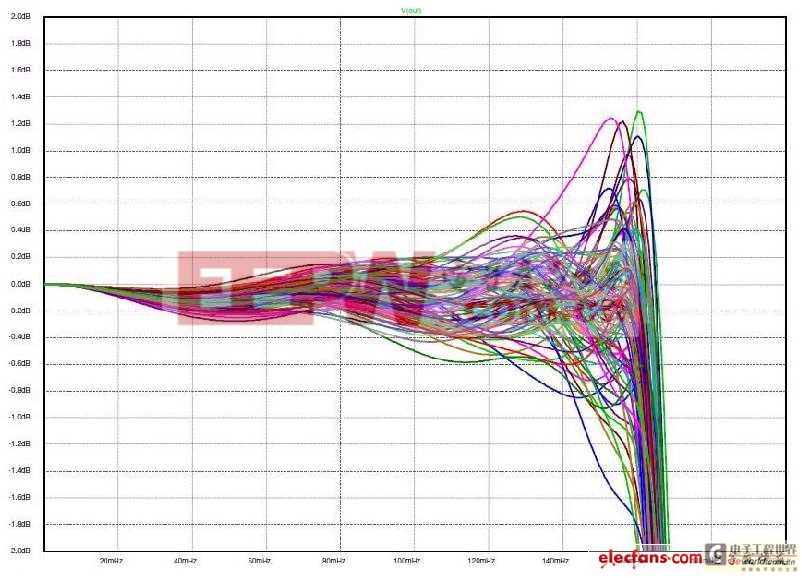
圖7:對(duì)圖4值的蒙特卡羅分析。
雙端接濾波器有什么特別之處呢?要回答這個(gè)問(wèn)題,我們必須考慮當(dāng)訊號(hào)從來(lái)源電阻通過(guò)LC網(wǎng)路到負(fù)載電阻時(shí)時(shí),到底發(fā)生了什么?
稍微岔開(kāi)一下話題。想像一下你正在面試一個(gè)類(lèi)比設(shè)計(jì)職務(wù),并要求回答下面的問(wèn)題:
“你有一個(gè)50歐姆輸出阻抗的正弦波產(chǎn)生器,開(kāi)路的情況下可以輸出1Vrms的電壓。客戶給你一個(gè)輸入阻抗為3.3K歐姆的黑盒子;如果該黑盒子要能正常工作,需要至少3Vrms的50KHz輸入訊號(hào)。你必須讓系統(tǒng)工作,但卻沒(méi)有電源。你在實(shí)驗(yàn)室唯一能夠使用的電子元件是雙導(dǎo)線的被動(dòng)元組件。請(qǐng)說(shuō)明如何解決上述問(wèn)題及其工作塬理。”(案例1)
那么這個(gè)挑戰(zhàn)就在于沒(méi)有電池或太陽(yáng)能電池,也沒(méi)有電晶體或整合電路,而且肯定也沒(méi)有變壓器。在繼續(xù)讀下去之前(特別是你準(zhǔn)備參加面試的情況下)請(qǐng)先好好想想。也許我們可以從圖2找到一些靈感。想到了嗎?這裡有個(gè)適用的解決方案:
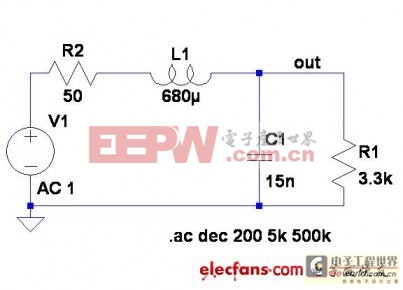
圖8:適合案例1的解決方案。
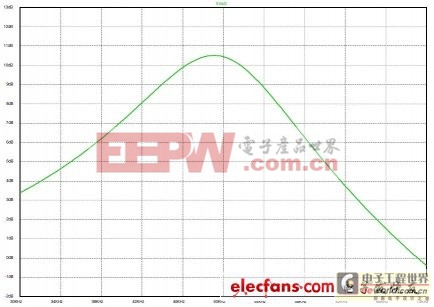
圖9:圖8解決方案的頻率響應(yīng)
我們只使用被動(dòng)雙導(dǎo)線元件構(gòu)建一個(gè)高Q值的低導(dǎo)通濾波器。圖9顯示的是訊號(hào)產(chǎn)生器上設(shè)置為1Vrms開(kāi)路輸出到黑盒子電壓的全頻段狀況。我們明確地實(shí)現(xiàn)了讓系統(tǒng)在規(guī)定頻率上工作的電壓增益。那么,哪兒可找得到免費(fèi)的午餐呢?
當(dāng)然什么地方都不會(huì)有。但我們可以問(wèn)個(gè)問(wèn)題:“我們能夠從這類(lèi)解決方案中得到的最大電壓增益值是多少?”要得到結(jié)果,首先要認(rèn)識(shí)到,雖然從這樣的元件組合中得到電壓增益是常見(jiàn)的,但不可能得到功率增益。這就是理解這些被動(dòng)濾波器網(wǎng)路的關(guān)鍵所在:功率進(jìn)入網(wǎng)路,然后離開(kāi)網(wǎng)路。如果來(lái)源能在特定輸出電阻上提供特定的輸出電壓,對(duì)于連接的負(fù)載而言,能夠耗散的功率有嚴(yán)格的上限。你可能在學(xué)校中學(xué)習(xí)過(guò)最高功率塬理(Maximum Power Theorem),但卻未曾多加注意。但對(duì)被動(dòng)濾波器而言,這個(gè)塬理非常重要,今后請(qǐng)予以相當(dāng)?shù)年P(guān)注。
你可能已經(jīng)想起來(lái)了,實(shí)現(xiàn)最高功率傳輸?shù)臈l件是負(fù)載電阻和來(lái)源電阻相等。你可以使用大學(xué)?媥ガ鴘漪燥無(wú)味的微積分來(lái)證明。先用一個(gè)敘述來(lái)表達(dá)負(fù)載電阻上耗散的功率,根據(jù)負(fù)載電阻RL計(jì)算該功率的導(dǎo)數(shù)。將導(dǎo)數(shù)設(shè)為0,然后求解RL。
是不是一下子就豁然開(kāi)朗了?你首先想到的是用變壓器。這是讓負(fù)載電阻與來(lái)源電阻匹配的傳統(tǒng)方法。在理想的情況下,變壓器可以把功率從來(lái)源無(wú)損地傳輸?shù)截?fù)載,不過(guò)它一般用于電壓、電流不同的情況下。使用適當(dāng)?shù)脑褦?shù)比(turns ratio),不論負(fù)載電阻值是多少,都可以在理想的情況下在負(fù)載電阻上獲得相同的耗散功率。
這就是我們對(duì)圖8的LC濾波器網(wǎng)路採(cǎi)用的措施:我們導(dǎo)入了一個(gè)變壓器。所有進(jìn)入LC網(wǎng)路的功率又出去了。在採(cǎi)用正確元件值的情況下,我們可讓所有功率在特定頻率上全部到達(dá)負(fù)載上,而無(wú)論負(fù)載的值是多少。
如果我們可以使用變壓器或者變壓器的等效LC線路,我們可以計(jì)算出50歐姆來(lái)源和3.3K歐姆負(fù)載之間能夠獲得的最大電壓增益。所需的電壓轉(zhuǎn)換等于阻抗比的平方根,在本例中為8.12倍。將該比例與我們?cè)诘刃щ娮瓒私永又械碾妷涸鲆?.5相乘。所以在任意LC值下可以得到的最大增益為4.06倍,或者大約12.2dB。圖10顯示以我們自製的變壓器任意選擇1,000種不同的L和C值得到的結(jié)果。響應(yīng)曲線的峰值從未超過(guò)預(yù)計(jì)值。至于為什么不是每個(gè)頻率下所有功率都耗散在負(fù)載上?那是因?yàn)椴糠莨β时环瓷浠貋?lái)源。
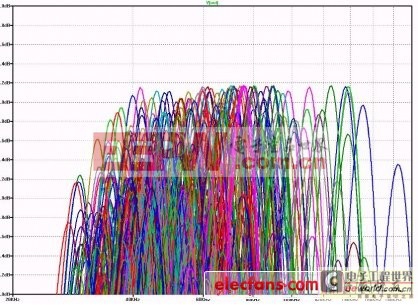
圖10:響應(yīng)曲線的峰值從未超過(guò)預(yù)計(jì)值。
所有射頻工程師都開(kāi)始不耐煩地打哈欠了,因?yàn)檫@對(duì)你們來(lái)說(shuō)相當(dāng)稀鬆平常。設(shè)計(jì)LC網(wǎng)路,確保讓所有來(lái)源的功率傳輸?shù)截?fù)載,是一項(xiàng)稱之為阻抗匹配的核心射頻技術(shù)。這確實(shí)像兩個(gè)不等效電阻之間的濾波器設(shè)計(jì)(每種設(shè)計(jì)方案都有其伴隨的想像部份需要加以考慮)。一般是用L和C來(lái)完成的,而非體積龐大、成本高昂的變壓器。除了微波頻段外,其中的變壓器體積不大、價(jià)格也不高,不過(guò)當(dāng)導(dǎo)體靠得太近的時(shí)候,就會(huì)造成諧振波峰。
現(xiàn)在回到我們最初討論的問(wèn)題。為什么一個(gè)(正確設(shè)計(jì)的)雙端接濾波器具有如此優(yōu)越的‘靈敏度’特性?這是因?yàn)閷?duì)于濾波器通帶內(nèi)的一個(gè)或者有時(shí)多個(gè)頻率,它工作在功率傳輸?shù)淖畲罂赡茳c(diǎn)上。請(qǐng)?jiān)俅斡^察圖6和圖7。在雙端接濾波器情況下,元件值的任何變化只會(huì)讓功率傳輸(隨之為電壓增益)下降而非上升。在被稱為反射零點(diǎn)的特定關(guān)鍵頻率上,濾波器響應(yīng)的‘靈敏度’與網(wǎng)路中每個(gè)反應(yīng)元件呈拋物線函數(shù)的下行關(guān)係。這樣就很難讓網(wǎng)路的響應(yīng)比沒(méi)有應(yīng)用功率傳輸約束時(shí)更差。后者狀況指的是單端接的時(shí)候,或者任何濾波器的設(shè)計(jì)響應(yīng)未能滿足最大功率增益值的時(shí)候。要得到最高功率增益值,可以拋開(kāi)濾波器,使用變壓比較為合適的理想變壓器。
還有一個(gè)問(wèn)題。我們?cè)陂_(kāi)始的時(shí)候曾經(jīng)比較過(guò)兩種濾波器,其中一種濾波器的負(fù)載電阻與來(lái)源電阻相等,另一個(gè)則沒(méi)有負(fù)載電阻。我們能否針對(duì)在特定來(lái)源電阻和負(fù)載電阻的比率下成功設(shè)計(jì)出低靈敏度、相同頻率響應(yīng)的濾波器?有時(shí)候是可行的,但至于我們的低導(dǎo)通濾波器案例則不能。對(duì)于特定的響應(yīng),我們需要平坦的響應(yīng),讓DC增益與那些‘觸點(diǎn)’最大值相等。這就意味著在該極低靈敏度的濾波器中,來(lái)源電阻和負(fù)載電阻必須等值。對(duì)于更加普遍的情況而



評(píng)論