嵌入式圖像采集系統的JPEG算法改進

首先離散余弦變換可以通過離散傅里葉變換來實現，其公式如下：

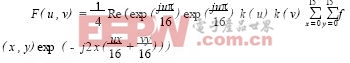
其中Re()為求實部，u，v的取值范圍是0～7。并且對于二維的離散傅里葉變換可使用連續的一維的傅里葉變換來實現，即將傅里葉變換核

寫成

其中在8×8的圖像子塊中M，N均為8。在用離散傅里葉變換計算離散余弦變換時需要將序列擴展為偶序列，而對于偶序列的函數可以表示為傅里葉級數：

令cosx=t，由三角函數的恒等變換得：
cos2x=2cos2x-1
cos3x=4cos3x-3cosx
……

從而可得：

由此可知，括弧中的因式恰好滿足Chebychev多項式T(n，t)=2xT(n-1，t)-T(n-2，t)。該多項式具有良好的遞歸性和正交性，并且其展開式的收斂性良好，可以通過一般性的冪函數

來說明。因為函數e-x在(-∞，+∞)內收斂，所以對于x在任意區間[a，b]，均可以通過公式y=(2x-b- a)/(b-a)將其映射到[-1，1]。當我們取前4項時使用Cheby2chev多項式展開的最大誤差為0。0073444，上式的最大誤差為0。 0516152，因此用它來表示函數可以使用較少的數據項，達到較高的精度，從而在變換域可以選擇更少的系數構成量化碼表的編制，減少數據的傳輸量，提高圖像的壓縮比。

實驗結果及分析

圖2中的a)和b)分別是算法改進前后的圖像的比較。改進前對一幅230456字節320×240的BMP圖像，進行壓縮后得到一幅26951字節的 JPEG圖像，壓縮比約為8.5∶1；而改進后得到的一幅8107字節的圖像，壓縮比約為28∶1，可見壓縮比大大提高。

a) 算法改進前的壓縮圖像　　b) 算法改進后的壓縮圖像
圖2 　改進前后壓縮圖像的比較

結論

對于32 位的嵌入式系統,在應用于圖像采集，特別是遠程的圖像采集時，因處理器足以完成復雜的運算，可以使用改進的JPEG算法，以獲取更高的圖像壓縮比，從而提高圖像數據在網絡上的傳輸速度。