戴維南定理和諾頓定理

一、戴維南定理

圖2-7-1

二端網絡也稱為一端口網絡，其中含有電源的二端網絡稱為有源一端口網絡，不含電源的二端網絡稱為無源一端口網絡，它們的符號分別如圖2-7-1（a）（b）所示。

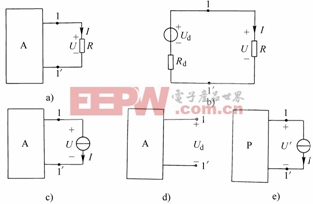
圖2-7-2

任一線性有源一端口網絡（如圖2-7-2（a）所示）對其余部分而言，可以等效為一個電壓源和電阻相串聯的電路（如圖2-7-2（b）所示），其中的大小等于該有源一端口網絡的開路電壓，電壓源的正極與開路端高電位點對應；等于令該有源一端口網絡內所有獨立源為零（即電壓源短接、電流源開路）后所構成的無源一端口網絡的等效電阻。這就是戴維南定理，也稱為等效電源定理；與串聯的電路稱為戴維南等效電路。

要計算一個線性有源一端口網絡的戴維南等效電路，其步驟和方法為：

1、計算：利有電路分析方法，計算相應端口的開路電壓；

2、計算：當線性有源一端口網絡A中不含受控源時，令A內所有獨立電源為零后得到的無源一端口網絡P則為純電阻網絡，利用無源一端口網絡的等效變換就可求出端口等效電阻；當線性一端口網絡A中含有受控源時，令A內所有獨立電源為零后得到的一端口網絡P中仍含有受控源，這時，可采用加壓法和開路短路法求。

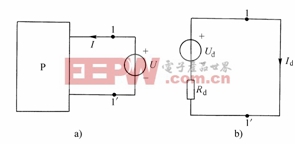
圖2-7-3

例2-7-1 利用戴維南定理求圖2-7-4（a）所示電路中的電流I為多少？

圖2-7-4 例2-7-1附圖

解：將A、B左邊部分電路看作有源一端口網絡，用戴維南等效電路替代后如圖2-10-4（b）所示。

（1）求：將A、B端口開路，得到圖2-10-4（c）所示電路。

由米爾曼公式得：

（2）求等效電阻：令A、B以左的三個獨立源為零，得到圖2-10-4（d）所示電路，則A、B端口的等效電阻為：

（3）從圖2-10-4（b）中求I：

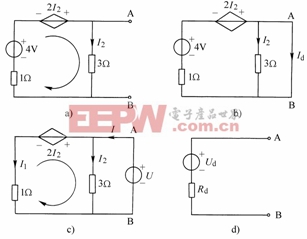
圖2-7-5 例2-7-2附圖

例2-7-2 在圖2-7-5（a）所示電路中，已知，，求A、B端口的戴維南等效電路。

解：（1）求：圖2-10-5（a）中A、B端口處于開路狀態，列寫KVL方程：

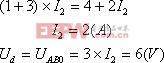
（2）求等效電阻：下面分別用兩種方法求解。

（i）開路短路法：開路電壓已在（1）中求得，現求A、B端口的短路電流。將A、B端口短接，如圖2-10-5（b）所示，從圖中易看出：

， 即

則受控源則有：

，

（ii） 加壓法：將獨立電壓源置零后，然后再在A、B端口加上一個電壓源，如圖2-10-5（c）所示。

列寫KVL方程： ，，又因為：

所以：

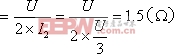
最后，得到A、B端口的戴維南等效電路如圖2-7-5（d）所示。

二、最大功率的傳輸條件：

當一個線性有源一端口網絡化為戴維南等效電路后，在其端口接上可變電阻R，如圖2-10-6所示。當已知，那么當R為多少時它能獲得最大功率？獲得的最大功率又為多少？

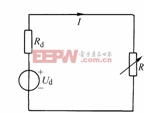
圖2-10-6

令，得到：（式2-10-1 ）

此時 （式2-10-2）

（式2-10-1）就是最大功率的傳輸條件。若是信號源內阻，R是負載電阻，則當滿足最大功率傳輸條件時，傳輸效率為50%，即有一半功率消耗在信號源內阻上。

例2-7-3 在圖2-7-7（a）所示電路中，兩個有源一端口網絡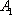、串聯后與R相連，R從改變，測得時，；時，。

（1）當R為多少時，能獲得最大功率？

（2）當將圖2-7-7（b）所示電路代替R接于A、B端口時，，VCVS的控制系數，求端口電壓。

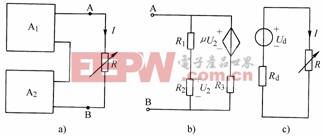
圖2-7-7例2-7-3附圖

解：（1）首先將兩個有源一端口網絡化為戴維南等效電路，分別記為、、、，再將、等效為一個電壓源，記為，將串聯的、等效為一個電阻，于是串聯的兩個有源一端口網絡最后等效為一個電壓源和一個電阻的串聯，如圖2-7-7（c）所示。

代入已知條件： ，

解之得：

所以當時，獲得最大功率：

（2）將圖2-7-7（b）所示電路接于A、B端口，利用節點電壓法，由米爾曼公式得：

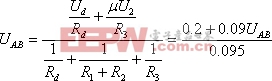
其中：

最后得到：

三、諾頓定理

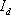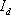任一線性有源一端口網絡（如圖2-7-8（a）所示）對其余部分而言，可以等效為一個電流源與一個電阻相并聯的電路（如圖2-7-8（b）所示），其中的大小等于有源一端口網絡端口的短路電流，電流的方向從高電位點流出；等于戴維南定理中的，即等于令有源一端口網絡內所有獨立源為零后所構成的無源一端口網絡的等效電阻。

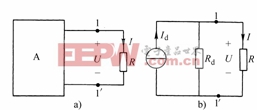
圖2-7-8

要計算一個線性有源一端口網絡A的諾頓等效電路，只要求出網絡A的短路電流、令網絡A中所有獨立源為零后的網絡P的入端等效電阻即可。諾頓定理中的與戴維南定理中的是完全相同的，因此求解方法也完全相同。

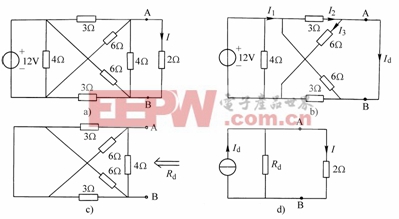
圖2-7-9例2-7-4附圖

例2-7-4 利用諾頓定理計算圖2-7-9（a）所示電路中的電流I。

解：（1）求短路電流：將A、B端口短接，右邊的電阻被短接，得到圖2-7-9（b）所示電路。

（2）求等效電阻：令左邊12V的電壓源為零，左邊電阻被短接，如圖2-7-9（c）所示。

（3）畫出AB端口以左電路的諾頓等效電路，如圖2-7-9（d）所示。

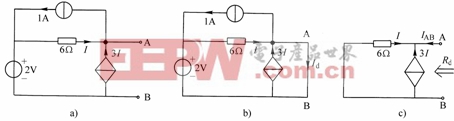
圖2-7-10例2-7-5附圖

例2-7-5 求圖2-7-10（a）所示電路的諾頓等效電路。

解：（1）求短路電流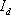：將兩端短接，如圖2-7-10（b）所示。

由KVL有：，

由KCL有： ，

（2） 求A、B端口的等效電阻：令2V的電壓源、1A的電流源為零，受控源仍然保留，得到圖2-7-10（c）所示電路。

，，