組合邏輯電路的分析與設(shè)計(jì)-邏輯代數(shù)
式中 A1,A2,…,An為輸入變量。

組合邏輯電路具有如下特點(diǎn):
(1)輸出、輸入之間沒有反饋延遲通路;
(2)電路中不含記憶單元。
第一節(jié) 邏輯代數(shù)
邏輯代數(shù)亦稱為布爾代數(shù),其基本思想是英國數(shù)學(xué)家布爾于1854年提出的。1938年,香農(nóng)把邏輯代數(shù)用于開關(guān)和繼電器網(wǎng)絡(luò)的分析、化簡,率先將邏輯代數(shù)用于解決實(shí)際問題。經(jīng)過幾十年的發(fā)展,邏輯代數(shù)已成為分析和設(shè)計(jì)邏輯電路不可缺少的數(shù)學(xué)工具。
邏輯代數(shù)提供了一種方法,即使用二值函數(shù)進(jìn)行邏輯運(yùn)算,這樣
,一些用語言描述顯得十分復(fù)雜的邏輯命題,使用數(shù)學(xué)語言后,就變成了簡單的代數(shù)式。邏輯電路中的一個邏輯命題,不僅包含肯定和否定兩重含義,而且包含條件與結(jié)果許多種可能的組合。比如,一個3輸入端的與非門存在著輸入與輸出狀態(tài)的八種可能的組合。用語言描述既嚕嗦又不清晰,用真值表則一目了然,而用代數(shù)式L=ABC表達(dá)就更為簡明。
邏輯代數(shù)有一系列的定律和規(guī)則,用它們對數(shù)學(xué)表達(dá)式進(jìn)行處理
,可以完成對電路的化簡、變換、分析和設(shè)計(jì)。
一、邏輯代數(shù)的基本定律和恒等式
常用邏輯代數(shù)定律和恒等式表:
表中的基本定律是根據(jù)邏輯加、乘、非三種基本運(yùn)算法則,推導(dǎo)出的邏輯運(yùn)算的一些基本定律。
對于表中所列的定律的證明,最有效的方法就是檢驗(yàn)等式左邊的函數(shù)與右邊函數(shù)的真值表是否吻合。
例如,要證明A+A=A時,可按照下面的步驟進(jìn)行證明:
1. 令A(yù)=1,則A+A=l+l=l=A;
2. 令A(yù)=0,則A+A=0+0=0=A;
除此之外,別無其他可能,可見A+A=A。
恒等式可以用其他更基本的定律加以證明,我們來證明其中的第一條,即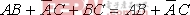
證明如下: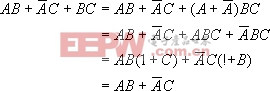
在以上所有定律中,反演律具有特殊重要的意義。反演律又稱為摩根定律,它經(jīng)常用于求一個函數(shù)的非函數(shù)或者對邏輯函數(shù)進(jìn)行變換
。
例1:證明反演律(摩根定律)成立
證明:
因?yàn)椤拜斎攵际牵睍r,輸出才是1”同“輸入有0時,輸出為0”在邏輯上是等效的,這種等效關(guān)系可寫成
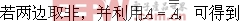

本節(jié)所列出的基本公式反映了邏輯關(guān)系,而不是數(shù)量之間的關(guān)系
,在運(yùn)算中不能簡單套用初等代數(shù)的運(yùn)算規(guī)則。如初等代數(shù)中的移項(xiàng)規(guī)則就不能用,這是因?yàn)檫壿嫶鷶?shù)中沒有減法和除法的緣故。這一點(diǎn)在使用時必須注意。
二、邏輯代數(shù)的基本規(guī)則
1.代入規(guī)則
在任何一個邏輯等式中,如果將等式兩邊出現(xiàn)的某變量A ,都用一個函數(shù)代替,則等式依然成立,這個規(guī)則稱為代人規(guī)則。
例如 ,在B(A+C)=BA+BC中 ,將所有出現(xiàn)A的地方都代以函數(shù)A+D,則等式仍成立,即得B[(A+D)+C]=B(A+D)+BC=BA+BD+BC
代人規(guī)則可以擴(kuò)展所有基本定律的應(yīng)用范圍。
2.反演規(guī)則
根據(jù)摩根定律,求一個邏輯函數(shù)L的非函數(shù)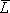 時,可以將L中的與(·)換成或(+),或(+)換成與(·);再將原變量換為非變量(如A換成
時,可以將L中的與(·)換成或(+),或(+)換成與(·);再將原變量換為非變量(如A換成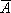 ),非變量換為原變量;并將1換成0,0換成1;那么所得邏輯函數(shù)式就是
),非變量換為原變量;并將1換成0,0換成1;那么所得邏輯函數(shù)式就是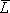 。這個規(guī)則稱為反演規(guī)則。
。這個規(guī)則稱為反演規(guī)則。
注意,交換時要保持原式中的先后順序,否則容易出錯。
例如,求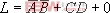 的非函數(shù)
的非函數(shù)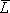 時,按照上述法則 ,可得
時,按照上述法則 ,可得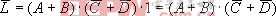 ,不能寫成
,不能寫成 。
。
運(yùn)用反演規(guī)則時必須注意兩點(diǎn):
(1)保持原來的運(yùn)算優(yōu)先順序,即如果在原函數(shù)表達(dá)式中,AB之間先運(yùn)算,再和其他變量進(jìn)行運(yùn)算,那么非函數(shù)的表達(dá)式中,仍然是AB之間先運(yùn)算。
(2)對于反變量以外的非號應(yīng)保留不變。
3.對偶規(guī)則
L是一個邏輯表達(dá)式,如把L中的與(·)換成或(+),或(+)換成與(·);1換成0,0換成1,那么就得到一個新的邏輯函數(shù)式,這就是L的對偶式,記作L。
例如,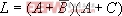 ,則
,則 。變換時仍需注意保持原式中先與后或的順序。
。變換時仍需注意保持原式中先與后或的順序。
所謂對偶規(guī)則,是指當(dāng)某個邏輯恒等式成立時,則其對偶式也成立。
利用對偶規(guī)則,可從已知公式中得到更多的運(yùn)算公式。
例如,吸收律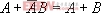 成立,則它的對偶式
成立,則它的對偶式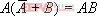 也是成立的。
也是成立的。
三、邏輯函數(shù)的代數(shù)變換與化簡法
在第1章,曾經(jīng)通過列寫真值表,得到了樓梯照明燈控制的邏輯表達(dá)式,它是一個同或函數(shù)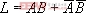 。那么 ,對應(yīng)唯一的真值表,邏輯函數(shù)表達(dá)式和實(shí)現(xiàn)它的邏輯電路是不是唯一的呢?下面就討論這個問題。
。那么 ,對應(yīng)唯一的真值表,邏輯函數(shù)表達(dá)式和實(shí)現(xiàn)它的邏輯電路是不是唯一的呢?下面就討論這個問題。
1.邏輯函數(shù)的變換
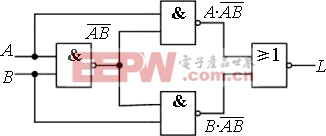
例:函數(shù) 對應(yīng)的邏輯圖如下圖所示。利用邏輯代數(shù)的基本定律對上述表達(dá)式進(jìn)行變換。
對應(yīng)的邏輯圖如下圖所示。利用邏輯代數(shù)的基本定律對上述表達(dá)式進(jìn)行變換。
解: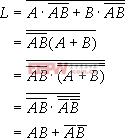
結(jié)果表明,圖示電路也是一個同或門。
例:求同或函數(shù)的非函數(shù)。
解:
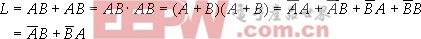
這個函數(shù)稱為異或函數(shù),它表示當(dāng)兩個輸入變量取值相異(一個為0,另一個為1)時,輸出函數(shù)值為1。
在MOS門電路中 ,我們已接觸過異或門,上面的推導(dǎo)更明確地告訴我們,異或門和同或門互為非函數(shù)。所以在異或門電路的輸出端再加一級反相器,也能得到同或門,如下圖所示。
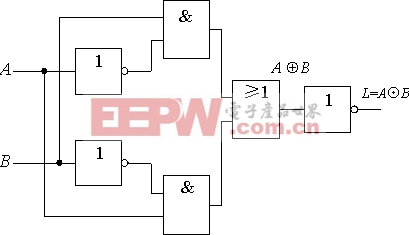
至此,我們已經(jīng)學(xué)到了不止一種同或函數(shù),但是同或函數(shù)的真值表卻是唯一的,事實(shí)上還可以列舉許多。由此可以得出結(jié)論:一個特定的邏輯問題,對應(yīng)的真值表是唯一的,但實(shí)現(xiàn)它的電路多種多樣。這給設(shè)計(jì)電路帶來了方便,當(dāng)我們手頭缺少某種邏輯門的器件時,可以通過函數(shù)表達(dá)式的變換,避免使用這種器件而改用其他器件。這種情形在實(shí)際工作中常會遇到。
2.邏輯函數(shù)的化簡
根據(jù)邏輯表達(dá)式,可以畫出相應(yīng)的邏輯圖。但是直接根據(jù)某種邏輯要求而歸納出來的邏輯表達(dá)式及其對應(yīng)的邏輯圖,往往并不是最簡的形式,這就需要對邏輯表達(dá)式進(jìn)行化簡。
一個邏輯函數(shù)可以有多種不同的邏輯表達(dá)式,如與—或表達(dá)式、或—與表達(dá)式、與非—與非表達(dá)式、或非—或非表達(dá)式以及與—或—非表達(dá)式等。

以上五個式子是同一函數(shù)不同形式的最簡表達(dá)式。以下將著重討論與或表達(dá)式的化簡,因?yàn)榕c或表達(dá)式易于從真值表直接寫出,且只需運(yùn)用一次摩根定律就可以從最簡與或表達(dá)式變換為與非一與非表達(dá)式,從而可以用與非門電路來實(shí)現(xiàn)。
最簡與或表達(dá)式有以下兩個特點(diǎn):
①與項(xiàng)(即乘積項(xiàng))的個數(shù)最少。
②每個乘積項(xiàng)中變量的個數(shù)最少。
代數(shù)法化簡邏輯函數(shù)是運(yùn)用邏輯代數(shù)的基本定律和恒等式進(jìn)行化簡,常用下列方法:
① 并項(xiàng)法

② 吸收法

③ 消去法
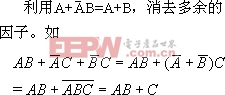
④ 配項(xiàng)法

使用配項(xiàng)的方法要有一定的經(jīng)驗(yàn),否則越配越繁。通常對邏輯表達(dá)式進(jìn)行化簡,要綜合使用上述技巧。以下再舉幾例。
例1 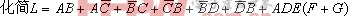
解:

例2 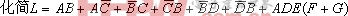












評論