Mathematica入門教程之Mathematica的基本語法特征
加入技術交流群
Mathematica還有各種表達式操作的函數，如取分子、分母的 Numerator[expr] , Denormator[expr],取系數的Coefficient[expr],因式分解的Factor[expr],以及展開的Expand[expr]和ExpandAll[expr],表達式化簡的Simplify[expr]等。expr代表一個任意的表達式。
. 求極限
計算函數極限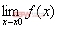
的一般形式是:
Limit[expr,x->x0] x->x0時函數的極限
Limit[expr,x->x0,Direction->-1] x->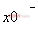
時函數的極限
Limit[expr,x->x0, Direction->1] x->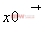
時函數的極限
In[1]:=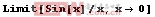
Out[1]:=1
. 微商和微分
在Mathematica中能方便地計算任何函數表達式的任意階微商(導數).如果f是一元函數,D[f,x]表示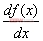
;如果f是多元函數,D[f,x]表示
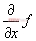.微商函數的常用形式如下:
D[f,x]
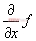
In[1]:=D[x^x,x]
Out[1]:=
下面列出全微分函數Dt的常用形式及其意義:
Dt[f] 全微分
Dt[f,x] 全導數
Dt[f,x1,x2,…] 多重全導數
In[1]:=Dt[x^2+y^2]
Out[1]:=
. 不定積分和定積分
- 不定積分
Integreate函數主要計算只含有1“簡單函數”的被積函數. “簡單函數”包括有理函數、指數函數、對數函數和三角函數與反三角函數。不定積分一般形式如下：
Integrate[f，x] 計算不定積分
Integrate[f，x，y] 計算不定積分
Integrate[f，x，y，z] 計算不定積分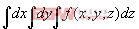
In[1]：=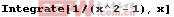
評論