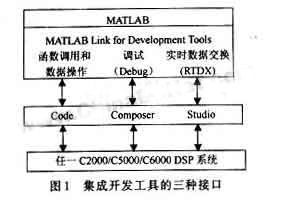
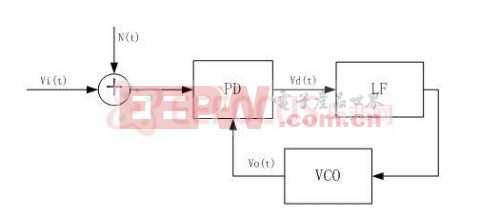
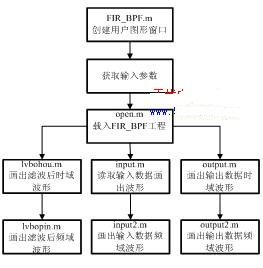
MATLAB入門教程之數值分析
ans= -cos(a)
>>int(S3)
ans= 2/3*x^(3/2)
>>int(S3,'a','b')
ans= 2/3*b^(3/2)- 2/3*a^(3/2)
>>int(S3,0.5,0.6)
ans= 2/25*15^(1/2)-1/6*2^(1/2)
>>numeric(int(S3,0.5,0.6)) % 使用numeric函數可以計算積分的數值
ans= 0.0741
2.3求解常微分方程式
MATLAB解常微分方程式的語法是dsolve('equation','condition'),其中equation代表常微分方程式即y'=g(x,y),且須以Dy代表一階微分項y' D2y代表二階微分項y'' ,
condition則為初始條件。
假設有以下三個一階常微分方程式和其初始條件
y'=3x2, y(2)=0.5
y'=2.x.cos(y)2, y(0)=0.25
y'=3y+exp(2x), y(0)=3
對應上述常微分方程式的符號運算式為:
>>soln_1 = dsolve('Dy = 3*x^2','y(2)=0.5')
ans= x^3-7.500000000000000





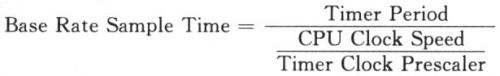

評論