CAN調度理論與實踐分析

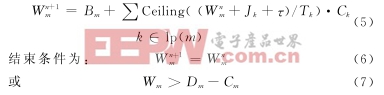
　　式(7)代表最壞等待時間已超時限，消息m不可調度。

　　按優先級降低的次序逐條校驗消息是否可調度，就可驗證整個通信系統是否可調度。

　　在2006年實時網絡會議上，Bril、Davis等人發表了有關Tindell算法有漏洞的文章，后來他們又提出了完整的改進算法[4]。作為反例，表1中消息C用Tindell算法是可調度的，最壞響應時間為3 ms；但第2次消息C的傳送已超時限，如圖2所示。Tindell算法僅考慮了消息C的第1次傳送。

表1 Tindell算法的反例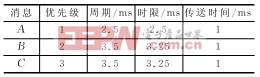

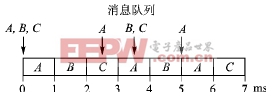
圖2 消息C的最壞響應時間為3.5 ms

　　另外，如將消息B和C的周期縮短為3.25 ms，按照Tindell算法，系統由于未求得最大的最壞響應時間，故仍是可調度的，但實際上總線的利用率已超過100%。Davis的方法核心是引入忙周期的概念，再對忙周期內各次傳送的響應時間求最壞值，詳見附錄1。（見本刊網站www.mesnet.com.cn——編者注。）

　　Tindell的開創性工作對后續的研究與應用有巨大的影響，Volcano通信技術公司(現在的Mentor Graphics)以此理論為基礎開發了商用的CAN調度分析軟件。由于漏洞的發現，用戶應檢驗軟件是否有了新的補丁以及用它完成的應用是否受影響。

2 筆者對Davis算法的簡化

　　Davis算法要先算出忙周期，再在忙周期中消息m多次傳送中尋找最壞等待最大的那次。基于以下考慮，計算可以簡化：

　　在忙周期中，消息m傳送時有高優先級消息進入隊列，使m的后續消息發送前可能插入更多的高優先級消息，代表仍有一個對總線需求的高峰，從而有可能使后面的消息m有更大的最壞響應時間。

　　最壞的情形是消息m剛發送，所有高優先級消息就進入隊列，即領先于發完消息m后的第一個發送空隙的相位達到最大。

　　因此求消息m的最壞響應時間就有兩種可能： 用Bm產生阻塞，像Tindell那樣求消息m的最壞響應時間；由Cm產生阻塞，求下一個消息m的最壞響應時間，下一個消息m的排隊時間為Tm-Jm。

　　簡化方法的優點是減少了計算的次數，從而減少工作量。

　　這種算法與Davis算法中的保守算法有兩點不同：一是用Cm來產生阻塞是真實可能發生的，例如從休眠到上電時消息m比高優先級消息早了一點；二是本算法得到的是確切的而非保守的結果。