干擾噪聲系統基礎知識

　　任何電子系統都存在許多噪聲來源。表現形式主要有三種：發射噪聲，與原始信號一起接收且無法區分;內生噪聲(例如發熱產生的約翰遜噪聲、散粒噪聲和爆米花噪聲)，源自構成電路的器件;以及干擾噪聲，從電路外部拾取。干擾噪聲可能源于自然干擾(如閃電)，或者從系統內或附近的其他電氣設備(例如電腦、開關電源、SCR控制加

　　熱器、無線電發射機、開關觸點等)耦合進來。

　　本文僅探討最后一類，即人為噪聲，這是數據采集或測試系統中最普遍存在的系統噪聲。它在低電平電路中最麻煩，系統任何部分均無法逃脫其影響。但它也是會受布線和屏蔽選擇影響的唯一噪聲形式。

　　假設和分析工具

　　盡管完整、精確描述電氣系統特性必然用到麥克斯韋方程組(意味著更多的數學計算)，但大多數情況下傳統的電路分析仍然很有用。解決這些問題時，要確保電路分析有效，需做如下假設：

　　1. 所有電場局限于電容內部。

　　2. 所有磁場局限于電感直接相鄰部分。

　　3. 電路尺寸相對于所考慮的波長較小。

　　使用上述假設，我們可以將噪聲耦合通道模擬為集總電路元件。將耦合兩個電感的磁場模擬為互感?？蓪㈦s散電容模擬為兩個導體，兩者間存在電場。圖1顯示了一個等效電路情況，其中兩根短導線在系統地上彼此相鄰。

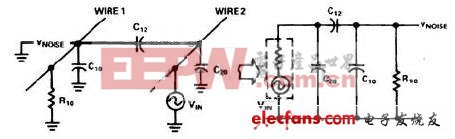
　　圖1. 兩個相鄰導線和接地層的噪聲等效電路。

　　一旦獲得某一系統的完整噪聲等效電路，問題就成為針對所需參數求解其中一個網絡方程式。所有標準線性電路分析技術均可應用，包括節點方程、環路方程、矩陣代數、狀態變量、疊加、拉普拉斯變換等等。當電路超過5和6個節點時，手動計算變得困難;此時必須使用計算機輔助程序，例如SPICE，以及其他CAD技術。有經驗的設計師可以適當地簡化假設;但其有效性在得到驗證前必須始終警惕。

　　集總元件方法不一定給出精確數字答案，但可以清晰顯示噪聲與系統參數的依賴關系。繪制盡可能詳確的等效電路可以給如何降低噪聲電平提供思路。一旦寫出網絡方程和CAD程序，便可研究噪聲抑制技術的定量影響。

　　雖然所有現代技術均在進步，例如微處理器和開關電源，但導線仍具有電阻和電感，電容仍存在于真實世界，這些現象必須認真對待。

　　基本原理

　　噪聲問題始終牽涉三個因素：噪聲源(線路瞬變、繼電器、磁場等)、耦合介質(電容、互感、導線)和接收機，即易受噪聲影響的電路(圖2)。

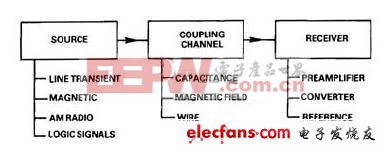
　　圖2. 噪聲拾取始終涉及噪聲源、耦合介質和接收機。

　　要解決問題，必須消除、削弱或轉移這三個因素中的一個或多個。在可以解決問題前，必須徹底弄清這些因素在問題中的作用。如果解決方案不當，噪聲問題只會變得更糟!不同噪聲問題需要不同的解決方案;添加電容或屏蔽體并不一定有效。

　　系統噪聲類型

　　任何電子系統中的噪聲來源很多，包括計算機、風扇、電源、相鄰設備、測試器件，甚至用于抑制噪聲但連接不當的屏蔽體和接地線。我們討論的噪聲源和耦合機制包括下列主題：

　　●公共阻抗噪聲

　　●容性耦合噪聲

　　●磁耦合噪聲

　　●電力線瞬變

　　●其他噪聲源

　　公共阻抗噪聲

　　顧名思義，公共阻抗噪聲是由數個電路共有的阻抗引起的。圖3顯示了基本配置，可能發生于脈沖輸出源和運算放大器基準端子均連接到“接地”點的情況，該點對電源返回端子有明顯阻抗。噪聲電流(電路1的噪聲返回電流)將在阻抗Z兩端產生電壓Vnoise，該電壓對電路2表現為噪聲信號。

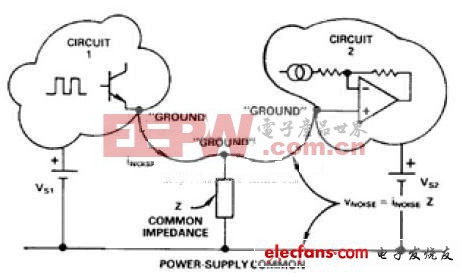
　　圖3. 公共電路阻抗如何產生噪聲。

　　通常，此類噪聲的重復率取決于噪聲源速率。實際波形由阻抗Z的特性決定。例如，如果Z完全是電阻式，噪聲電壓將與噪聲電流成正比，并具有相似形狀(圖4a)。如果Z為R-L-C，噪聲電壓將以頻率1/(2πLC)振鈴，并以L/R (b)確定的速率呈指數性衰減。

　　如果在電路中發現此類噪聲，可以從重復率和波形很容易地推斷出原由。重復率將指向噪聲來源，因為噪聲與其來源是同步的。

　　例如，(c)中所示的噪聲波形(重復率25kHz，占空比25%)就是包含調節環路并使用脈寬調制的開關電源的典型波形。

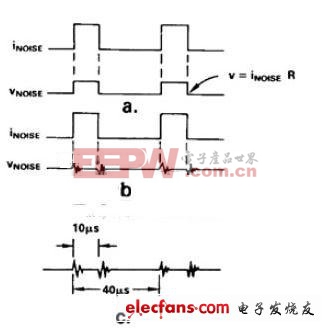
　　圖4. 公共阻抗中的噪聲效應，(a)電阻，(b)R-L-C電路，(c)開關噪聲響應。

波形有助于確定實際產生干擾噪聲的阻抗。例如，如果噪聲波形是圖5所示的簡單阻尼正弦波，以下特性可幫助我們推斷Z的性質：

　　● 恒定電阻R與線路串聯。電壓變化V1是R與電流階躍I1的

　　乘積。

　　●振蕩自然頻率f1取決于串聯的L和并入的C，f = 1/(2πLC)。

　　●阻尼時間常數T由L/R決定。

　　圖5. 欠阻尼R-L-C電路的波形。

　　容性耦合噪聲

　　噪聲源至另一電路的容性耦合也會產生噪聲。此類噪聲常見于具有快速升降時間或高頻成分的信號靠近高阻抗電路的情況。雜散電容將信號快速沿耦合至相鄰電路，如圖6的電路模型所示。阻抗Z的性質決定響應波形。表1列出了典型電容。

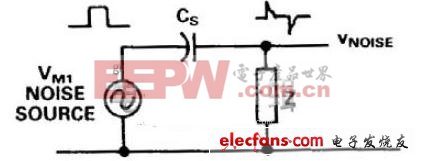
　　圖6. 雜散電容將噪聲耦合至高阻抗電路。

　　表1. 典型電容。

　　容性拾取發生的方式、形狀和大小有多種。下面是幾個示例：

　　●TTL數字信號產生快速沿，典型上升時間為10納秒，電壓擺幅為5 V。如果Z是1兆歐電阻，即使0.1pF也會產生5 V尖峰和100納秒的衰減時間常數。

　　●兩根相鄰導線間可能產生串擾。例如，如果兩根導線是10英尺(3米)長度的電纜，電容為40 pF/英尺，則總電容為400 pF。如果在一個導體上施加1 kHz的10 V測試電壓，當Z是10 k電阻時，1 kHz的250 mV電壓將耦合至相鄰導線。

　　●通過公共阻抗在交流電力線上產生的噪聲將耦合至其他電路。常見情況是瞬變通過電源變壓器的繞組間電容耦合。

　　令人驚奇的是，小小的電容竟能導致嚴重問題。例如，考慮高抗擾度CMOS邏輯用于工業電路中的情況，電路中存在2500 V、1.5 MHz噪聲瞬變(IEEE標準472-1974)。假設CMOS輸入與噪聲源之間僅有0.1 pF的雜散電容，如圖7所示。計算出的噪聲電壓為2.4 V，穩態下，50 V的初始瞬變將導致邏輯運算錯誤，甚至更壞的情況!

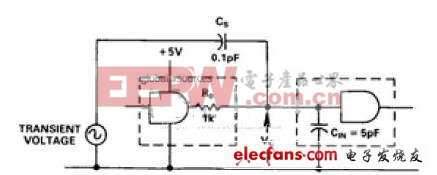
　　圖7. 高壓瞬變從測試發生器耦合至邏輯。

　　磁耦合噪聲

　　電纜載送電流、分配交流電源時，以及機器、電源變壓器、風扇等附近均可發現強磁場。磁耦合電路與容性耦合電路間存在類似的關系，如圖8和表2所示。

　　● 噪聲為磁耦合時，電壓噪聲(Vn)表現為與接收機電路串聯;而在容性情況下，接收機與地電壓間產生的電壓噪聲是噪聲電流in在Z中造成的電壓。

　　●降低接收機阻抗Z可減少容性耦合噪聲。磁耦合電路則不同;降低Z不會顯著減少電壓噪聲。

　　圖8. 磁噪聲耦合與容性噪聲耦合的比較。

　　表2. 容性耦合與磁耦合的特性。