利用1dB壓縮點表征射頻系統(tǒng)非線性

增益壓縮導致電力系統(tǒng)從線性運行過渡到非線性運行。了解如何使用1 dB壓縮點來定義線性操作的限制。

多種機制導致電子系統(tǒng)的非線性。例如，有源器件的跨導受到信號幅度的影響。這些器件內的寄生電容和電阻也與幅度有關，這會影響電路的性能。此外，即使短暫地超過電路的正常信號擺動，也會導致信號波谷或波峰的削波，給系統(tǒng)引入大量的非線性。

在高功率水平下，所有實際組件都表現(xiàn)出非線性。在射頻電路中，這可能會導致?lián)p耗增加、信號失真，并可能對其他無線信道造成干擾。非線性可以用幾種方式來表征，每種方式都為電路在不同條件下如何偏離線性行為提供了獨特的視角。

在這篇文章中，我們將深入研究射頻電路非線性的兩種形式：諧波失真和增益壓縮。我們還將探討1 dB壓縮點，這是表征增益壓縮的有用指標。

1dB壓縮點是什么？

如圖1所示，1dB壓縮點定義為輸出功率比理想線性特性低1dB的功率電平。我們使用此規(guī)范來量化RF電路線性操作的上限。

1dB壓縮點用作量化電路線性度的度量。

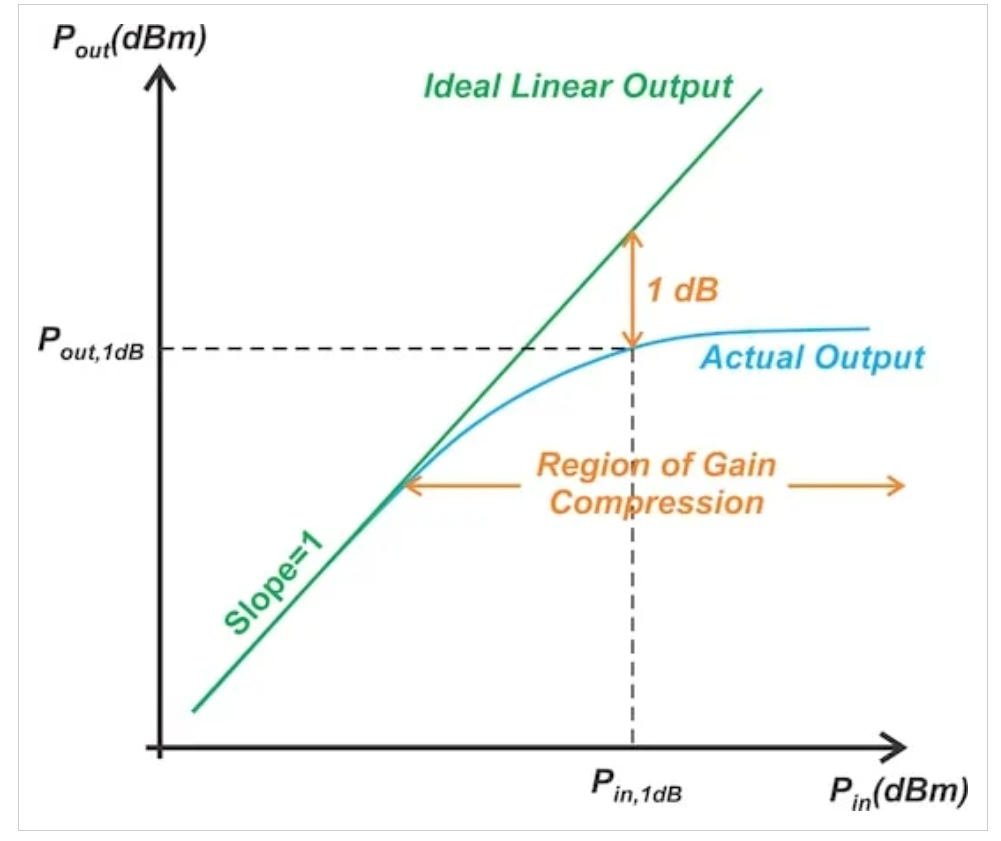
圖1 1dB壓縮點用作量化電路線性度的度量

1dB壓縮點可以用輸入或輸出功率表示：

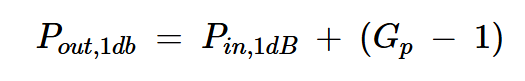
方程式1

其中：

Gp是放大器的理想線性增益，單位為分貝

Pin，1dB是發(fā)生壓縮的輸入功率

Pout，1dB是發(fā)生壓縮的輸出功率。

對于放大器，1 dB壓縮點通常指定為發(fā)生壓縮的輸出功率。對于混音器，通常用與壓縮點對應的輸入功率來表示。RF接收器的輸入壓縮點通常在-20至-25 dBm的范圍內。

現(xiàn)在我們知道1dB壓縮點是什么了，讓我們退一步，更廣泛地考慮非線性系統(tǒng)的行為。本次討論將為我們理解諧波失真和增益壓縮奠定基礎。稍后我們將回到1dB壓縮點。

無記憶非線性系統(tǒng)建模

考慮一個具有輸入x（t）和輸出y（t）的設備或系統(tǒng)，如圖2所示。

通用設備或網絡。

圖2 通用設備或網絡

如果網絡的傳遞特性為：

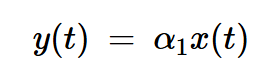
方程式2

其中?1是一個與時間無關的常數(shù)。如果不滿足上述條件，則電路是非線性的。無記憶非線性系統(tǒng)的輸入輸出特性可以用多項式表達式近似：

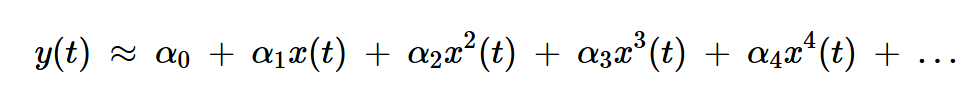
方程式3

我們通常在多項式表達式中保留高達三階的項，導致：

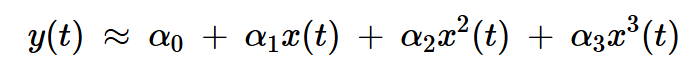
方程式4

請注意，在上述方程中，任何給定時間（t）的輸出瞬時值僅由同一時刻的輸入值決定。此條件定義了一個無記憶特性。如果時間t的輸出受到先前輸入值的影響，則該特性表現(xiàn)出記憶效應。

在有記憶的系統(tǒng)中，時滯輸入或其導數(shù)和積分可能出現(xiàn)在輸出方程中。例如，輸出信號可以是以下列方式依賴于x（t）的函數(shù)：

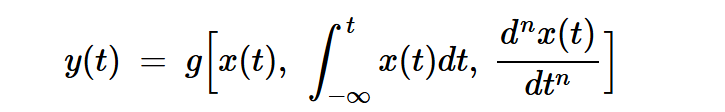
方程式5

諧波失真

多項式近似的非線性特性可以針對單音或雙音輸入進行檢查。讓我們看看如果我們將以下單音輸入應用于方程4的非線性特性會發(fā)生什么：

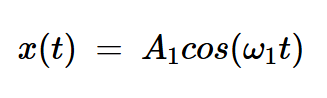
方程式6

我們獲得：

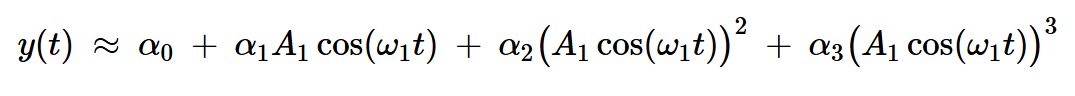
方程式7

二階項產生的輸出信號為：

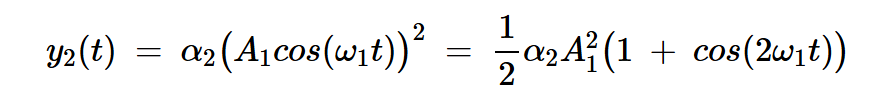
方程式8

二階非線性在直流和二次諧波（2?1）處產生頻率分量。

另一方面，三階項產生：

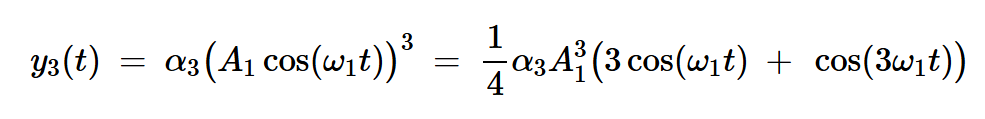
方程式9

三階項產生基頻和三次諧波（3?1）的頻率分量。

結合方程7、8和9，三階傳遞函數(shù)的總輸出信號為：

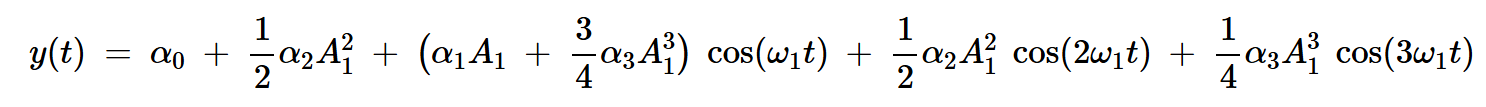
方程式10

當單音輸入為?1時，方程的高階項會在輸入的所有諧波處產生頻率分量。這種現(xiàn)象被稱為諧波失真。

不同諧波下的輸出功率

讓我們假設上述討論中的x（t）和y（t）是電壓量。根據(jù)方程式10，基波電壓分量的振幅為：

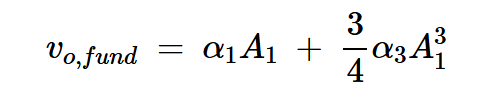
方程式11

?1處的總輸出信號包括兩個不同的項：線性項和三階項。對于低水平的輸入功率，線性項占主導地位。我們暫時忽略三階項。

電阻歸一化為1，基頻下的輸出功率為：

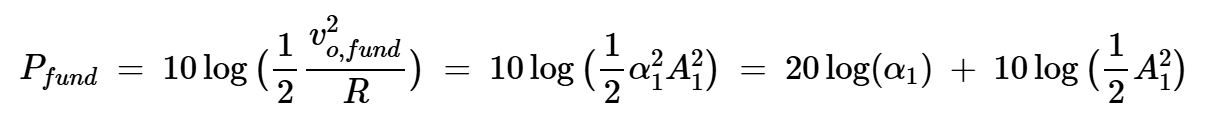
方程式12

上述方程中的最后一項是輸入信號的功率：

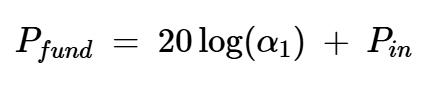
方程式13

這意味著，對于低輸入功率值，輸入功率每增加1dB，基本輸出功率就會增加1dB。

二次和三次諧波分量呢？根據(jù)方程式10，二次諧波的輸出功率為：

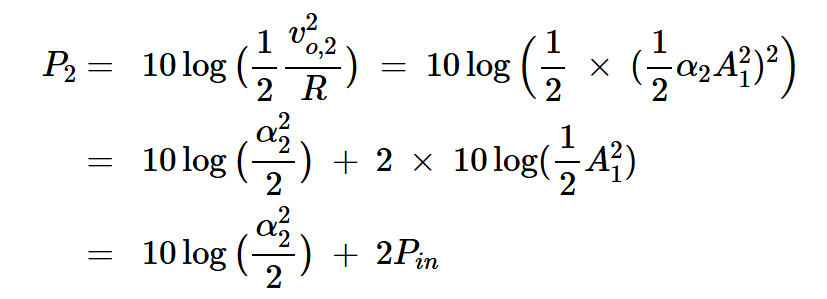
方程式14

因此，輸入功率每增加1dB，二次諧波的輸出功率就會增加2dB。同樣，可以證明，對于三次諧波，輸出功率與輸入功率曲線的斜率為3:1。一般來說，當功率以分貝表示時，n次諧波的功率水平呈現(xiàn)出n:1的斜率。如圖3所示。

不同諧波下的輸出功率與輸入功率。

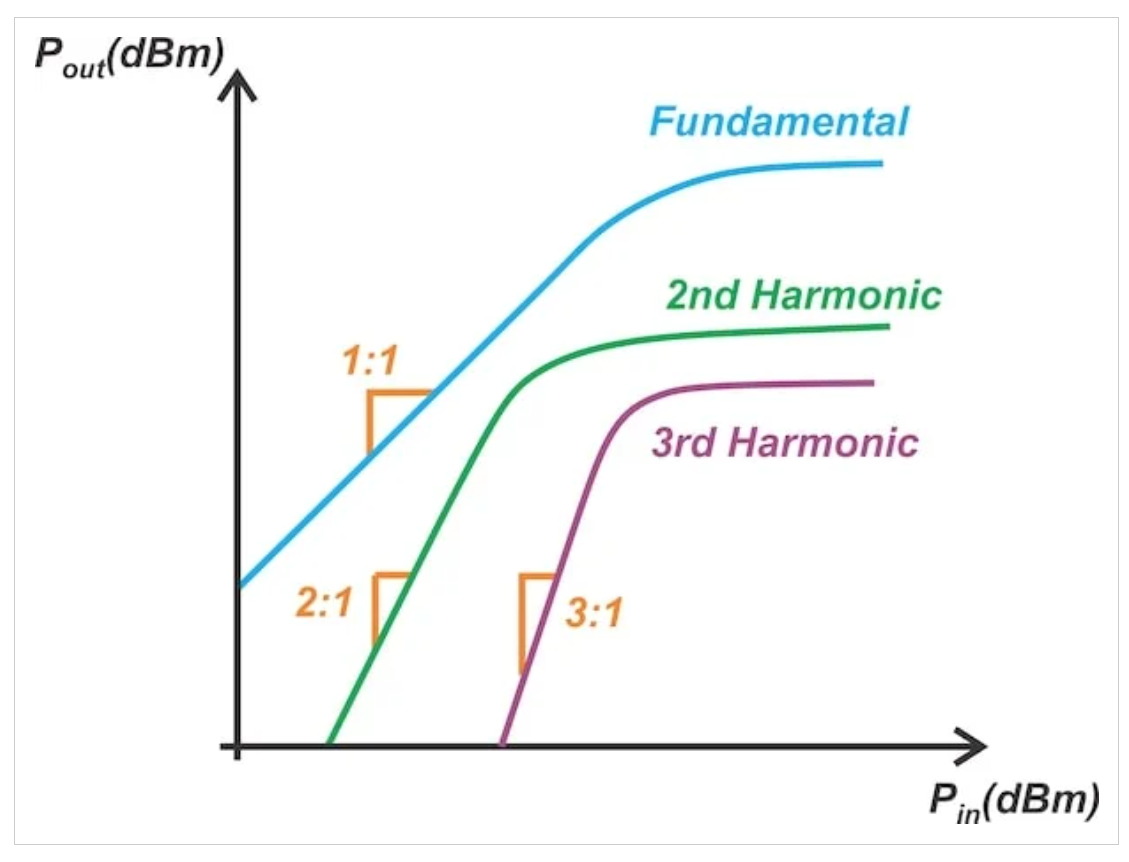
圖3 不同諧波下的輸出功率與輸入功率

在弱非線性區(qū)域，輸入功率每增加1dB，基頻的功率就增加1dB。二次諧波和三次諧波分別上升2 dB和3 dB。

對于在弱非線性區(qū)域之外運行的實際電路，諧波頻率中的功率可能不會相對于輸入功率單調增加。這是由于我們的三次多項式表達式中忽略了高階非線性項的影響。

增益壓縮

在較高的輸入功率下，輸出開始飽和。這意味著輸出功率不再隨輸入功率線性增加。一個原因是電源電壓限制了電路的最大輸出電壓。

圖3顯示，放大器在基頻下的增益取決于輸入功率，并且隨著輸入功率的增加而下降。為了更好地理解這一點，讓我們使用方程10來確定基頻處的增益：

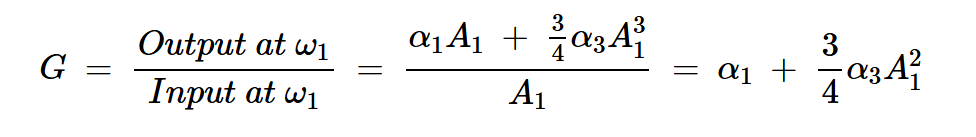
方程式15

在低輸入功率下，?1項占主導地位，使增益等于放大器的小信號增益。然而，隨著輸入信號幅度的增加，上述方程中的第二項迅速增長。

對于大多數(shù)實際電路，?1和9082》3具有相反的符號。因此，在較高功率水平下增益會降低。這種現(xiàn)象被稱為增益壓縮。

確定1 dB壓縮點

使用1dB壓縮點作為度量，我們可以根據(jù)多項式表達式的系數(shù)確定壓縮發(fā)生的信號幅度。應用本文開頭給出的定義，方程15給出的放大器的實際增益比壓縮點處的理想增益（?1）低1 dB。因此，我們有：

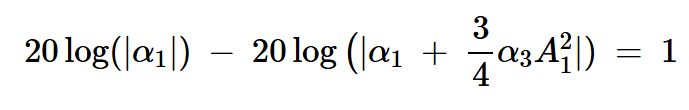
方程式16

其簡化為：

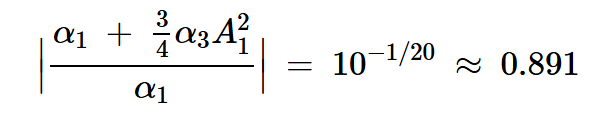
方程式17

最后，我們得到：

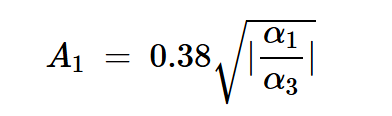
方程式18

這是發(fā)生1dB壓縮的輸入信號幅度。

關鍵要點

即使使用單音輸入，非線性電路也會以輸入頻率的整數(shù)倍產生輸出。這種現(xiàn)象被稱為諧波失真。

此外，對于單音輸入，非線性電路在基頻處的總輸出信號由線性項和三階非線性項組成。在實際電路中，這會產生增益壓縮。

為了量化電路線性區(qū)域的上限，我們使用1dB壓縮點。這被定義為輸出功率比理想線性特性低1dB的功率電平。