Phasors如何幫助我們理解帶通信號(hào)
使用相量,我們探索了在RF通信系統(tǒng)使用的模型中,實(shí)值帶通信號(hào)是如何表示為復(fù)基帶信號(hào)的。
本文引用地址:http://www.104case.com/article/202505/470072.htm帶通信號(hào)和系統(tǒng)在通信系統(tǒng)中至關(guān)重要。有趣的是,實(shí)值帶通信號(hào)中攜帶的所有信息都包含在相應(yīng)的復(fù)值基帶信號(hào)中。這種復(fù)雜的基帶表示對(duì)于理解無(wú)線電通信系統(tǒng)非常有幫助。
在本文中,我們將學(xué)習(xí)帶通信號(hào)的復(fù)基帶表示。作為討論的一部分,我們還將探討交流電路中相量分析的概念。然而,在我們深入探討之前,讓我們通過(guò)回顧低通和帶通信號(hào)的定義來(lái)確保我們已經(jīng)涵蓋了基礎(chǔ)知識(shí)。
低通和帶通信號(hào)
當(dāng)信號(hào)的頻率內(nèi)容或頻譜以零頻率為中心時(shí),該信號(hào)被稱(chēng)為低通信號(hào)。換句話說(shuō),低通信號(hào)具有明確定義的帶寬B,|f|>B的頻譜內(nèi)容可以忽略不計(jì)。
示例低通信號(hào)的頻譜,分為實(shí)部和虛部。
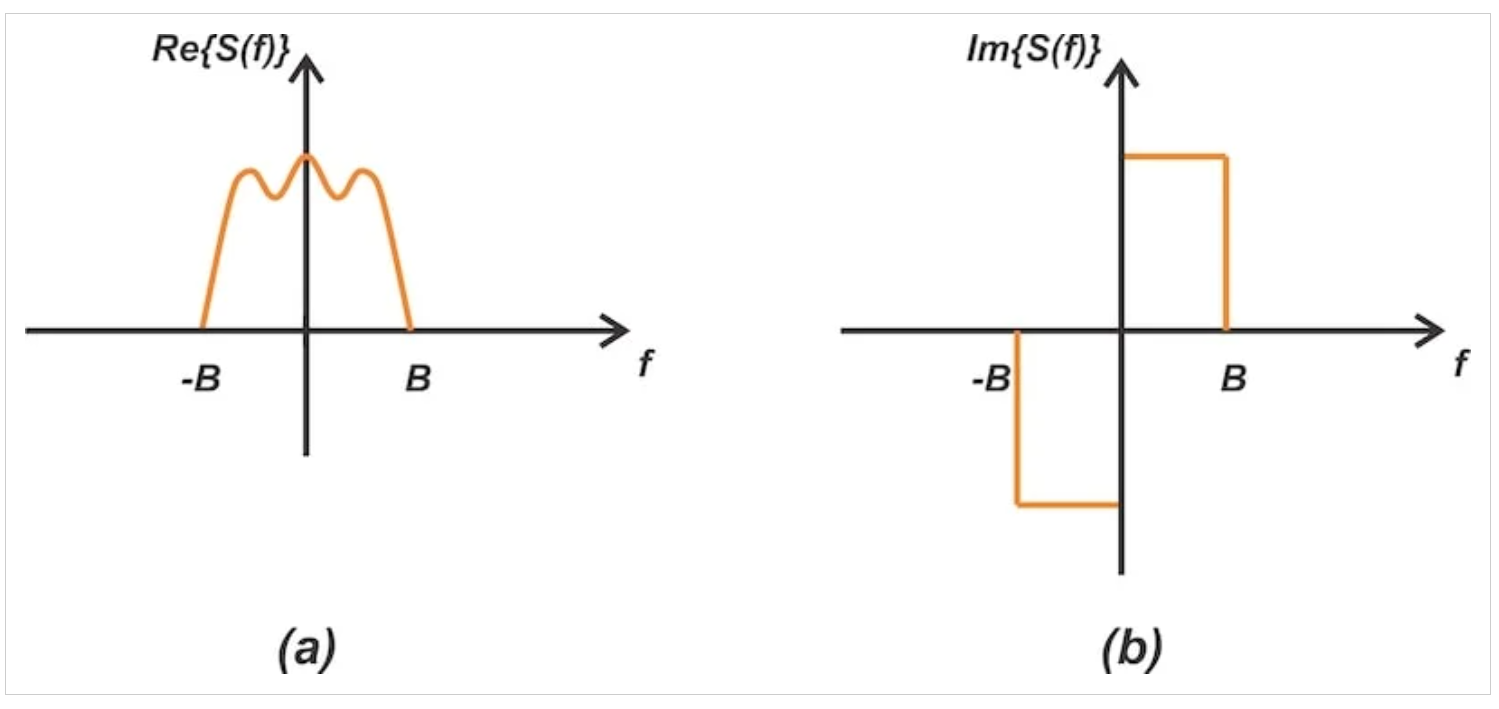
圖1 帶寬為b的實(shí)值低通信號(hào)的實(shí)部(a)和虛部(b)
請(qǐng)注意,如果s(t)是實(shí)值函數(shù),其傅里葉變換(s(f))將表現(xiàn)出共軛對(duì)稱(chēng)性。這意味著S(f)的實(shí)部是偶數(shù)函數(shù),而虛部是奇數(shù)函數(shù)。
另一方面,帶通信號(hào)的頻譜中心頻率(fc)遠(yuǎn)大于信號(hào)帶寬(B)。圖2顯示了示例帶通信號(hào)的實(shí)部和虛部。
以fc為中心的示例帶通光譜的實(shí)部(a)和虛部(b)。
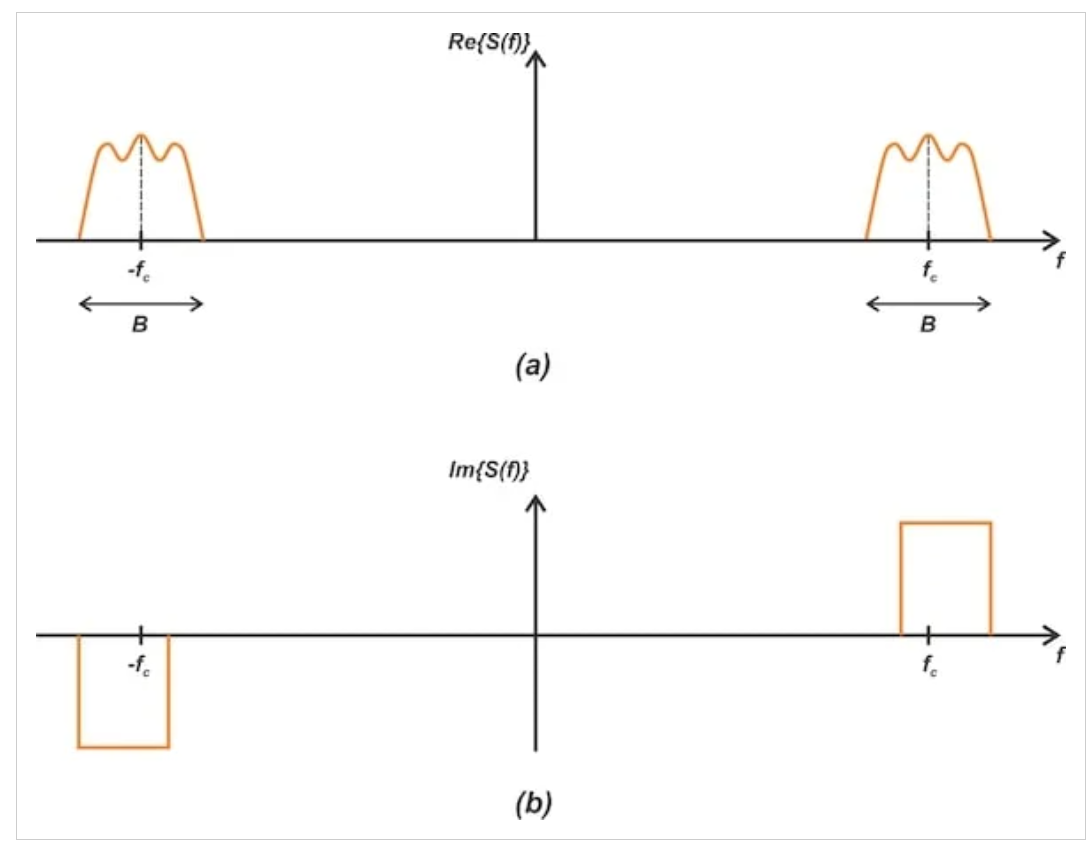
圖2 中心頻率為fc、帶寬為B的實(shí)值帶通信號(hào)的頻譜,分為實(shí)部(a)和虛部(B)
與圖1中的示例基帶頻譜一樣,由于信號(hào)是實(shí)值的,圖2表現(xiàn)出共軛對(duì)稱(chēng)性。
實(shí)信號(hào)的帶寬被定義為信號(hào)中包含的所有正頻率分量的跨度。如果信號(hào)中存在的最高和最低正頻率分別為fmax和fmin,則信號(hào)的帶寬為:
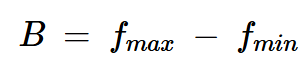
方程式1
根據(jù)上述定義,頻率為fc且振幅a恒定的單音正弦曲線的帶寬為零。
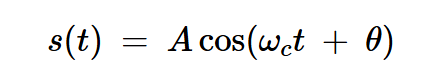
方程式2
然而,如果A隨時(shí)間緩慢變化,那么我們就有一個(gè)非零帶寬的調(diào)幅(AM)波。
交流電路中的相量表示
相量是一個(gè)復(fù)數(shù),表示正弦波形的幅度和相位角。在交流電路分析中,相量用于分析頻率相關(guān)效應(yīng)。
例如,考慮方程2中所示的單音正弦波。該信號(hào)是復(fù)雜函數(shù)的實(shí)部:
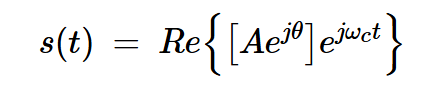
方程式3
其中,運(yùn)算符Re{.}表示花括號(hào)內(nèi)包含的量的實(shí)部。我們可以將花括號(hào)內(nèi)的項(xiàng)表示為復(fù)平面中的向量,其振幅為a,初始相位為θ。如圖3所示,該信號(hào)以角速度?c=2πfc圍繞原點(diǎn)旋轉(zhuǎn)。
單音正弦波的相量表示。
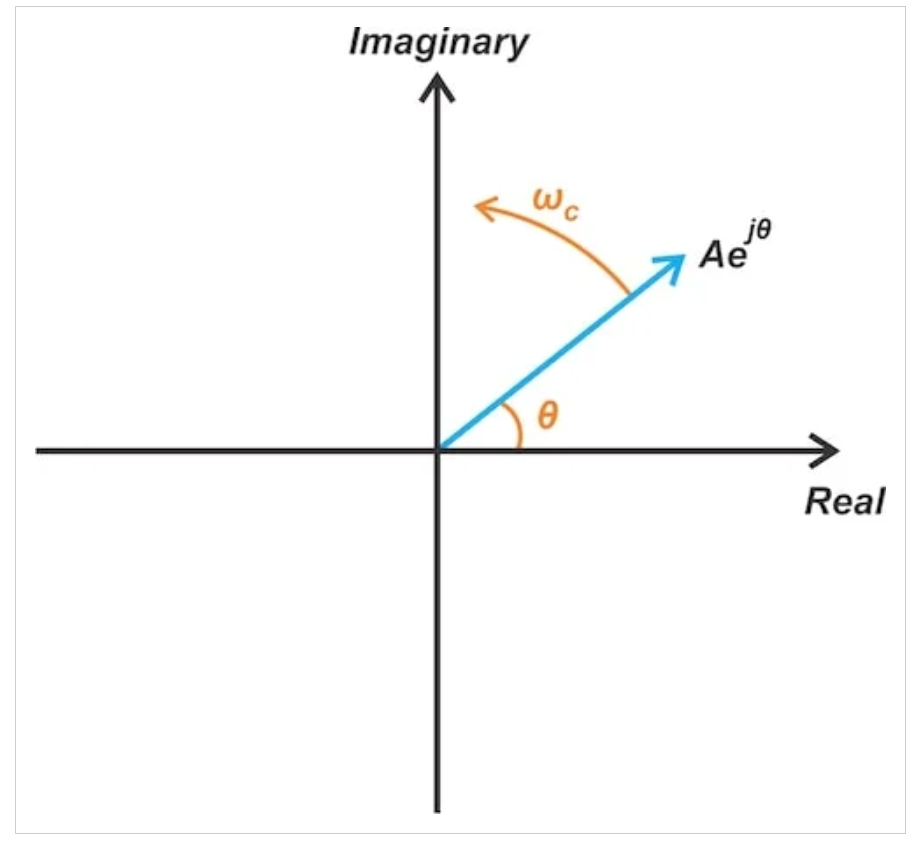
圖3 單音正弦波的相量表示
上述矢量在實(shí)軸(其實(shí)部)上的投影產(chǎn)生方程2所示的原始信號(hào)。角項(xiàng)ωct表示每秒fc轉(zhuǎn)的穩(wěn)定逆時(shí)針旋轉(zhuǎn)。為了獲得信號(hào)的簡(jiǎn)化表示,我們將暫時(shí)忽略此項(xiàng)。
去除旋轉(zhuǎn)導(dǎo)致一個(gè)固定向量,該向量對(duì)應(yīng)于方程3中方括號(hào)內(nèi)的項(xiàng)。這個(gè)與時(shí)間無(wú)關(guān)的術(shù)語(yǔ)是與我們的信號(hào)相關(guān)的相量。它由以下因素給出:
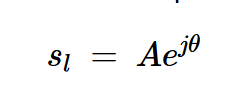
方程式4
為了理解相量表示的意義,考慮一個(gè)由正弦輸入激勵(lì)的線性時(shí)不變(LTI)系統(tǒng)。如圖4所示,這種激勵(lì)在電路內(nèi)的所有節(jié)點(diǎn)上產(chǎn)生正弦信號(hào)。盡管所有這些信號(hào)具有相同的頻率,但它們的幅度和相位可能不同。
LTI電路產(chǎn)生的正弦信號(hào)可以用具有不同幅度和初始相位但以相同角速度旋轉(zhuǎn)的相量來(lái)描述。
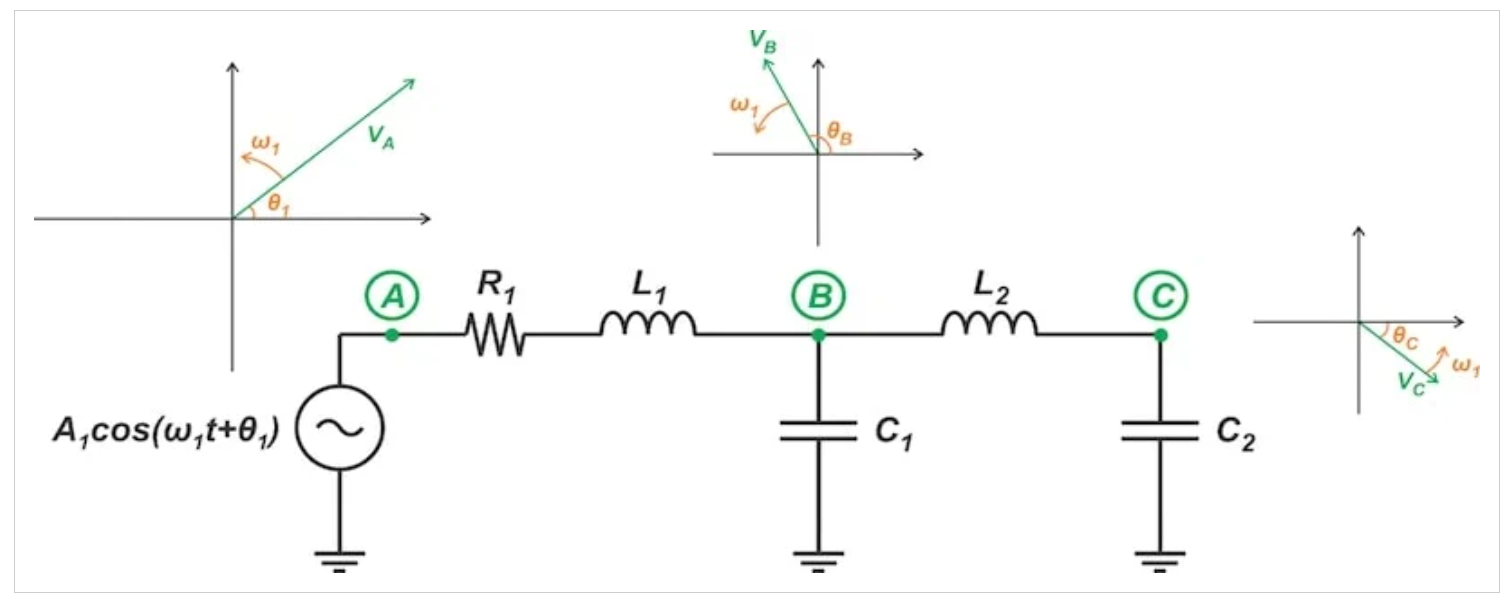
圖4 LTI電路產(chǎn)生的正弦信號(hào)可以用具有不同幅度和初始相位但以相同角速度旋轉(zhuǎn)的相量來(lái)描述
由于所有這些矢量以相同的速度旋轉(zhuǎn),它們之間的相位差不會(huì)隨時(shí)間變化。這些矢量的振幅比同樣與時(shí)間無(wú)關(guān)。因此,我們可以在特定時(shí)刻凍結(jié)旋轉(zhuǎn)矢量。
從電壓和電流量中去除時(shí)間依賴(lài)性,使我們能夠?qū)⑺鼈儽硎緸閺?fù)值、時(shí)間無(wú)關(guān)的數(shù)字。這大大簡(jiǎn)化了電路分析。一旦我們計(jì)算了電壓或電流量的矢量,我們就可以重新引入旋轉(zhuǎn)方面來(lái)確定該量的實(shí)際時(shí)域表達(dá)式。
簡(jiǎn)而言之,相量消除了時(shí)間依賴(lài)性的復(fù)雜性,使描述電壓和電流量變得更加容易。粗略地說(shuō),您可以將相量視為單頻正弦波的低通或直流等效物。
推導(dǎo)調(diào)制帶通信號(hào)的低通等效值
到目前為止,我們假設(shè)正弦波具有固定的振幅和相位。然而,類(lèi)似的分析可以應(yīng)用于具有緩慢變化的幅度和相位的固定頻率fc的正弦波。設(shè)以?c為中心的調(diào)制波定義為:
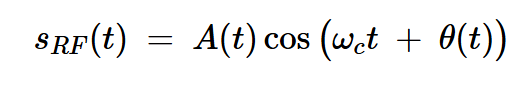
方程式5
其中A(t)和θ(t)是時(shí)變信號(hào)的瞬時(shí)振幅和相位。上述方程式可以改寫(xiě)為:
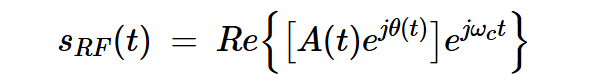
方程式6
方程式7將括號(hào)內(nèi)的項(xiàng)分開(kāi):
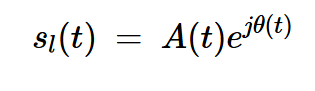
方程式7
該術(shù)語(yǔ)是帶通信號(hào)的復(fù)基帶表示。上述方程也可以笛卡爾形式表示:
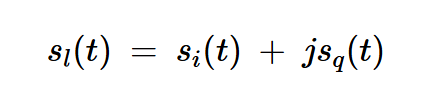
方程式8
其中si(t)和sq(t)是等效基帶信號(hào)sl(t)的實(shí)值同相和正交分量。這些組件由下式給出:
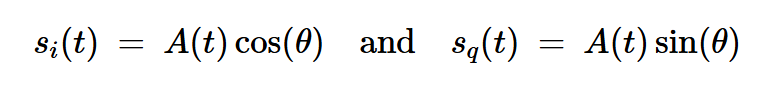
方程式9
因?yàn)閹ㄐ盘?hào)的同相和正交分量變化緩慢,所以我們知道它們都是低通信號(hào)。將sl(t)的笛卡爾形式代入方程6,我們可以用同相和正交分量來(lái)表示原始RF波:
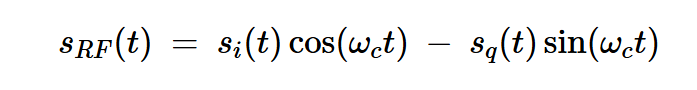
方程式10
上述方程表明,帶通信號(hào)可以用兩個(gè)低通信號(hào)來(lái)表示,特別是其同相和正交分量。
等效低通信號(hào)的可視化表示
帶通信號(hào)的復(fù)低通表示可以被視為時(shí)變相量,其起點(diǎn)位于(sI-sQ)復(fù)平面的原點(diǎn)。如圖5所示。
等效基帶信號(hào)sl(t)表示為(sI-sQ)平面中的時(shí)變相量
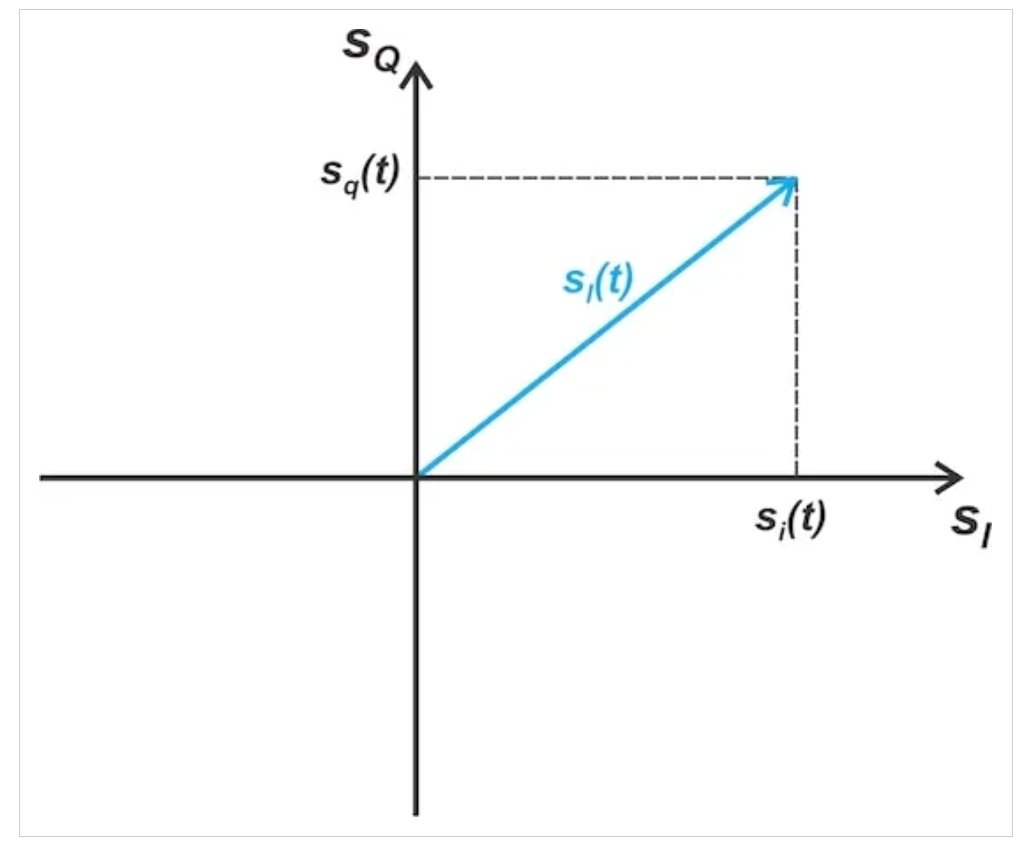
圖5等效基帶信號(hào)sl(t)表示為(sI-sQ)平面中的時(shí)變相量
由于同相和正交分量(分別為si(t)和sq(t))是時(shí)間的函數(shù),相量矢量的末端在(si-sq)平面內(nèi)移動(dòng)。
從方程6中,我們觀察到等效基帶信號(hào)sl(t)乘以復(fù)指數(shù)exp(jωct),得到帶通信號(hào)sRF(t)。因此,向量sl(t)和(sI-sQ)平面以角速度?c=2πfc旋轉(zhuǎn)。
包括旋轉(zhuǎn)方面的復(fù)平面中的時(shí)變相量。
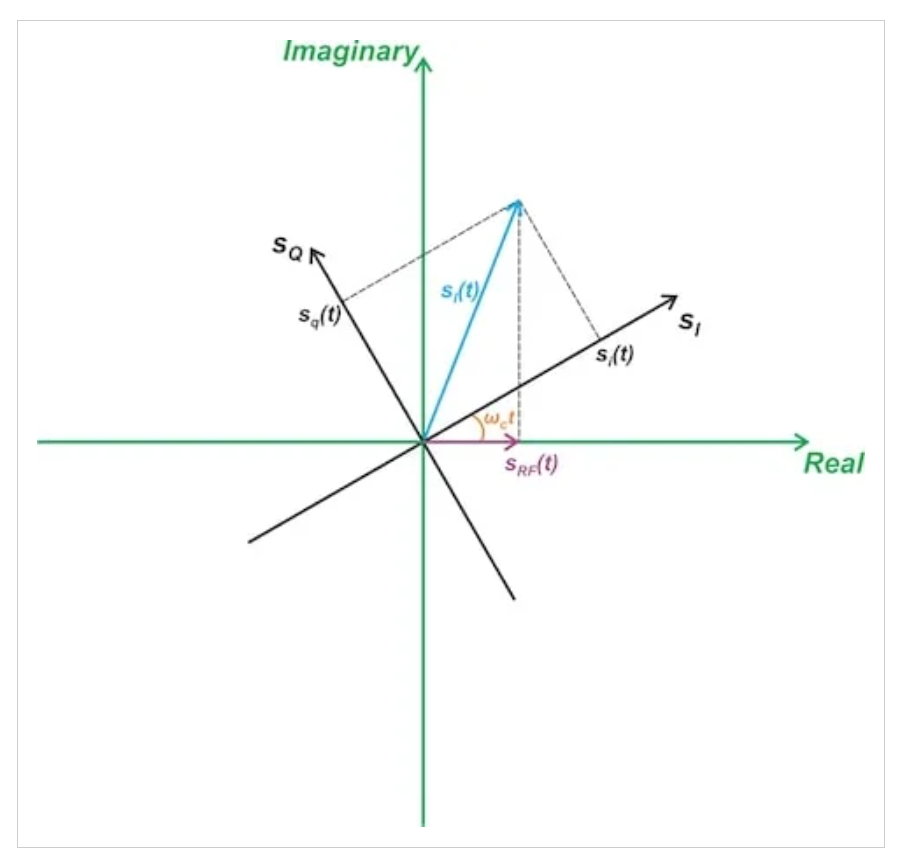
圖6包括旋轉(zhuǎn)方面的復(fù)平面中的時(shí)變相量
原始帶通信號(hào)sRF(t)是該時(shí)變相量在表示實(shí)軸的固定線上的投影。
重建帶通信號(hào)
方程10立即告訴我們?nèi)绾螐耐嗪驼环至恐貥?gòu)帶通信號(hào)。低通到通帶轉(zhuǎn)換的電路如圖7所示。
從低通同相和正交信號(hào)生成通帶信號(hào)的框圖。
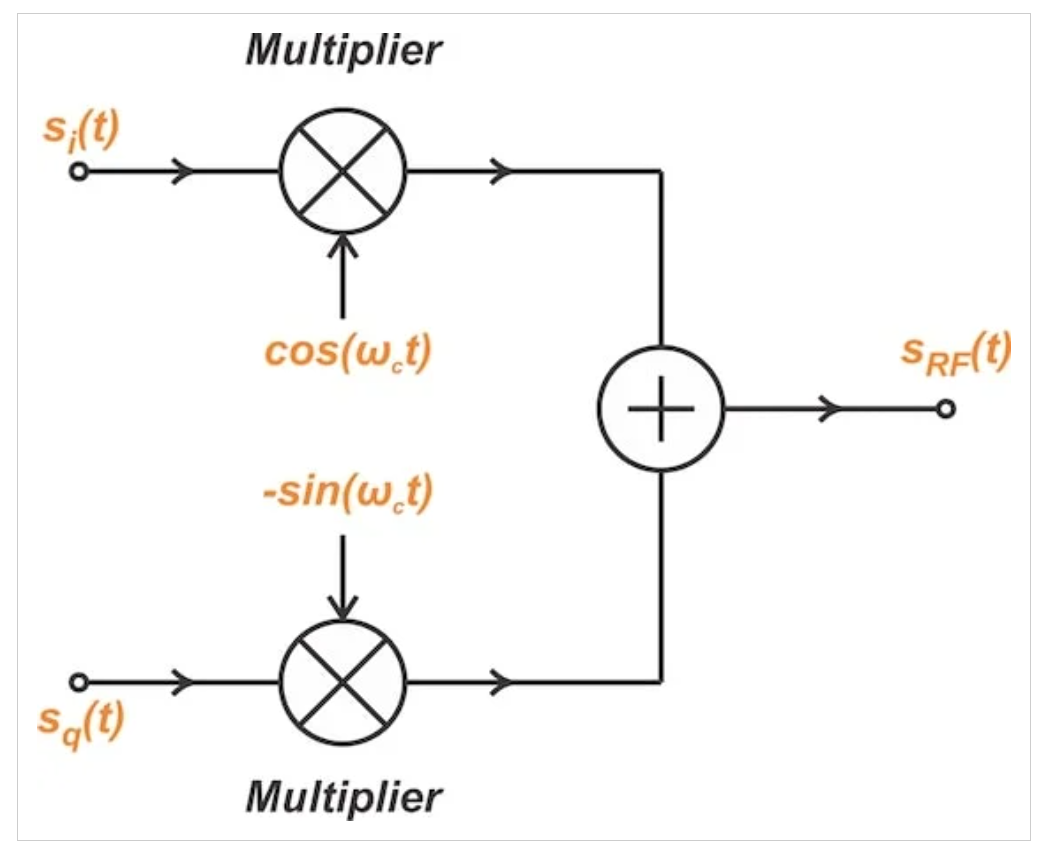
圖7從低通同相和正交信號(hào)生成帶通信號(hào)的框圖。
接下來(lái),我們需要從帶通信號(hào)中確定等效基帶信號(hào)。我們將從sRF(t)乘以2cos(?ct)開(kāi)始:
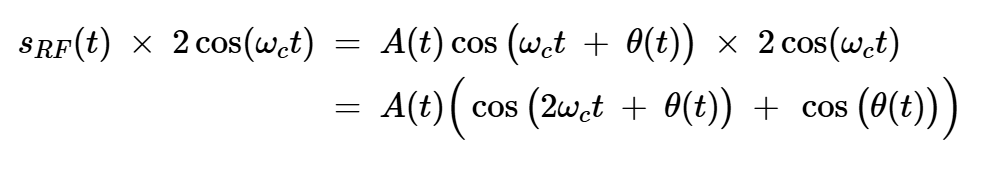
方程式11
如果我們以?xún)杀遁d波頻率對(duì)信號(hào)分量進(jìn)行濾波,我們得到:
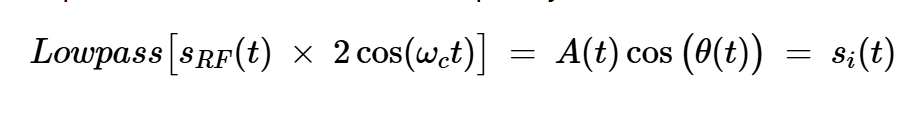
方程式12
同樣,將sRF(t)乘以-2sin(?ct)得到:
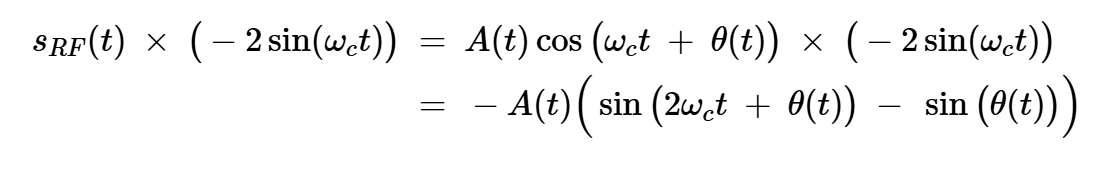
方程式13
應(yīng)用適當(dāng)?shù)牡屯V波器可以消除載波頻率兩倍的信號(hào)分量,從而:
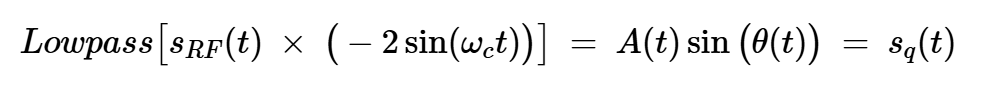
方程式14
圖8顯示了我們?nèi)绾问褂靡粚?duì)乘法器和一對(duì)低通濾波器來(lái)實(shí)現(xiàn)方程12和14。
用于從帶通信號(hào)生成低通同相和正交信號(hào)的框圖。
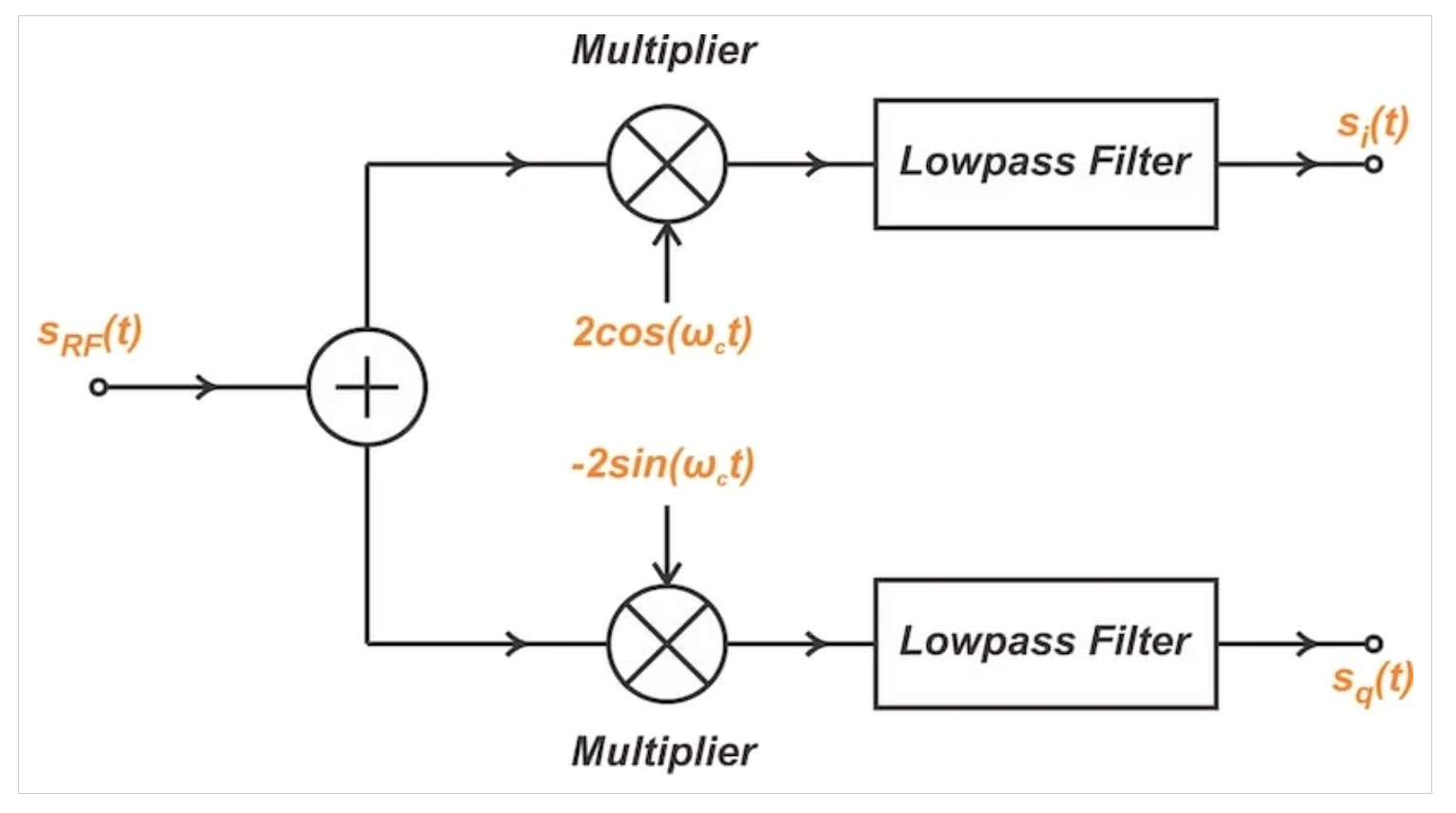
圖8用于從帶通信號(hào)生成低通同相和正交信號(hào)的框圖
總結(jié)
實(shí)值通帶信號(hào)中的所有信息都包含在相應(yīng)的復(fù)值基帶信號(hào)中。在本文中,我們學(xué)習(xí)了如何推導(dǎo)帶通信號(hào)的低通復(fù)等效值,反之亦然。
值得注意的是,擴(kuò)展此討論允許我們使用復(fù)數(shù)低通濾波器來(lái)表示帶通濾波器。為帶通信號(hào)和濾波器建立低通模型具有重大的實(shí)際意義。例如,現(xiàn)代通信收發(fā)器應(yīng)用這些模型對(duì)復(fù)雜的基帶信號(hào)進(jìn)行數(shù)字處理,從而減少了對(duì)通帶信號(hào)進(jìn)行模擬處理的需要。
圖7和圖8所示的電路對(duì)于理解線性調(diào)制方案至關(guān)重要,無(wú)論是模擬還是數(shù)字。在下一篇文章中,我們將看到Weaver調(diào)制器如何結(jié)合這些電路來(lái)生成單邊帶AM信號(hào)。



評(píng)論