相位差與相移

相位差用于描述兩個或多個交流量達到最大值或零值時在角度或弧度上的差異

相量(Phasor)是分析交流電路中各元件行為的有效工具，尤其適用于同頻電路。兩個相量相加的結果取決于它們的相對相位關系——由于相位差的存在，它們可能是"同相"或"異相"。

正弦波是一種沿時間軸水平呈現的交流量。作為時變量，正弦波在π/2時刻達到正最大值，在3π/2時刻達到負最大值，并在0、π和2π時刻通過零軸基準線。

但并非所有正弦波都會同時通過零軸點，相比另一個正弦波，它們可能向右或向左"偏移"一定量。例如比較電壓波形與電流波形時，就會在兩個正弦波之間產生角度偏移或相位差。任何在t=0時不經過零點的正弦波都存在相移。

正弦波的相位差(又稱相移)是指波形沿水平零軸相對于某參考點偏移的角度Φ(希臘字母Phi)，單位可為度或弧度。換言之，相移是多個波形沿共同軸的橫向差異，同頻率正弦波之間可能存在相位差。

交流波的相位差Φ在一個完整周期內可在0到最大周期T之間變化，對應水平軸上Φ=0到2π(弧度)或Φ=0到360°的范圍(取決于角度單位)。

相位差也可用時間偏移τ表示(單位為秒)，例如+10ms或-50μs，代表周期T的分數。但通常更習慣用角度值表示相位差。

因此，先前建立的正弦電壓/電流瞬時值方程需加入相位角修正，新通用表達式為：

相位差方程

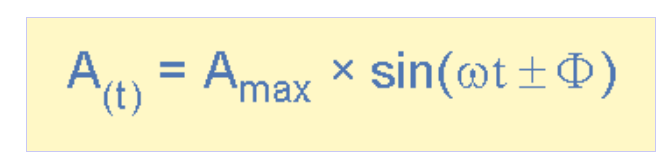
(此處插入相位角公式圖)

其中：

Am-波形振幅

ωt-角頻率(弧度/秒)

Φ-相位角(度或弧度)，表示波形相對于參考點的左右偏移

若正弦波的正斜率在t=0"之前"穿過水平軸，則波形左移(Φ>0)，相位角為正(+Φ)，形成超前相位角。這意味著波形比0°基準更早出現，對應相量逆時針旋轉。

反之，若正斜率在t=0"之后"穿過水平軸，則波形右移(Φ<0)，相位角為負(-Φ)，形成滯后相位角。這意味著波形比0°基準更晚出現，對應相量順時針旋轉。兩種情況如下圖所示：

正弦波的相位關系

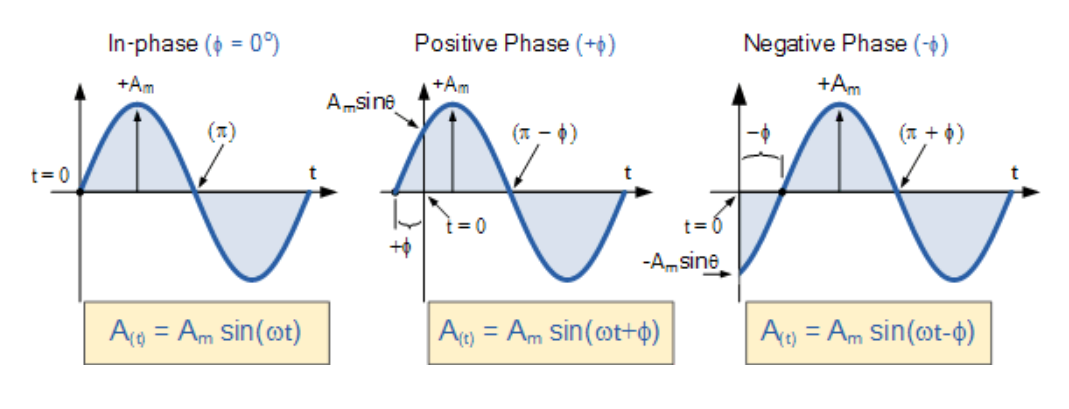
(此處插入正弦波相位關系圖)

首先假設兩個交流量(電壓v和電流i)具有相同頻率?(Hz)。由于頻率相同，角速度ω也必然相同。因此在任意時刻，電壓v與電流i的相位相同。

在特定時間段內，旋轉角度始終相同，故v與i的相位差為零(Φ=0)。由于電壓v和電流i頻率相同，它們會在同一時間達到正最大值、負最大值和零值(盡管幅值可能不同)。此時稱這兩個交流量"同相"。

兩個同相正弦波

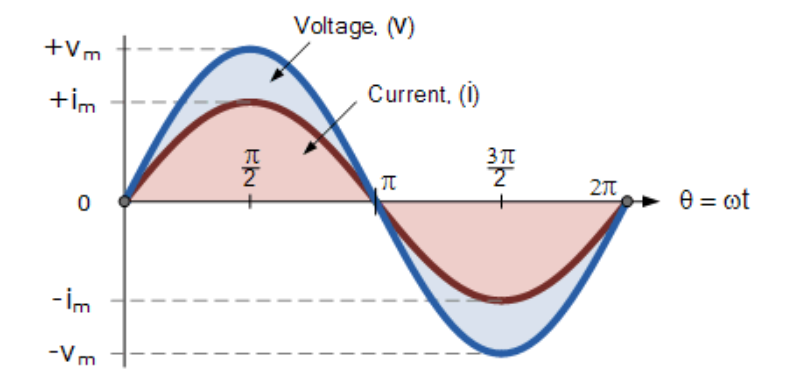
(此處插入同相正弦波圖)

現假設電壓v與電流i之間存在30°相位差(Φ=30°或π/6弧度)。由于兩者旋轉速度相同(即頻率相同)，該相位差在所有時刻保持恒定。如下圖所示，兩波形間30°的相位差用Φ表示：

正弦波的相位差

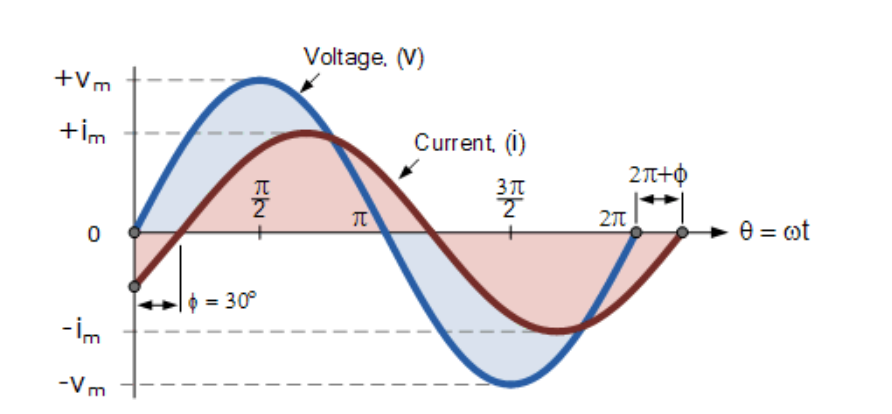
(此處插入兩正弦波相位差圖)

上方電壓波形從水平參考軸零點開始，但同一時刻電流波形仍為負值，直到30°后才穿過參考軸。因此當電流波形穿過參考軸達到峰值和零值時，總比電壓波形延遲，兩者存在相位差。

由于兩波形不再"同相"，而是存在Φ(本例為30°)的"異相"。可以說兩波形現在有30°相位差。也可表述為電流波形比電壓波形"滯后"相位角Φ。因此上例中的相位關系表達式為：

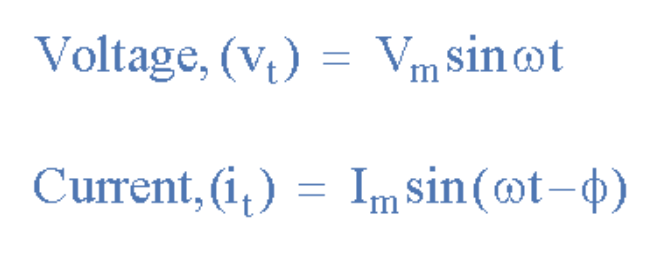
(此處插入滯后相位差公式圖)

其中電流i滯后電壓v相位角Φ

同理，若電流i先于電壓v穿過參考軸達到峰值和零值，則稱電流"超前"電壓一定相位角。此時兩波形存在超前相位差，表達式為：

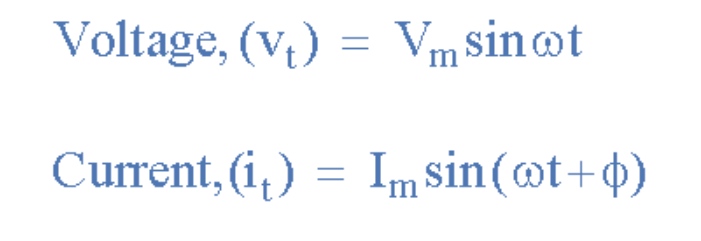
(此處插入超前相位差公式圖)

其中電流i超前電壓v相位角Φ

通過"超前"和"滯后"術語，可以描述同頻率正弦波在相同參考軸上的相位關系。上例中兩波形相位差30°，既可說i滯后v，也可說v超前i——取決于選擇哪個作為參考。

兩波形間的相位關系可通過測量它們沿水平零軸穿過時具有"相同斜率方向"(正或負)的位置來確定。在交流功率電路中，這種描述同一電路內電壓與電流正弦波關系的能力至關重要，構成了交流電路分析的基礎。

余弦波形

至此我們明白：當波形相對于另一正弦波向右或左"偏移"時，表達式變為Amsin(ωt±Φ)。但若某波形在參考波形之前90°(π/2弧度)以正斜率穿過零軸，則稱為余弦波，其表達式為：

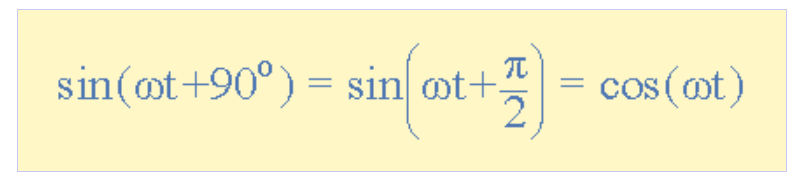
(此處插入余弦表達式圖)

余弦波(簡稱"cos")在電氣工程中與正弦波同等重要。余弦波與正弦波具有相同形狀(均為正弦函數)，但超前了+90°(即1/4周期)。

正弦波與余弦波的區別

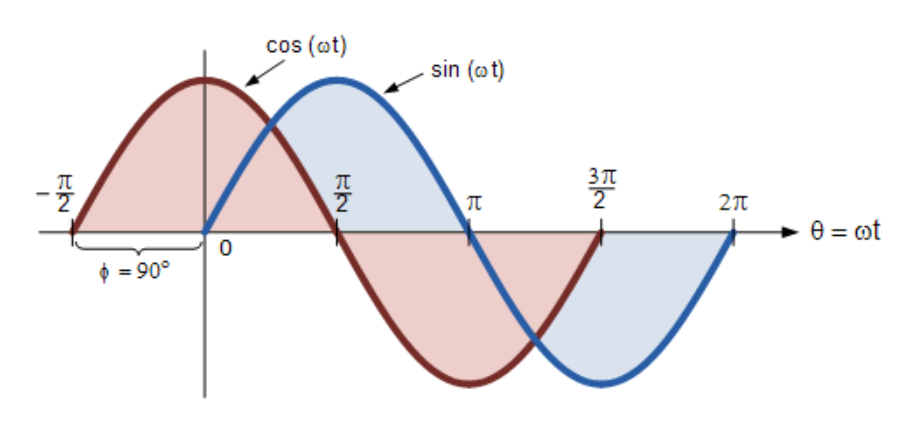
(此處插入相位差對比圖)

也可認為正弦波是向另一方向偏移-90°的余弦波。無論哪種情況，處理含角度的正弦波或余弦波時，以下規則始終適用：

正弦波與余弦波的關系

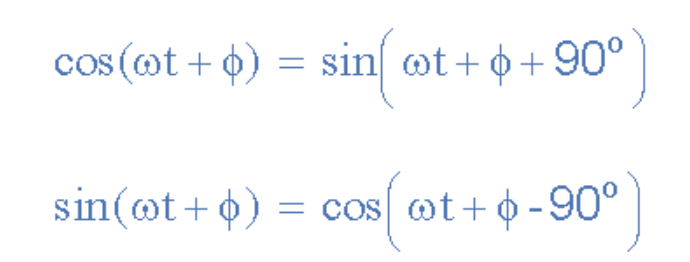
(此處插入正弦余弦關系圖)

比較兩個正弦波時，通常將其關系表示為具有正幅值的正弦或余弦函數，這可通過以下數學恒等式實現：

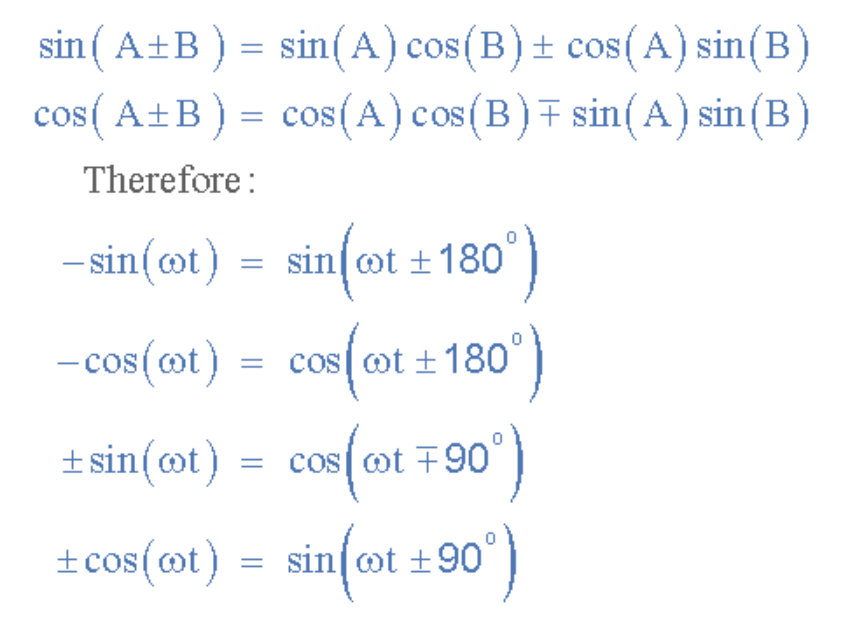
(此處插入正弦余弦恒等式圖)

利用這些關系式，我們可以將任意含角度差或相位差的正弦波形轉換為余弦波形，反之亦然。

在下一篇關于相量的教程中，我們將采用圖形化方法，通過單相交流量的相量表示及相量代數運算，來直觀比較兩個正弦波的相位差。