NF測量的Y因子法的增益定義：可用增益還是插入增益？

Y因子法是一種廣泛用于測量射頻元件增益和噪聲系數（NF）的技術。本文將幫助您了解插入增益和可用增益之間的差異，同時避免測量噪聲系數時可能出現的重大誤差。

原則上，Y因子法是一種相對簡單的測量RF組件增益和噪聲系數（NF）的方法。然而，在實踐中需要仔細注意一些錯綜復雜的問題。一些非理想效應，如測試設備NF的不確定性以及與噪聲源本身相關的不確定性，可能會導致測量不確定性。另一個微妙之處是，該方法實際上測量和使用DUT（被測器件）插入增益，而不是其可用增益。

Y因子法簡介

噪聲系數測量的Y因子法包括兩個步驟：

圖1（a）所示的測量步驟，用于確定由Tcas表示的DUT接收器系統的噪聲溫度

圖1（b）的校準步驟，確定接收器TR接收器的噪聲溫度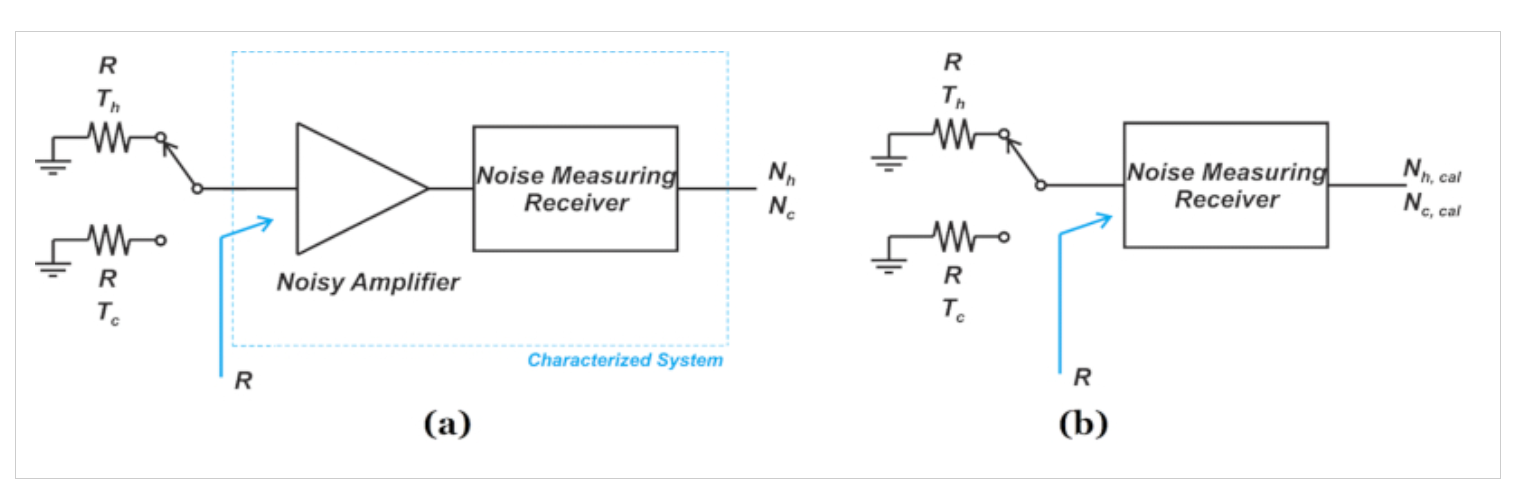

圖1 Y因子法測量噪聲系數的兩個步驟：（a）測量和（b）校準

在測量Tcas和TRecever之后，我們可以應用Friis方程來計算DUT的噪聲溫度：

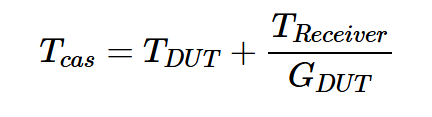
方程式1

其中TDUT和GDUT分別表示DUT的噪聲溫度和增益。從測量裝置獲得的噪聲功率（圖1（a）中的Nh和Nc）被DUT增益放大；然而，Nh、cal和Nc、cal沒有經歷這種增益（圖1（b））。因此，GDUT可以通過以下方程式進行估算：

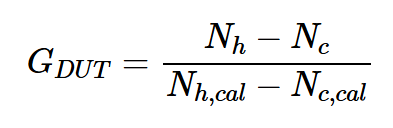
方程式2

可用功率增益

噪聲系數定義中使用的功率增益是可用功率增益GA，如下圖2所示。可用功率增益是雙端口網絡PAVN（圖2（a））可用功率與源PAVS可用功率的比值。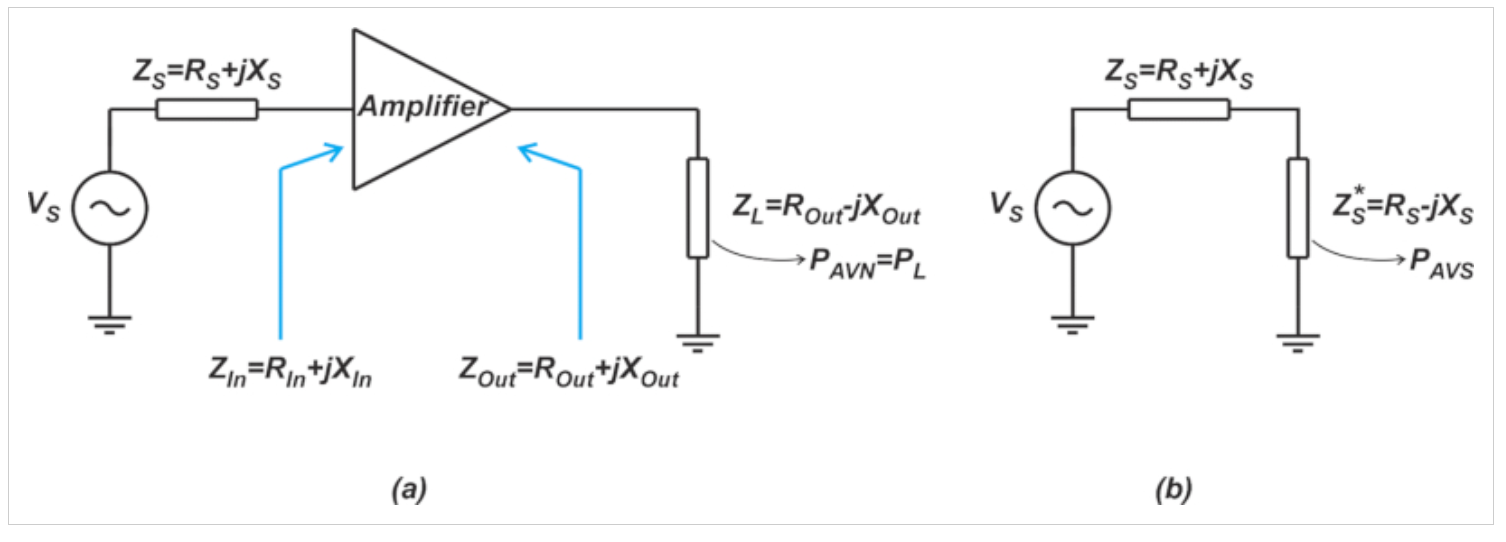  

圖2 可用功率增益定義

請注意，對于PAVN和PAVS測量，被測端口都連接到其共軛匹配的負載。例如，為了找到PAVN，模塊輸出連接到Zout=Rout+jXout的復共軛，即ZL=Rout-jXout。我們從方程1中獲得的功率不是可用的功率增益。為了將其與可用增益區分開來，它被賦予了一個特定的名稱：插入增益，這將在下面討論。

插入功率增益

圖3說明了插入功率增益的定義。

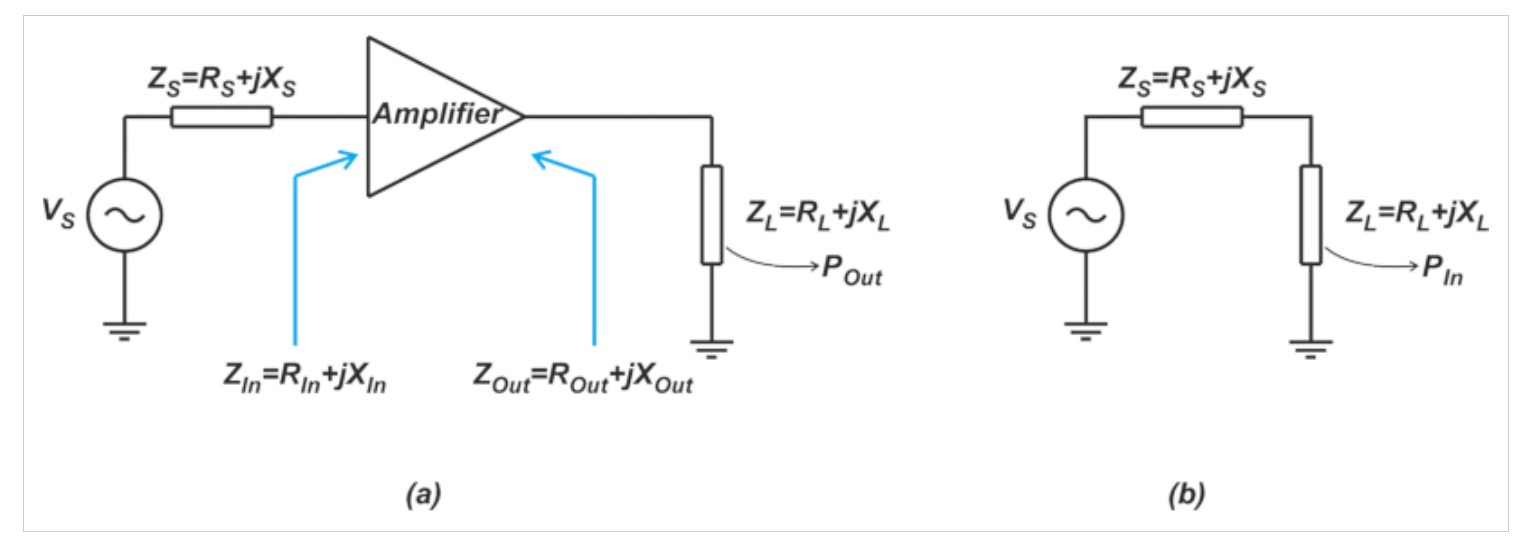
圖3 插入功率增益定義

插入功率增益取決于源阻抗和負載阻抗（ZS和ZL）。如圖3（a）所示，我們將DUT連接到ZL，同時其輸入由ZS的源阻抗驅動，并測量輸送到負載的功率（圖3中用POut表示）。我們還測量了源可以直接傳遞給ZL的功率，如圖3（b）中的PIn所示。POut與PIn的比率是DUT的插入增益。從這個解釋中可以清楚地看出，插入增益對應于我們在給定的ZS和ZL之間插入DUT時獲得的功率增益的變化。

使用插入增益引入的誤差

將Y因子法的測量和校準步驟（圖1（a）和（b））與插入增益定義（圖3（a））進行比較，我們觀察到，我們從方程2中獲得的增益實際上是插入增益，而不是可用增益。可以測量DUT的可用增益；然而，這需要兩次額外的功率測量，其中負載阻抗必須調諧到與被測端口共軛匹配。

然而，插入增益是從Y因子法所需的四個功率測量值中獲得的。我們實際上假設插入增益等于可用增益。如果不是這樣，我們的測量將引入誤差（方程式1）。可以看出，可用增益GA和插入增益Gi之間的差由下式給出：

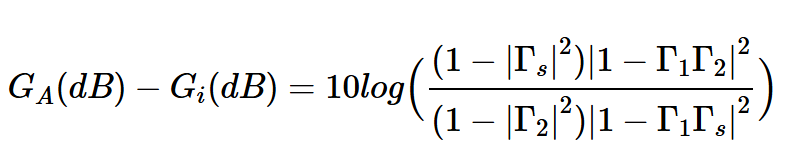
方程式3

其中Γ1是觀察噪聲測量接收器的反射系數；Γ2是觀察DUT輸出時觀察到的值；Γs是噪聲源的反射系數（圖4）。

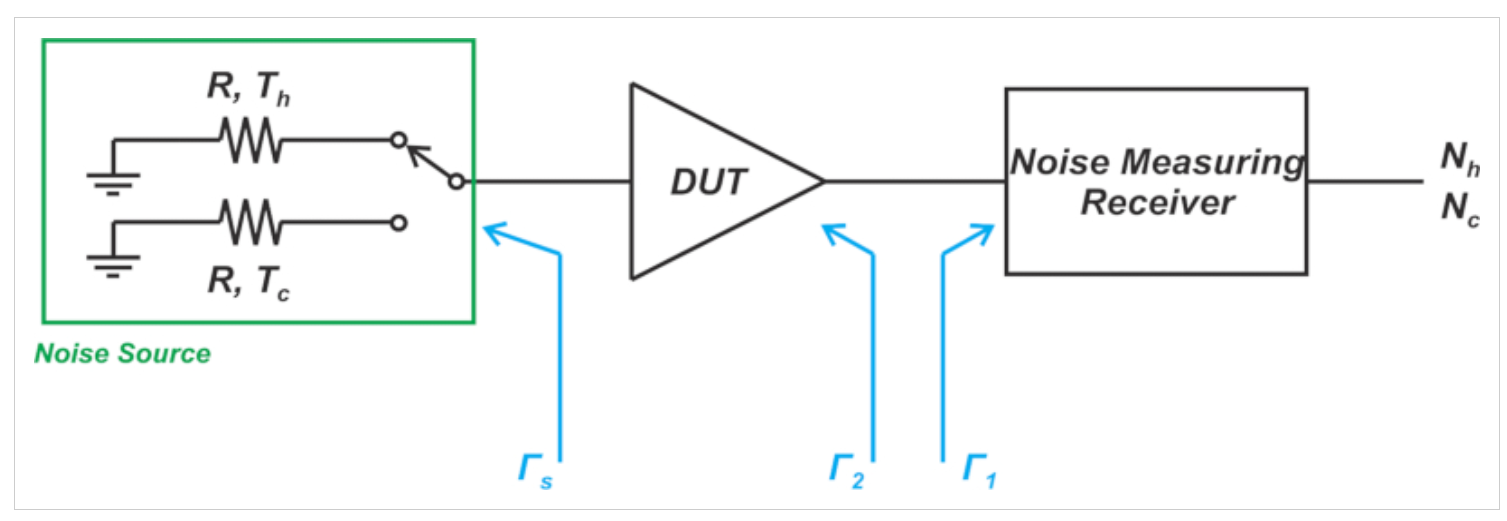
圖4 噪聲源、DUT輸出和噪聲測量接收器的反射系數

請注意，在完全匹配的情況下（Γ1=Γ2=Γs=0），插入增益等于可用增益。在上述方程中，需要了解反射系數的幅度和相位才能從Gi中找到GA。通常，相位信息不可用，我們只能找到誤差極限。圖5顯示了作為匹配水平函數的插入增益和可用增益之間的差異。

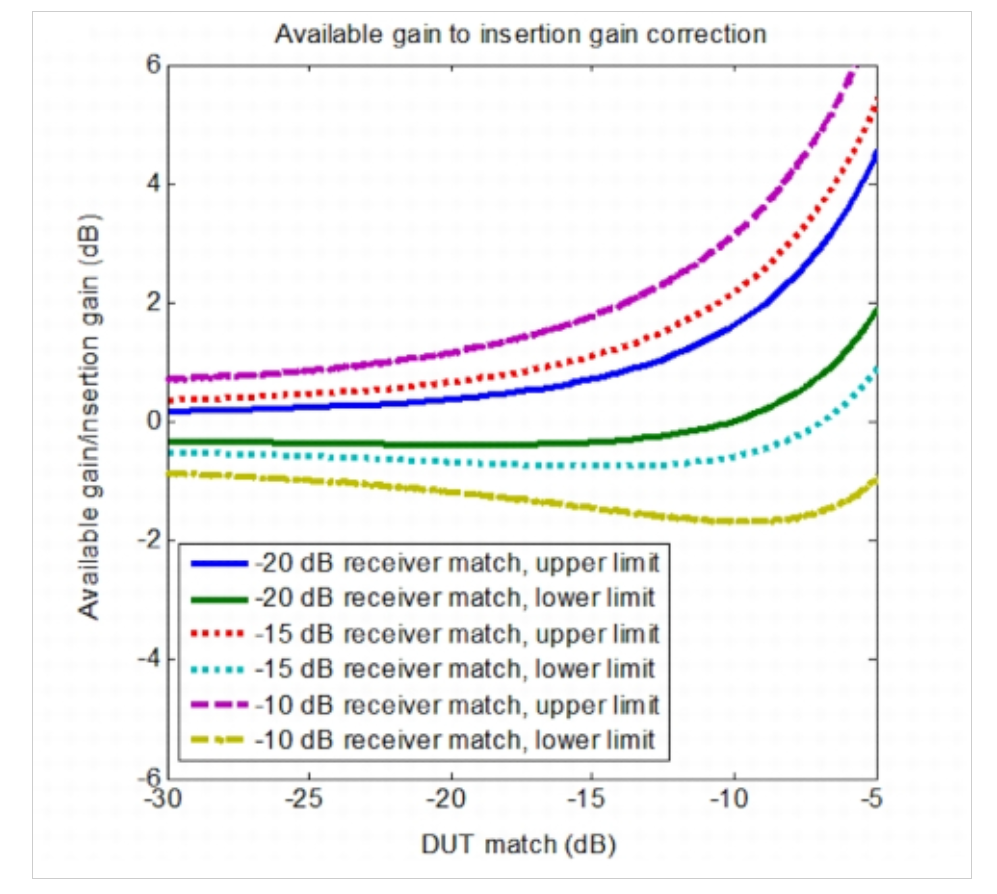
圖5可用增益與插入增益之比，作為接收器和DUT匹配的函數。圖片由安立提供

在上圖中，x軸是DUT輸入和輸出匹配（為簡單起見，假設DUT的輸入和輸出匹配對相同）。y軸是兩個功率增益之間的差值，單位為分貝。假設噪聲源匹配為-20 dB，并且假設DUT具有良好的隔離（|S21×S12|=0.1）。請注意，隨著DUT匹配度降低到-10dB以上，兩種增益之間的差異變得更加顯著。在這種情況下，增益誤差可能會在測量的NF值中引入顯著誤差。

S—增益誤差的參數校正

此時，您可能會想知道是否可以使用DUT的S參數以及方程3來從插入增益中獲得可用增益。通過將GA（而不是Gi）代入Friis方程，我們可以校正增益誤差。這似乎是有益的，但有兩點值得一提。

首先，請注意，我們通常沒有反射系數（Γ1、Γ2和Γs）的相位信息。對于標量測量，我們不知道矢量反射系數將如何組合以產生最終誤差。假設向量失配可用，我們可以從Gi中找到GA。

然而，還有另一個問題可能會妨礙我們進行更準確的測量：DUT和測量設備的噪聲系數是其驅動點阻抗的函數。圖5通過假設DUT的噪聲性能以圖形方式說明了這一點。

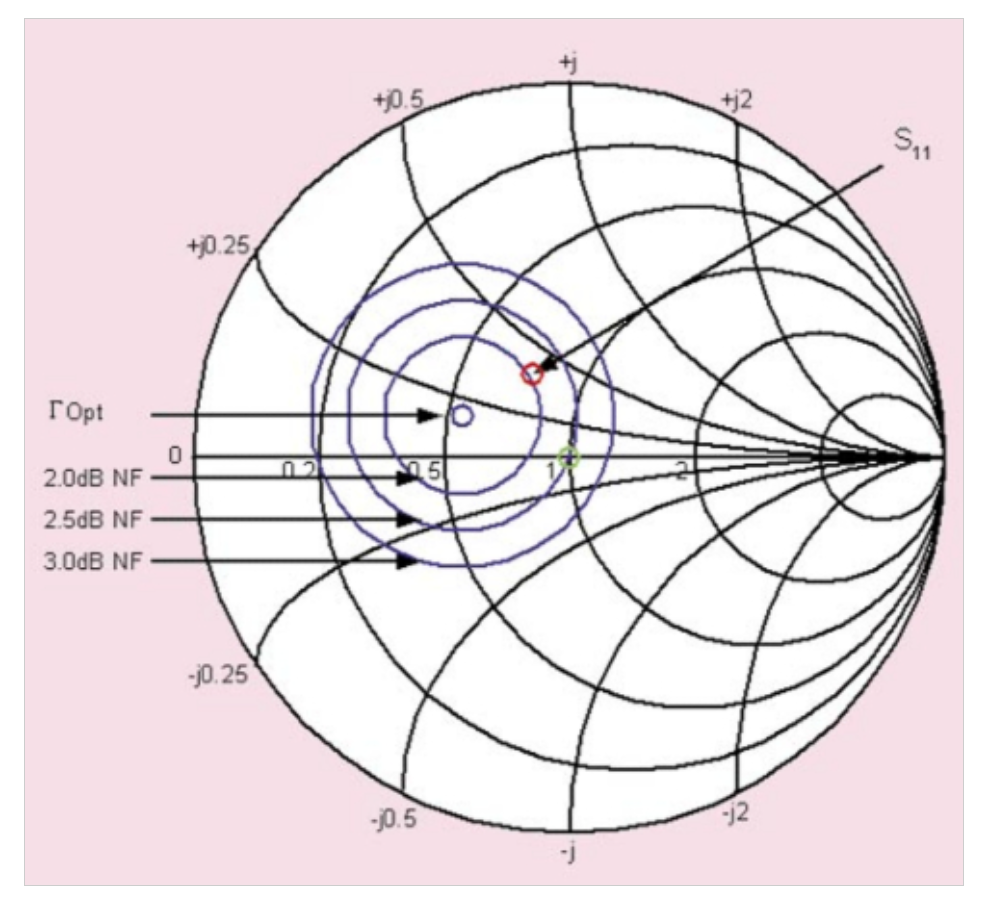
圖6史密斯圓圖展示了驅動點阻抗對噪聲系數的影響。圖片由D.Boyd提供

當DUT由50Ω的源阻抗（對應于史密斯圓圖中心的綠色圓圈）驅動時，其噪聲系數為2.5 dB。然而，當源阻抗等于DUT S11的復共軛（圖中紅色圓圈標記）時，噪聲系數為2 dB。S參數不能為我們提供有關設備噪聲性能的任何信息。因此，雖然S參數校正可用于從Gi中找到GA，但它不允許我們考慮DUT NF的變化。如果不了解NF隨源電阻的變化，S參數校正甚至會增加NF測量誤差。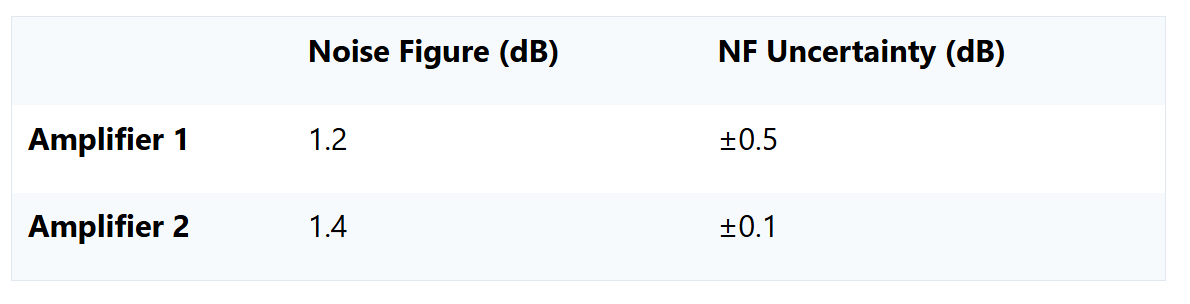 

確定NF對源阻抗的依賴性需要專門的NF測量設備，該設備使用短截線調諧器向設備施加一系列復阻抗。然后對這些測量值進行分析，以在史密斯圓圖上產生與圖5所示類似的NF圓形輪廓。應該指出的是，常見的噪聲系數分析儀和網絡分析儀無法產生這些NF輪廓。

明確測量不確定度的必要性

沒有噪聲輪廓，對噪聲系數測量應用失配校正是無效的。在這些情況下，建議盡可能減少不同端口的阻抗失配，然后將殘余失配視為測量不確定度。除了失配效應外，完整的不確定性分析還可以解釋其他非理想效應，例如測試設備NF的不確定性以及與噪聲源本身相關的不確定性。不確定度分析是每種測量的關鍵，包括NF測量。下表強調了通過比較兩個不同的假設放大器來了解測量不確定度的重要性。

在不考慮不確定性的情況下，人們立即選擇放大器1作為性能更高的設備。然而，考慮到測量的不確定性，我們觀察到放大器1的噪聲系數可能高達1.7 dB，而放大器2的最大NF為1.5 dB。在進行噪聲系數測量時，需要注意的一個關鍵參數是測量不確定性。在未來的文章中，我們將研究Y因子法的測量不確定度。

Y因子方法綜述

Y因子法實際測量和使用DUT的插入增益，而不是其可用增益。在存在阻抗失配的情況下，這可能會導致顯著的誤差。由于插入增益的測量比可用增益容易得多，我們通常假設這兩個功率量相等。然而，為了限制誤差，應盡量減少不同端口的阻抗失配。殘余失配誤差通常被視為測量不確定度。