基于LabVIEW仿真的全局最短路徑的遺傳算法設(shè)計(jì)
最短路徑問題是圖論研究中的一個(gè)經(jīng)典算法問題,旨在尋找圖(由結(jié)點(diǎn)和路徑組成的)中結(jié)點(diǎn)之間的最短路徑。問題的主要種類有:確定起點(diǎn)的最短路徑問題;確定終點(diǎn)的最短路徑問題;確定起點(diǎn)終點(diǎn)的最短路徑問題;全局最短路徑問題。其中全局最短路徑是求連接圖中所有點(diǎn)的最短路徑,它的限制最少,答案的可能性卻最多。同時(shí)當(dāng)加入一定的限制條件后也可以相應(yīng)的轉(zhuǎn)化成前3種問題,所以更值得研究推廣。
現(xiàn)有的解決最短路徑問題的遺傳算法大多是將圖轉(zhuǎn)化成一棵樹,通過各種遍歷手段,得到與這棵樹唯一對(duì)應(yīng)的一個(gè)數(shù)組排列(或向量),并以此作為遺傳算法的種群個(gè)體。生成樹以及遍歷方法的優(yōu)劣就決定了該種遺傳算法的好壞。本文并不是提出一種改進(jìn)的生成樹或遍歷的方法,相反,完全隨機(jī)生成樹,不做任何限制,也未對(duì)樹進(jìn)行遍歷,只是在遺傳算法對(duì)每代種群進(jìn)行優(yōu)勝劣汰時(shí),同時(shí)對(duì)不合格的個(gè)體進(jìn)行淘汰。省略了生成樹以及遍歷的過程,也就相當(dāng)于化簡(jiǎn)了編碼解碼過程。
1 問題描述
在一定區(qū)域內(nèi)分布著一些點(diǎn),要使用線段將所有點(diǎn)連接到同一個(gè)網(wǎng)絡(luò)下。如何連接這些點(diǎn)才能令使用到的所有線段的總長(zhǎng)度最短。建立相應(yīng)的數(shù)學(xué)模型。設(shè)有M個(gè)點(diǎn),坐標(biāo)記為Pi(xi,yi),1≤i≤M則每?jī)蓚€(gè)點(diǎn)之間的距離為
![]()
要連接M個(gè)點(diǎn)并使總距離最短,則至少要有M-1條線段,那么目標(biāo)函數(shù)即總距離
![]()
2 編碼
遺傳算法的編碼很重要,因?yàn)樵谡麄€(gè)過程中會(huì)不斷地對(duì)基因做交叉變異以及適應(yīng)度的運(yùn)算,所以編碼方式直接影響算法的速度。很明顯,編碼后的基因鏈越短,每個(gè)基因位上的基因種類越少,算法的運(yùn)行速度越快。使用二進(jìn)制編碼的話,雖然每個(gè)基因位上的基因種類只有2種,但如果點(diǎn)的個(gè)數(shù)較多,將會(huì)使基因鏈過長(zhǎng),在遺傳變異的過程中中間節(jié)點(diǎn)情況太多,使整個(gè)過程變得過于復(fù)雜,所以這里選擇用十進(jìn)制編碼的方法。
一般的編碼方法都是將節(jié)點(diǎn)和線段編號(hào),再通過某種運(yùn)算對(duì)用這些編號(hào)構(gòu)成的向量進(jìn)行一系列處理,得到較原向量更為簡(jiǎn)單或與連接方法能一一對(duì)應(yīng)的新向量,并以此作為種群個(gè)體。本文的方法中,線段不但有編號(hào),而且具有方向性。利用其方向性線段編號(hào)可以直接作為個(gè)體使用,省略了一般情況下的編碼解碼過程,所以運(yùn)算更加簡(jiǎn)單快捷。
2.1 個(gè)體確定
M個(gè)點(diǎn)兩兩相連,共有M(M-1)/2條線段,將所有線段編號(hào)。編號(hào)的順序規(guī)則為:
1)從1號(hào)點(diǎn)出發(fā),按順序依次連接2號(hào)點(diǎn)、3號(hào)點(diǎn)……M號(hào)點(diǎn)的線段,編號(hào)為1~M-1;
2)從2號(hào)點(diǎn)出發(fā),按順序依次連接3號(hào)點(diǎn)、4號(hào)點(diǎn)……M號(hào)點(diǎn)的線段,編號(hào)為M~2M-3;
3)直到M-1號(hào)點(diǎn)連接M號(hào)點(diǎn)的線段為最后一條線段。
每個(gè)基因就是1條線段,那么每個(gè)基因就有種可能,要使用數(shù)量最少的線段就連接所有點(diǎn),需要M-1條線段。如圖1所示網(wǎng)絡(luò),共有5個(gè)點(diǎn),兩兩相連共有l(wèi)O條線段,形成個(gè)體需要其中的4條線段,圖l所示的2個(gè)個(gè)體對(duì)應(yīng)的基因鏈即種群個(gè)體分別為{1、3、4、5}和{1、2、5、10}。
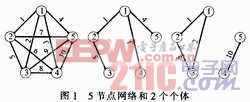
2.2 合法性判斷
很明顯不是任意4條線(以圖l的5個(gè)點(diǎn)為例)都適合作為初始種群的個(gè)體,所以在使用每個(gè)種群個(gè)體前判斷其合法性就相當(dāng)于減少了基因的種類,大大化簡(jiǎn)了運(yùn)算過程,免去一些不必要的計(jì)算,加快收斂速度。合法性可以通過以下3個(gè)條件進(jìn)行判斷:
條件1:不能出現(xiàn)重復(fù)編號(hào)。
如{1、1、2、3},其實(shí)只有3條線,這個(gè)個(gè)體必然是錯(cuò)誤的,在最開始就可以淘汰,不需要進(jìn)入循環(huán)中運(yùn)算。
條件2:4條線的編號(hào)必須從小到大。
如{1、2、3、5}和{5、3、1、2}是2種不同的種群個(gè)體,但實(shí)質(zhì)上是同樣的4條線,進(jìn)行了從小到大的定義后就可以避免產(chǎn)生大量的最優(yōu)解,導(dǎo)致運(yùn)算混亂。
條件3:必須保證所有點(diǎn)連在一起(或者沒有回路)。
如{1、2、5、10}(圖l第2個(gè)個(gè)體),連接了所有點(diǎn),但1、2、5構(gòu)成回路導(dǎo)致5個(gè)點(diǎn)被分成了兩部分,相當(dāng)于有一部分沒有被連接進(jìn)網(wǎng)絡(luò),此個(gè)體也要直接淘汰。
為了判斷上述3個(gè)條件是否滿足,需要建立2個(gè)數(shù)組,點(diǎn)信息數(shù)組Point[]和線信息數(shù)組Line[]。Point[]是二維數(shù)值數(shù)組,按點(diǎn)的編號(hào)順序存儲(chǔ),每一行存有一個(gè)點(diǎn)的橫縱坐標(biāo)2個(gè)數(shù)。Line[]是二維數(shù)值數(shù)組,按線段的編號(hào)順序存儲(chǔ),每一行存有一條線段信息,包括線段的端點(diǎn)和長(zhǎng)度3個(gè)數(shù)。圖2為5節(jié)點(diǎn)時(shí)LabVIEW前面板的模擬圖及2個(gè)數(shù)組的存儲(chǔ)情況。
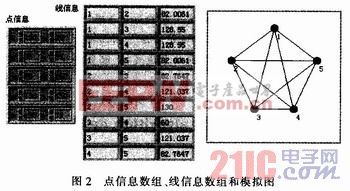
條件2易滿足,為滿足條件1和條件3,定義(M-1)xM階判斷矩陣A,表示被選中的線段與各節(jié)點(diǎn)的關(guān)系。每一行對(duì)應(yīng)一條線段,每一列依次對(duì)應(yīng)M個(gè)節(jié)點(diǎn)。在定義Line[]的2個(gè)端點(diǎn)時(shí),都是序號(hào)小的節(jié)點(diǎn)在前,大的在后,所以不妨把每條線段看成有方向的矢量,從小號(hào)節(jié)點(diǎn)指向大號(hào)節(jié)點(diǎn)。在矩陣對(duì)應(yīng)的位置,起點(diǎn)為-1,終點(diǎn)為1,其他點(diǎn)為O。以圖1為例,2個(gè)個(gè)體對(duì)應(yīng)的判斷矩陣分別為A1、3、4、5和A1、2、5、10。








評(píng)論