計算電磁學在電磁兼容仿真中的應用
加入技術交流群
1．2 矩量法
自從20世紀60年代Harrington提出矩量法基本概念以來，它在理論上日臻完善，并廣泛用于工程之中，特別是在電磁兼容領域，矩量法更顯示出其獨特的優越性。它的思想是將待求的積分或微分問題轉化為一個矩陣方程問題，借助于計算機，求得其數解。很多電磁場問題都歸結為這樣一個算子方程：
式中：L為算子；g為已知激勵函數；f為未知響應函數。展開未知函數f為有限個線性無關的已知簡單函數fn之和：
式中：an是展開系數；f1，f2，…，fn為展開函數或基函數。將式(8)代入式(7)，再應用算子L的線性，可以得到：
選一組線性無關的函數ωm(m=1，2，…，N)，分別與式(9)兩邊作內積。
因為m=1，2，…，N，所以得到N個方程，解出f。
矩量法就是這樣一種將算子方程轉化為矩陣方程的一種離散方法。
矩量法更適合于求解具有表面電流分布的各種幾何體，如計算天線遠、近場輻射場強、方向圖等。它的算法簡單，不需要設置邊界條件，而且對于適當的尺寸，求解速度較快。
1．3 時域有限差分法
K．S．Yee于1966年提出求解電磁問題的時域有限差分法，其原理非常簡單，即直接將時域Maxwell方程組的兩個旋度方程中關于空間變量和時間變量的偏導數用差商近似，從而轉換為離散網絡節點上的時域有限差分方程。
為了建立差分方程，首先要將求解空間離散化。通常是以一定形式的網格來劃分求解空間，Yee提出了如圖1所示的差分網格單元，其特點是在同一網格中，E和H的各分量在空間取值點交叉放置，使每個坐標面上的
的四周由
分量環繞，同時每個場四周由場環繞。這樣，配置符合Maxwell方程的基本要求，也符合電磁波空間的傳播規律，使電磁波的時域特性被直接反映出來，直接給出非常豐富的電磁場問題的時域信息。本文引用地址：http://www.104case.com/article/202428.htm
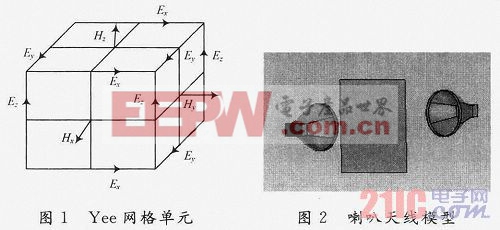
時域有限差分法在天線輻射特性計算、微波電路分析、散射體雷達散射截面等方面有廣泛的應用，對于計算孔縫對屏蔽效能的影響具有優越性。
評論