使用串聯和并聯RC和RL電路設計L形匹配網絡

通過RC和RL電路的品質因子（Q因子）以及這些電路的串并聯轉換，了解L形阻抗匹配方程

在本系列的前一篇文章中，我們學習了如何使用史密斯圓圖設計無源阻抗匹配網絡。除了使用這種圖形方法，還可以遵循分析方法并使用一些方程來獲得所需的匹配網絡。

首先，在深入阻抗匹配方程之前，我們需要了解兩個基本概念：RC和RL電路的品質因子以及這些電路的串并聯轉換。

RC和RL電路的品質因子定義

用Q表示的術語品質因子可以用多種方式定義。當談論儲能裝置（即電容器或電感器）時，Q表示我們的儲能裝置有多接近理想。例如，理想的電容器不會耗散任何能量，應該有無限的Q。現在，考慮一個模擬為并聯RC電路的真實電容器（圖1（a））。

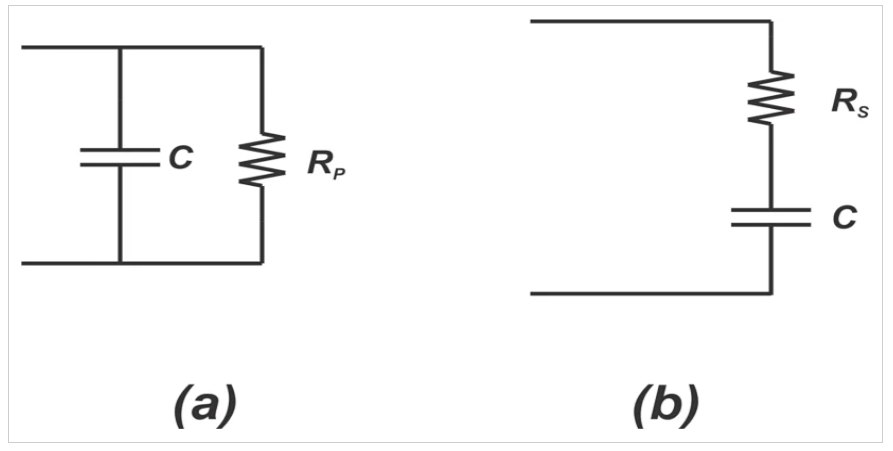
圖1 并聯RC電路（A）和串聯RC電路（b）

在這種情況下，電阻器可以表示實際電容器的電阻損耗。對于并聯RC電路，Q可以定義為：

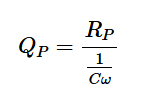
方程式1

接下來，讓我們看看這個方程式是否有意義。在圖1（a）的電路圖中，當RP變為無窮大時，我們只剩下一個理想的電容器（Q=∞）。這與上述方程一致，該方程在無限RP的極限下產生無限Q。

現在考慮一個帶有串聯電阻器RS的電容器，如圖1（b）所示。在這種情況下，Q被定義為：

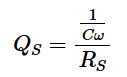
方程式2

在串聯RC電路中，當RS=0時，獲得了理想的儲能裝置。這也與方程2一致，方程2在RS=0的極限下產生無限Q。在方程式1中，Q被定義為不期望阻抗（RP）與電容性組件阻抗的比率，而方程式2將Q定義為電容性組件的阻抗與耗散性組件的電阻的比率。根據你的直覺，你認為并行RL（圖2（a））和串行RL（圖2中（b））的品質因子是如何定義的？

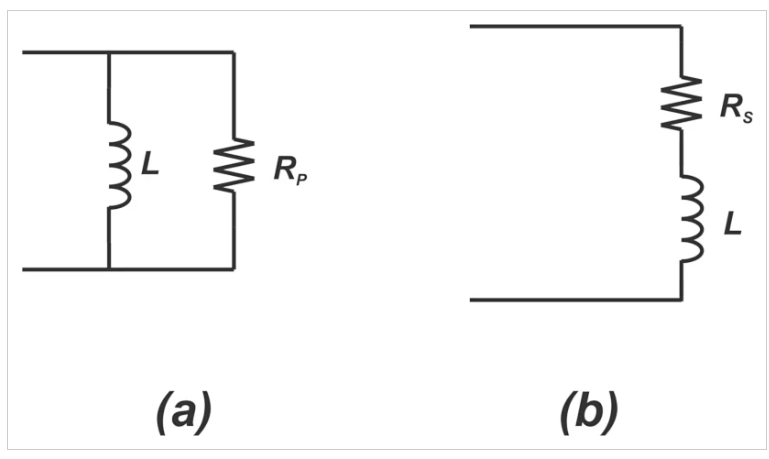
圖2 并聯RL電路（a）和串聯RL電路（b）

并聯RL電路（QP）和串聯RL電路（QS）的品質因子分別如方程式3和4所示：

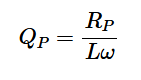
方程式3

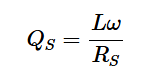
方程式4

再次注意，當RP趨于無窮大時，方程3產生無窮大的Q；隨著RS變為0，QS趨于無窮大。記住這些極端情況，您可以很容易地記住每種配置的正確方程。

RL和RC電路串并聯轉換

設計阻抗匹配網絡的一個關鍵步驟是將組件的串聯連接轉換為等效的并聯連接，反之亦然。在射頻文獻中，這通常被稱為串并聯轉換或并聯串聯轉換。例如，參考下圖3（a）所示的串聯RL電路。

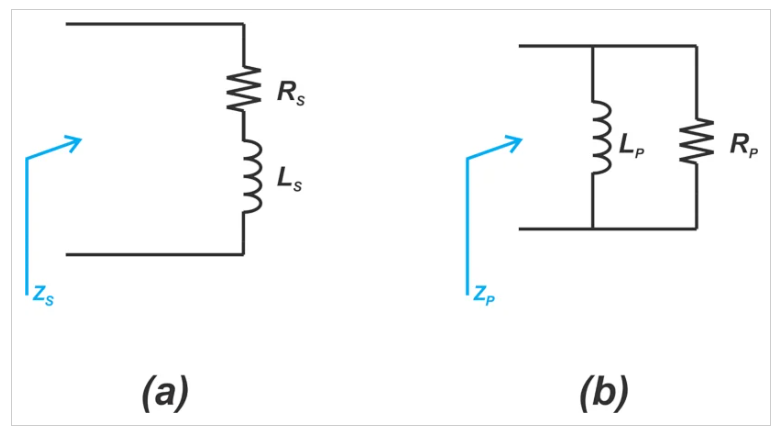
圖3 串聯RL電路（A）及其等效RL電路（b）

在單一頻率下，我們可以通過等效的并聯RL電路對串聯RL電路進行建模，如圖3（b）所示。通過將這兩個電路的輸入阻抗相等（ZS=ZP），我們可以根據串聯電路的分量值找到并聯電路的分量。這將產生以下方程組：

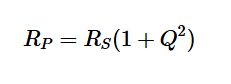
方程式5

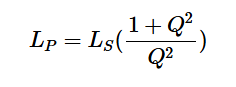
方程式6

其中Q表示電路的品質因子（上一節中的方程式3和4）。注意，串聯RL電路（QS）的Q和并聯等效電路（QP）的Q在兩個電路產生相同阻抗的頻率下是相同的。結果，等式5和6使用符號Q而不是QS或QP來表示品質因子。上述方程可用于將串聯電路轉換為并聯電路，反之亦然。同樣，我們可以推導出數學方程，將串聯RC電路（圖4（a））轉換為等效并聯電路（圖3（b）），反之亦然。

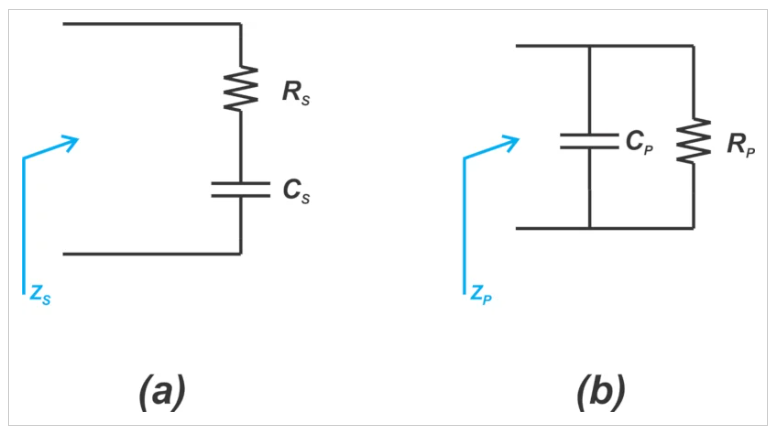
圖4 示例串聯RC電路（a）及其等效并聯電路（b）

方程式5也適用于RC電路的串并聯轉換。然而，請記住，現在Q項是RC電路的品質因子（方程式1和2）。電容值由以下方程式關聯：

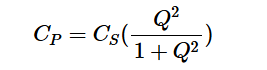
方程式7

上述方程式有簡單的解釋。方程式5顯示，并聯等效電阻比相應的串聯電阻大（1+Q2）倍。此外，假設Q相對較大，串聯和并聯電路的無功分量幾乎相同。讓我們看一個例子來澄清上述討論。

示例1：并聯和串聯RC電路的輸入阻抗

假設RF塊的輸入阻抗可以通過RP=50Ω和CP=3.88 pF的并聯RC電路進行建模，如下圖5所示。

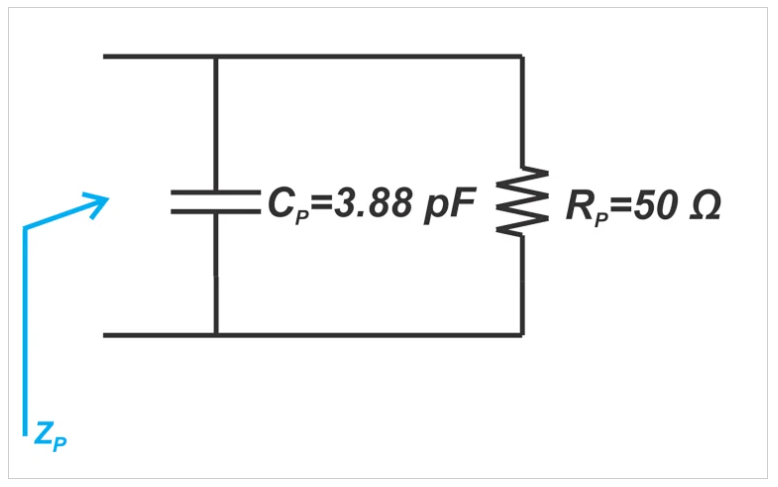
圖5 示例并聯RC電路RP=50Ω，CP=3.88 pF

找到1 GHz下的等效串聯RC電路。

通過應用方程式1，可以得出并聯RC電路的Q值：

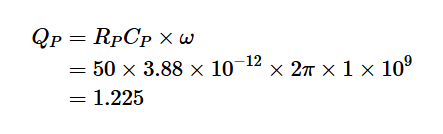
將Q=1.225代入方程式5和7，我們得到：

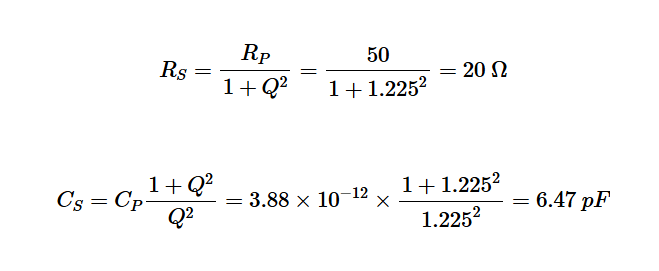
等效串聯電路如圖6所示。

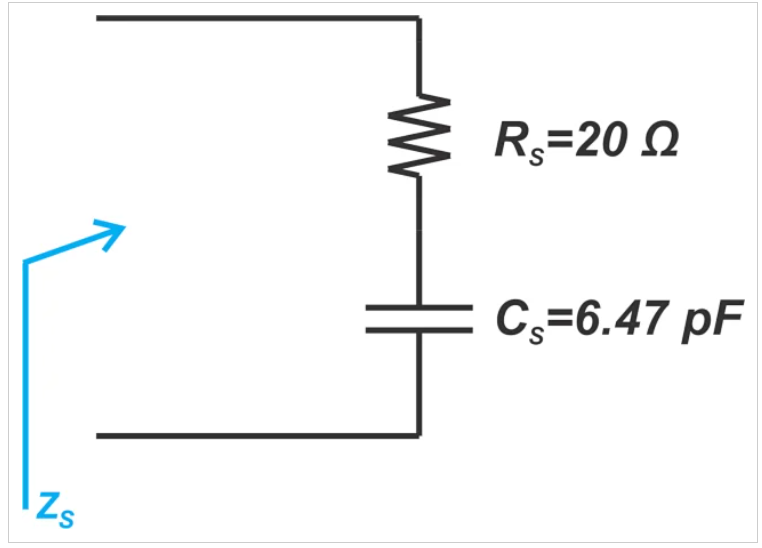
圖6 RS=20Ω和CS=6.47pF的等效串聯電路

圖7中以極坐標形式繪制了兩個電路的輸入阻抗。

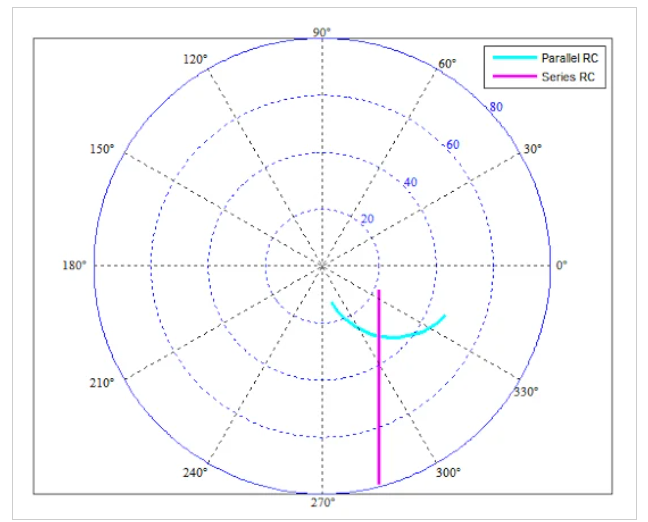
圖7 并聯和串聯RC電路的輸入阻抗

極坐標圖使我們能夠通過一條曲線顯示阻抗實部和虛部的影響。

請注意，阻抗僅在單一頻率下相等（在我們的例子中，在對應于1 GH的兩條曲線的交點處）。在該頻率下，輸入阻抗計算為ZS=ZP?20-j24.12Ω。如果我們考慮大約1 GHz的窄頻率范圍，我們可以假設這兩個電路具有相同的輸入阻抗。

示例2：使用串并聯轉換設計匹配網絡

使用前一個例子的結果設計一個匹配網絡，在1 GHz下將RL=50Ω轉換為20Ω。

在前面的例子中，我們看到RP=50Ω和CP=3.88 pF的并聯RC電路等效于RS=20Ω和CS=6.47 pF的串聯RC電路。基于這些信息，我們可以將3.88 pF電容器與RL=50Ω并聯，以產生所需的20Ω電阻部分。我們只需要從等效串聯電容器（CS）中消除無功分量。CS=6.47 pF的電抗在1 GHz時約為-j24.12Ω。我們可以使用3.84nH的串聯電感器來產生約+j24.12Ω的電抗。這個串聯電感器抵消了CS的電抗，使我們的純電阻阻抗為20Ω。最終的匹配網絡如圖8所示。

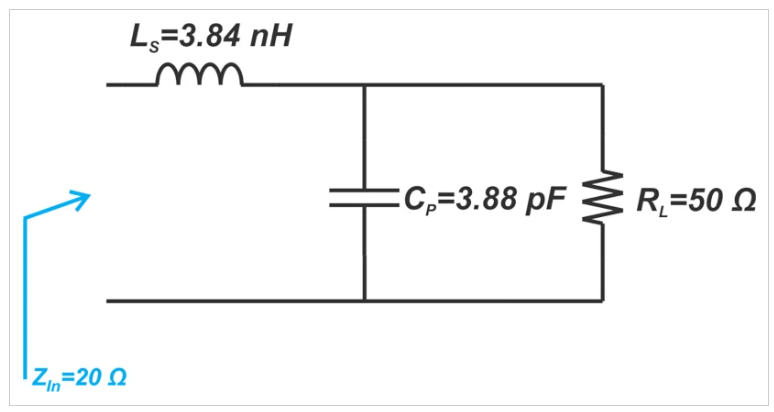
圖8 匹配網絡圖示例

現在我們已經建立了品質因子和串并聯轉換的概念，我們可以討論設計阻抗匹配網絡的分析方法。

兩個電阻端子的L形阻抗匹配

二元無損匹配網絡，稱為L形，廣泛應用于射頻電路中。我們在上述示例（圖8）中設計的電路實際上是一個L形匹配網絡。現在讓我們看看如何為任意負載（RL）和源（RS）阻抗設計這些匹配網絡。為了將RL轉換為RS，我們可以想象兩種不同類形的解決方案，如下圖9所示。

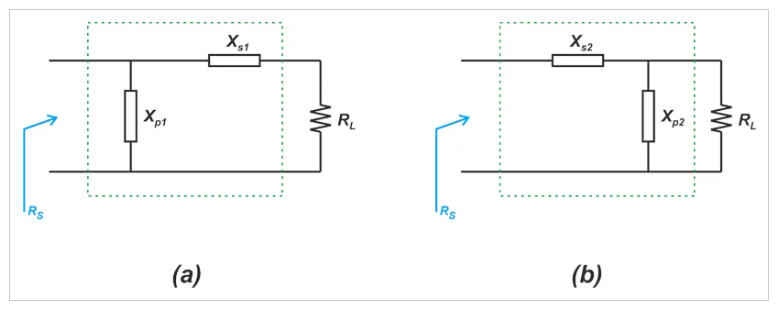
圖9 任意負載（RL）和源（RS）阻抗解的示例電路

在上圖中，X分量表示匹配元件的電抗。對于給定的RL和RS，只能使用上述解決方案之一。為了確定正確的選擇，讓我們應用串并聯轉換。這在圖10中產生了以下等效圖。

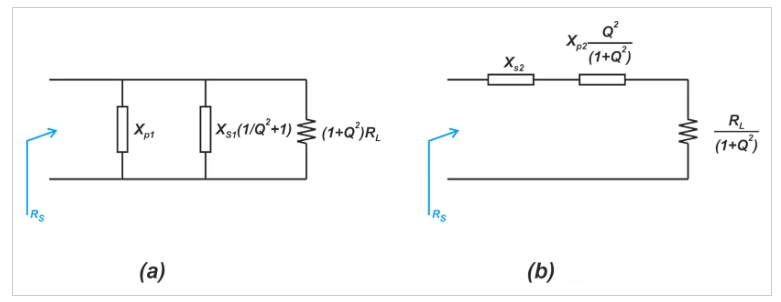
圖10 將串并對話應用于圖9后的兩個示例等效圖

圖10（a）中電路的電阻部分是RL的（1+Q2）倍，而圖10（b）中電路中的電阻部分等于RL除以（1+Q2）。這意味著圖9（a）中的電路將RL轉換為更高的電阻；然而，圖9（b）中的電路將RL轉換為較低的電阻。因此，在設計L形截面時，串聯元件應連接到電阻較小的端子。因此，L形截面的并聯組件應連接到具有較大值的端子。根據我們迄今為止開發的洞察力，我們可以采取以下步驟來設計L形截面：

 1.用較大的值RHigh和另一個RLow命名終端。并使用以下方程式計算電路的品質因子：

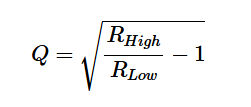
方程式8

2.在RLow旁邊放置串聯電抗元件，在RHigh旁邊放置并聯元件。這將產生兩個子網絡：一個串聯，另一個并聯，如圖11所示。

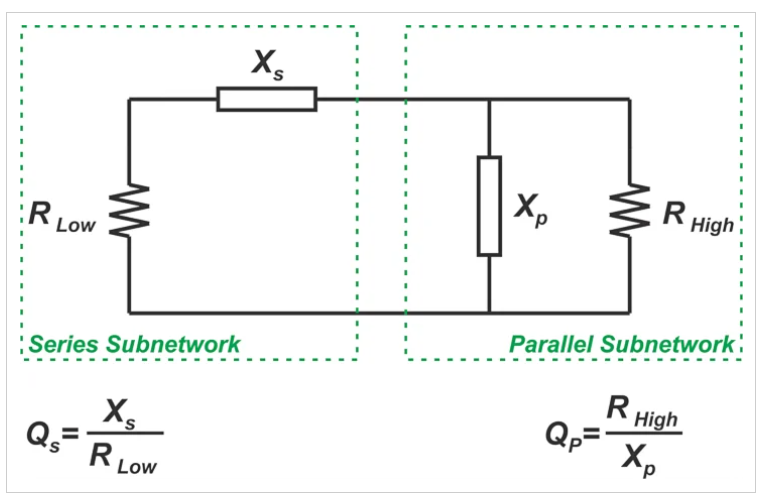
圖11 示例串聯和并聯子網絡

上圖還提供了串聯和并聯子網絡的Q方程。在匹配發生的頻率處，子網絡的品質因子與方程8給出的品質因子相同，即QS=QP=Q。

請注意，在上述電路圖中，輸入電壓源實際上為零，因為這里的目的是提供負載和源阻抗之間的匹配。最終電路圖實際上包括與RLow或RHigh串聯的電壓源（下圖12顯示了最終電路）。

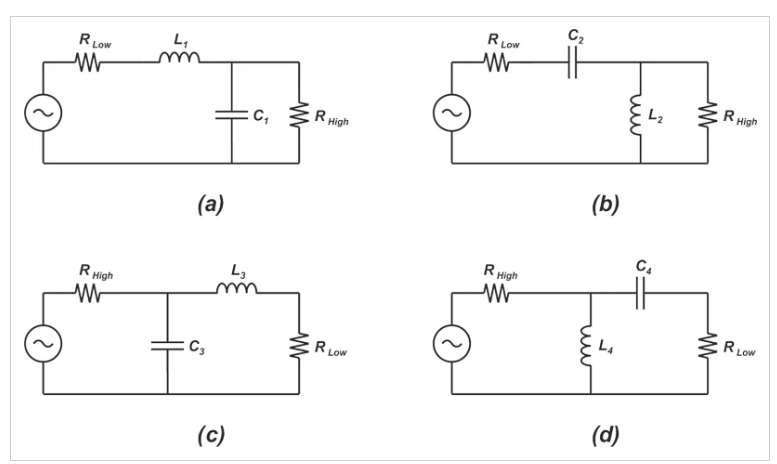
圖12 匹配兩個電阻阻抗的示例

3.有QS、QP和終端電阻，我們可以找到電抗值XS和XP。最后，在感興趣的頻率下計算電感器和電容器值。

注意，XS和XP可以是電容器或電感器；然而，它們不是同一類形的。換句話說，要將純電阻負載轉換為另一個純電阻阻抗，我們需要一個由電感器和電容器組成的L形截面。由兩個電容器或兩個電感器組成的L形截面不能提供兩個電阻阻抗之間的匹配。因此，如下圖12所示，在提供兩個電阻阻抗之間的匹配時，總共有四種不同的選項。

讓我們來看一個例子。

示例3：使用Q因子設計和轉換匹配網絡

設計一個匹配網絡，在1 GHz下將RL=10Ω轉換為50Ω。

通過應用方程式8，可以找到所需的品質因子：

將串聯元件放置在RL（較低電阻）旁邊，我們得到以下L形截面（圖13）：

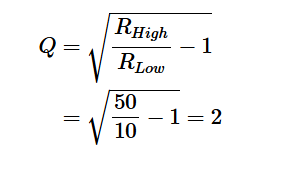
在RL旁邊放置一個系列組件后的L形截面。

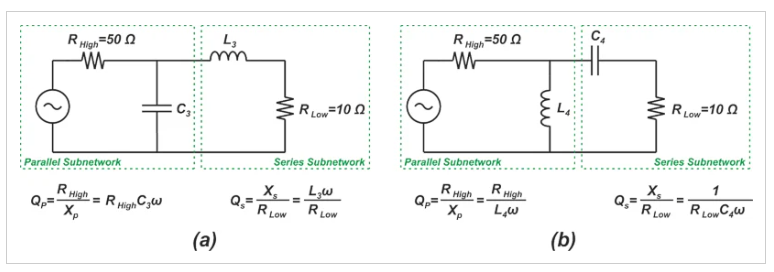
圖13 在RL旁邊放置一個系列組件后的L形截面

對于圖13（a）中的電路，我們有：

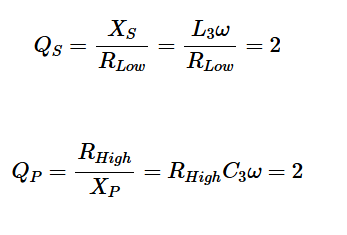
在1 GHz下，上述方程產生L3=3.18 nH和C3=fc6.37 pF。對于圖13（b）中的電路，我們有以下方程組：

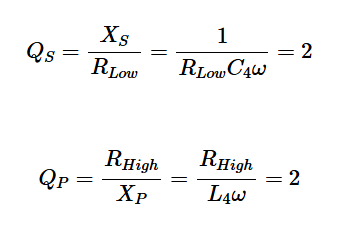
在1 GHz下，分量值為C4=7.96 pF和L4=3.98 nH。

L形匹配網絡設計總結

L形匹配網絡可以使用基于史密斯圓圖的圖形方法或一些簡單的方程來設計。在這篇文章中，我們推導了分析方法的方程，并看了一些例子。阻抗匹配網絡設計的一個關鍵步驟是RL和RC電路的串并聯轉換。值得一提的是，串并聯轉換也有助于分析組件模形，以發現不同類形損耗的組合效應。