今天給大家分享的是：有源濾波器、包含有源濾波器原理分析、拓撲結構介紹、品質因素Q計算。

一、有源濾波器

有源濾波器將有源元件引入濾波電路，有源元件是由外部電源單獨供電的組件，而不是由信號本身供電。

通過在濾波器后添加緩沖運算放大器，可以用信號驅動更高的負載而不會衰減，例如下面的高通濾波器示例：

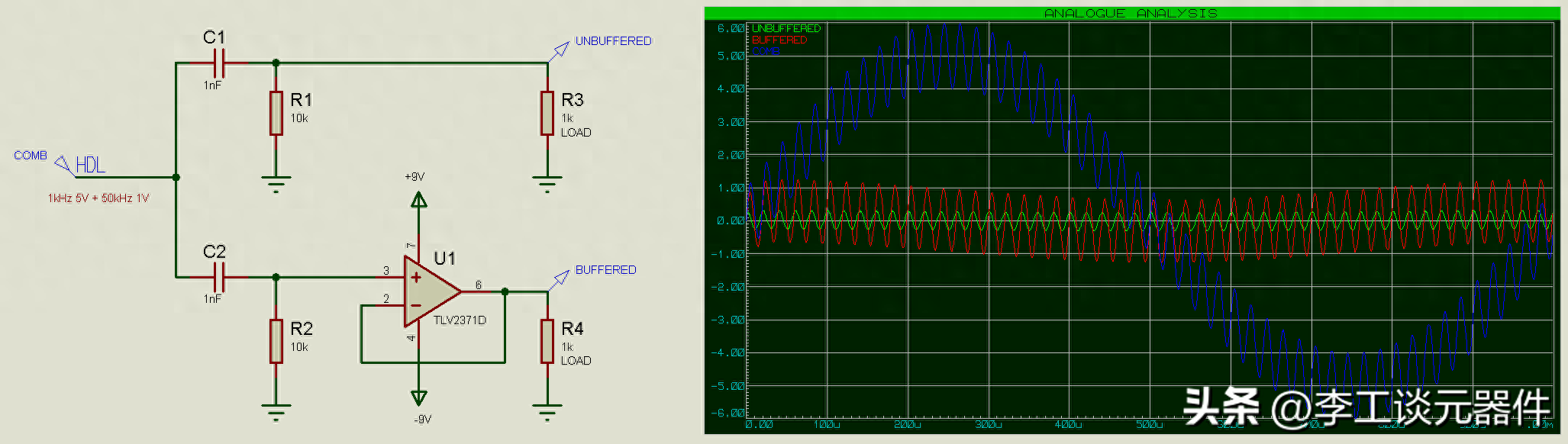
有源濾波器

注意：與緩沖輸出（紅色跡線）相比，未緩沖輸出（綠色跡線）顯著衰弱。

二、為什么要使用有源元件?

在高階濾波器鏈中添加緩沖運算放大器還可以減少鏈中每個環節之間的衰減，并防止鏈中的濾波器元件扭曲鏈中其他濾波器元件的濾波器特性。

例如，我們看下面的二階低通濾波器，那么可以看到，第二個濾波器的電阻元件不僅僅是R2=10k，而是 R1 + R2 = 20k。而第一個濾波器中的電容，不僅需要考慮C1的電容，還需要考慮C2的電容。

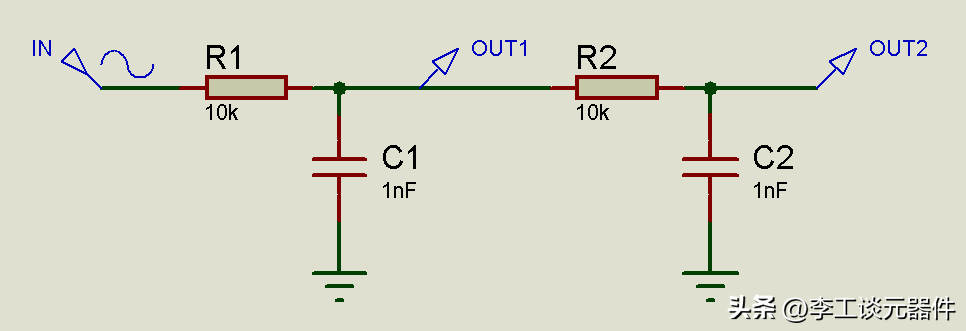
二階低通濾波器

截止頻率公式：F= 1/2πRC

這具有降低濾波器截止頻率的效果。

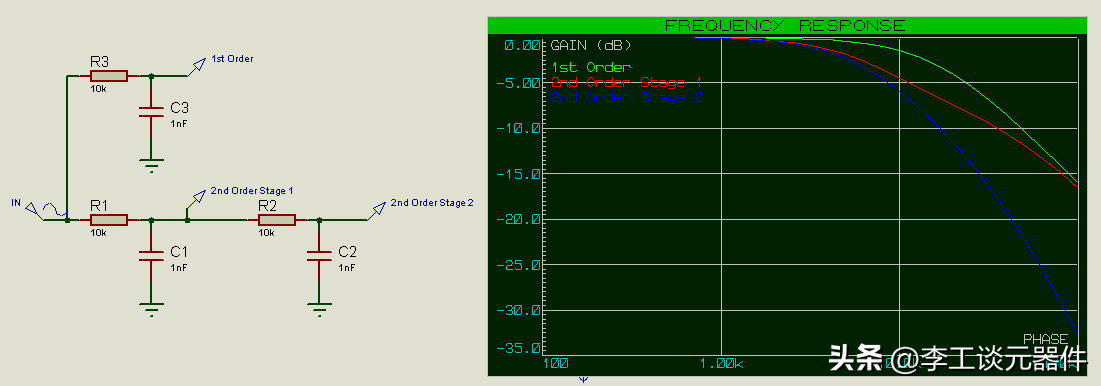
降低濾波器截止頻率

對于10k 和 1nF 的 R 和 C 值，預計截止頻率（第一濾波器級為 -3dB，第二濾波器級為 -6dB）為 15.9kHz，但發現它略低于該值。

這里要注意，二階階段1的頻率響應如何遵循二級階段2的頻率響應。在低頻下，電容充當開路，但在較高頻率下，二階級1跟在一階濾波器之后，因此C1開始充當短路電路，其電阻（與 R2 相比）較低。

如果我們在濾波器第二級中降低電阻并增加電容（但保持相同的 RC 常數），這種情況會更加明顯：

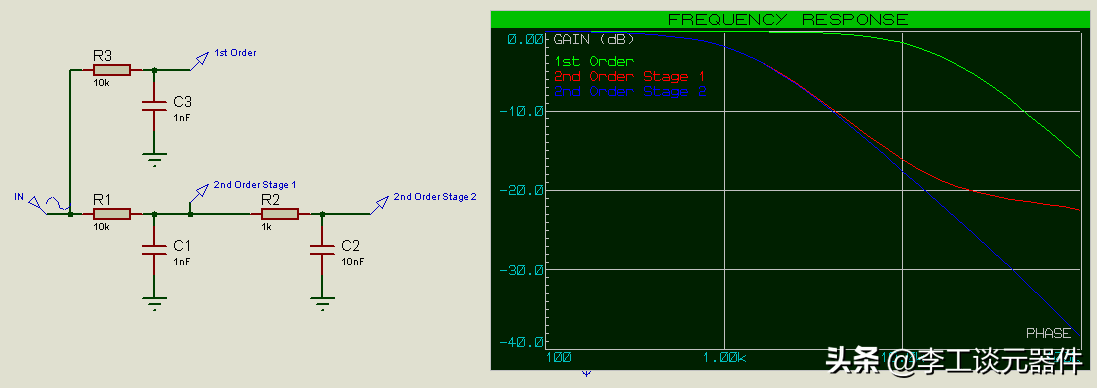
在濾波器第二級中降低電阻并增加電容

這樣的話，截止頻率會變得更低。

緩解這種情況的一種方法是讓第二級的輸入阻抗至少比第一級的輸出阻抗大一個數量級（10x），即使R2 比 R1 大 10 倍（并使 C2 小 10 倍） ，保持 RC 恒定）。

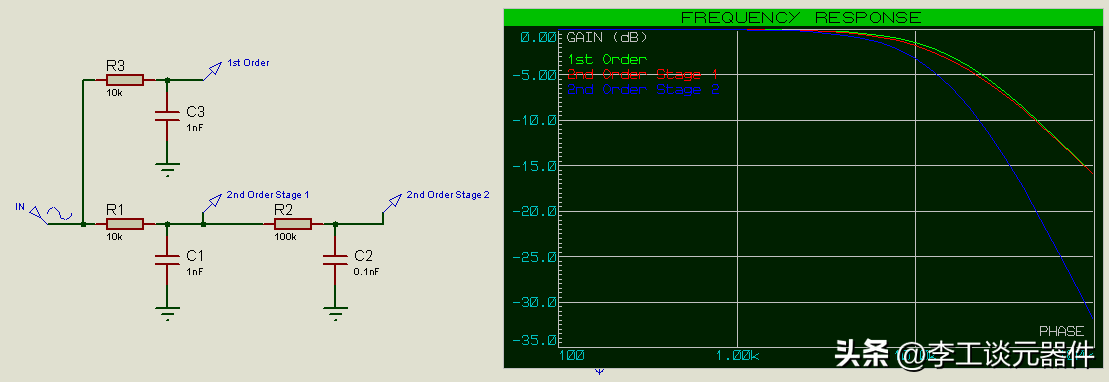
二階濾波器第一級的頻率響應與一階濾波器的頻率響應非常匹配

現在可以看到二階濾波器第一級的頻率響應與一階濾波器的頻率響應非常匹配。截止頻率也更接近預期的 15.9kHz。

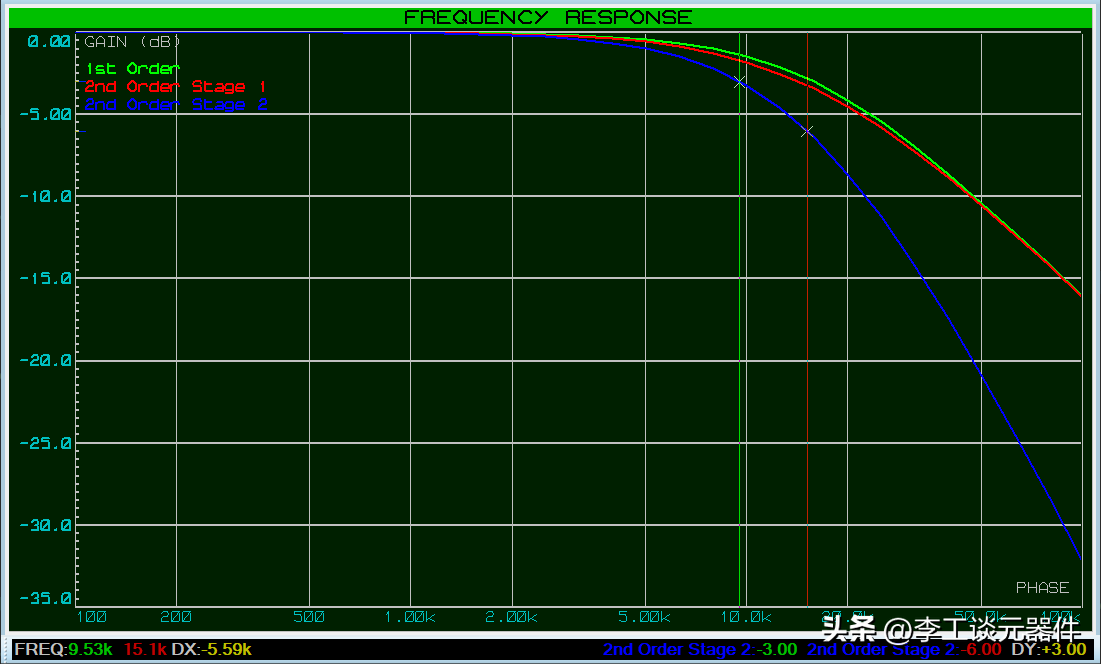
截止頻率也更接近預期的 15.9kHz

進一步降低第一級的輸出阻抗和/或增加第二級的輸出阻抗，就會讓截止頻率更接近預期，但是不會完全達到預期。

如果增加第三（或第四等）過濾器階段，問題就會更復雜，這就是為什么要添加緩沖運算放大器原因。

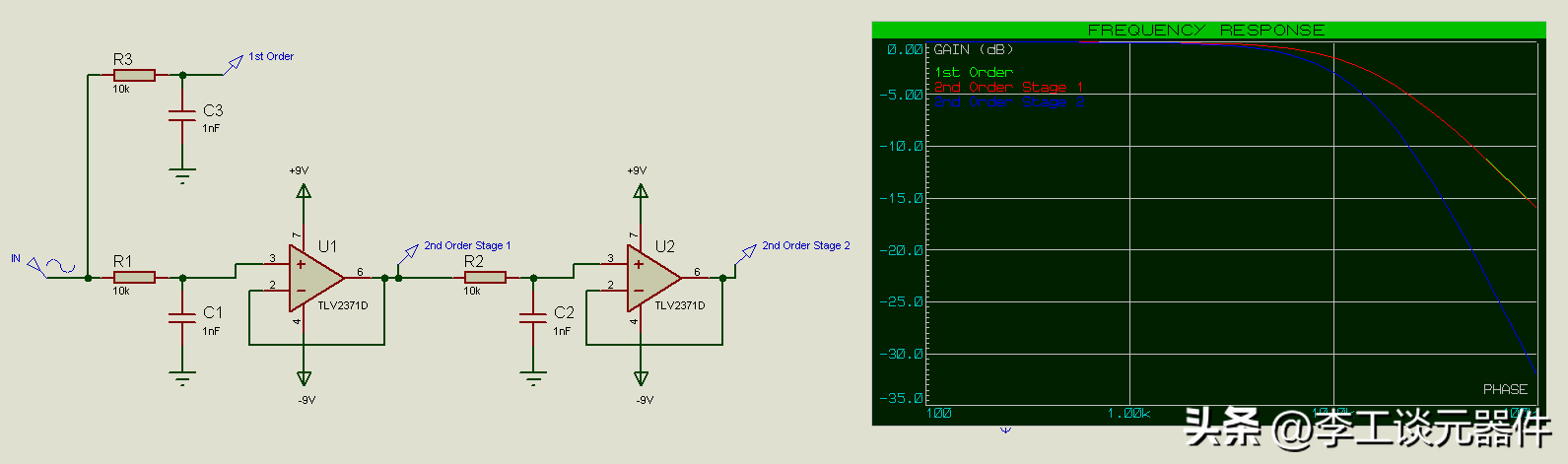
添加緩沖運算放大器

在這種情況下，我們可以看到二階濾波器的階段 1 與一階濾波器的階段 1 完全匹配，并且截止頻率如預期為 15.9kHz。

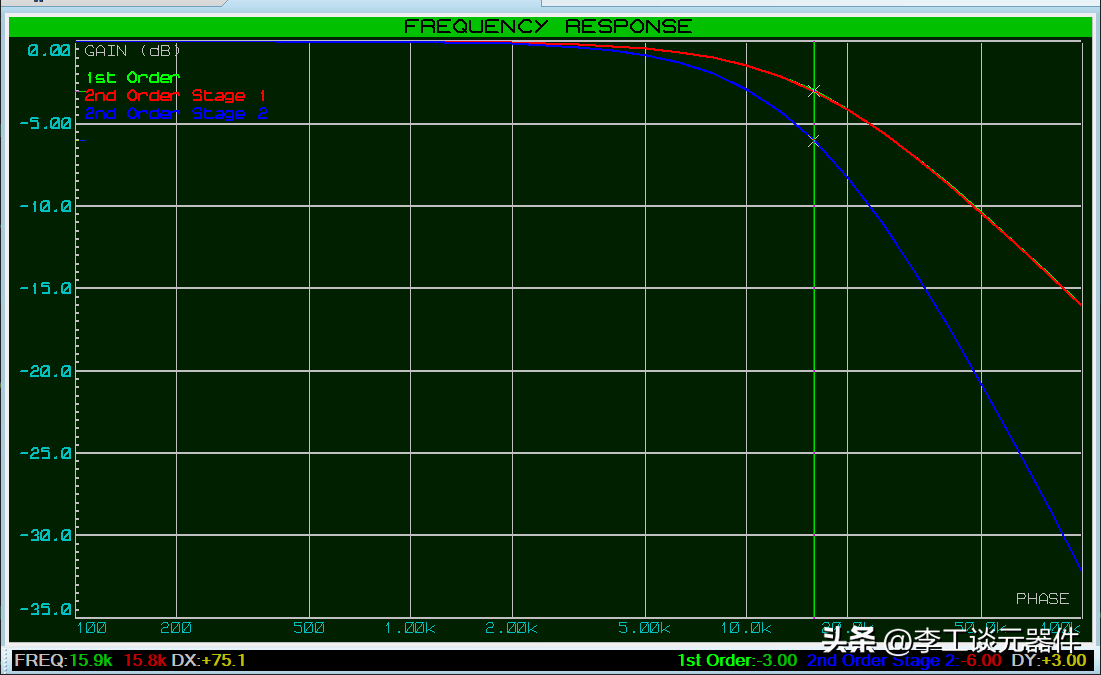
并且截止頻率如預期為 15.9kHz。

可以根據需要添加額外的濾波器級，以獲得所需的滾降清晰度。

注意：每添加一個附加濾波器級，截止頻率處的衰減（以 dB 為單位）就會增加 -3dB。一階濾波器在截止頻率處的衰減為-3dB，二階濾波器為-6dB，三階濾波器為-9dB，等等。

三、Sallen-Key拓撲結構

Sallen-Key 拓撲是一種二階濾波器拓撲，它使用單個運算放大器。

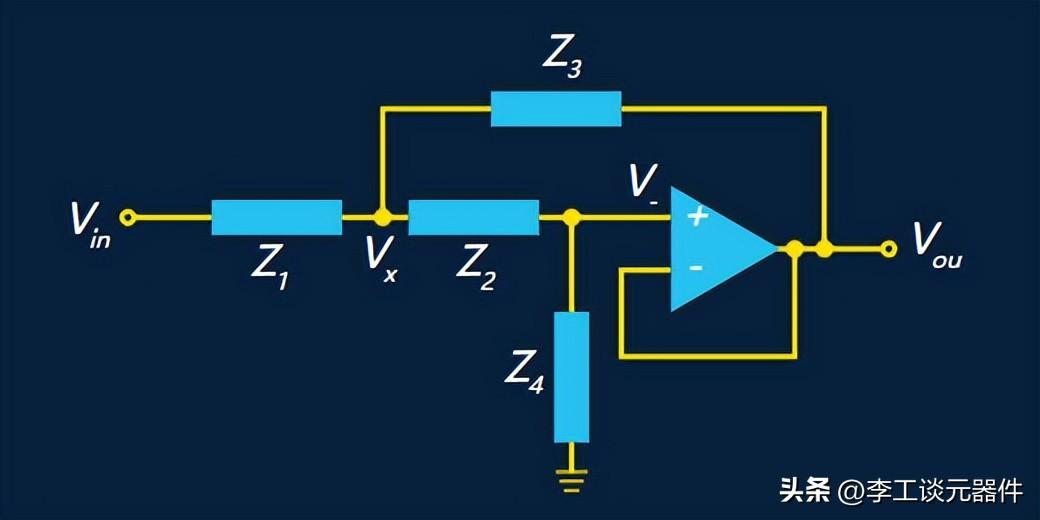
Sallen-Key 拓撲

Z 元件的選擇取決于是否需要低通、高通、帶通或帶阻濾波器。

1、低通Sallen-Key濾波器

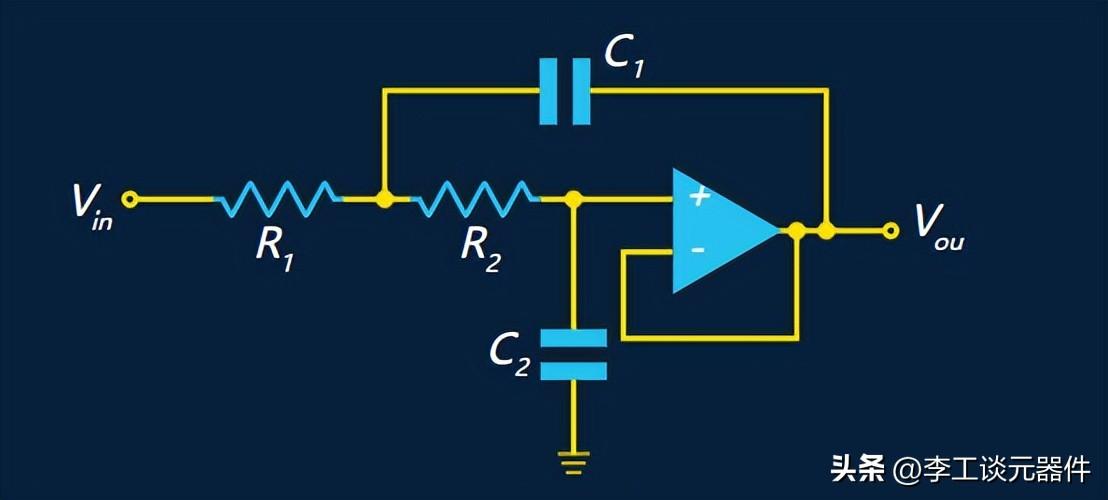
低通Sallen-Key濾波器

2、高通Sallen-Key濾波器

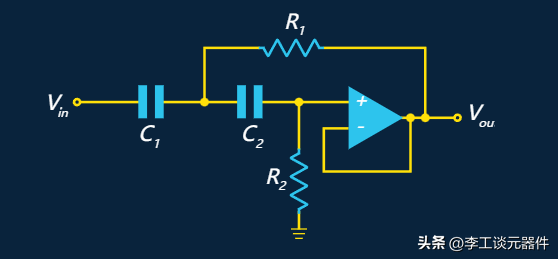
高通Sallen-Key濾波器

3、帶增益的Sallen-Key濾波器

還可以選擇添加增益（在運算放大器的反相輸入上使用分壓器）

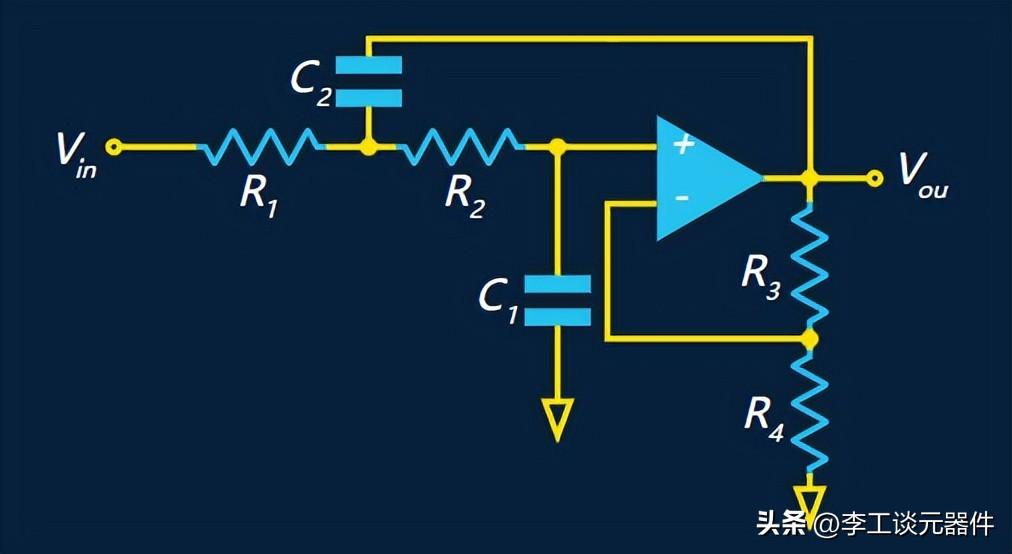
帶增益的Sallen-Key濾波器

Sallen-Key 濾波器獨特的特征是：第一級不連接到地，而是連接到運算放大器的輸出。這會將運算放大器輸出的反饋添加回正輸入，可用于增加濾波器的“Q”。

四、品質因素 Q

振蕩系統的品質因數或 Q 描述了它的阻尼程度（從技術上講，它的阻尼不足程度 - 與阻尼相反）。

在空氣中擺動的鐘擺比在水中擺動的鐘擺具有更高的 Q 因子；在空中擺動的鐘擺在每次擺動時因阻力而損失的能量較少，因此擺動的時間更長。

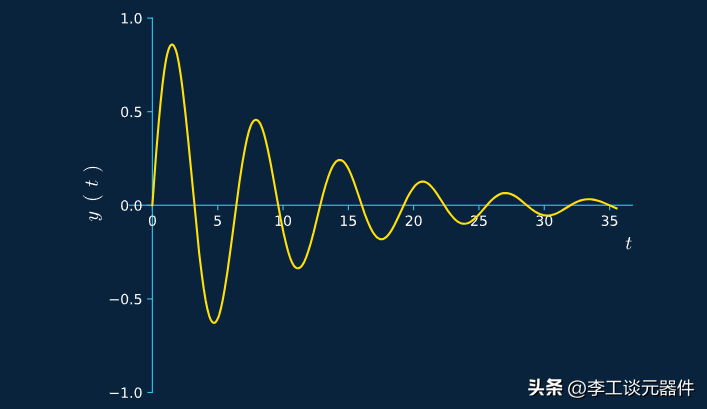
品質因素 Q

• Q = 1 意味著沒有阻尼/欠阻尼，并且信號的幅度保持完全相同。

• Q > 1 意味著信號被放大（增加）。

• Q < 1 意味著信號衰減（減少）。

就濾波器響應而言，濾波器的 Q 值描述了它在截止頻率（下圖中的 10kHz）附近的情況：

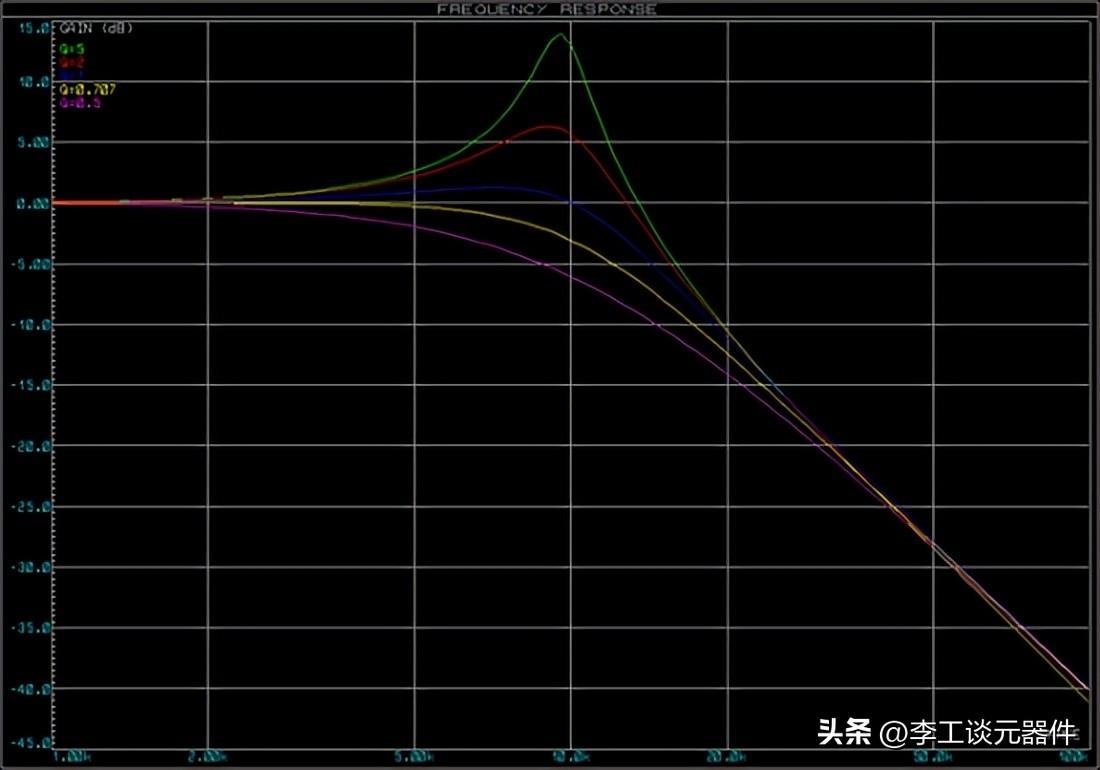
濾波器的 Q 值

• Q > 1 將放大截止頻率處的信號。

• Q = 1 將在截止頻率處保持信號幅度相同。

• Q < 1 將衰減截止頻率處的信號。

注意：Q 值越高，截止頻率處的拐角越尖銳。無源一階濾波器的 Q 值為 0.707 (-3dB)，無源二階濾波器的 Q 值為 0.5 (-6dB)。

然而使用 Sallen-Key 有源濾波器拓撲，我們可以為應用選擇 Q 值，例如希望Q 為 1，這樣濾波器可以使信號不衰減更接近截止頻率，然后具有更尖銳的滾動-在截止頻率處截止。

其工作原理是：將輸出的濾波信號反饋到輸入信號，在截止頻率附近與其諧振，從而增加其幅度（從而增加 Q）。

五、低通計算

在線和離線計算器可以計算給定截止頻率、Q 和增益的 R 和 C 值。這里，簡要地看一下情況，其中增益為 1（單位），電阻和電容設置為彼此的比率。

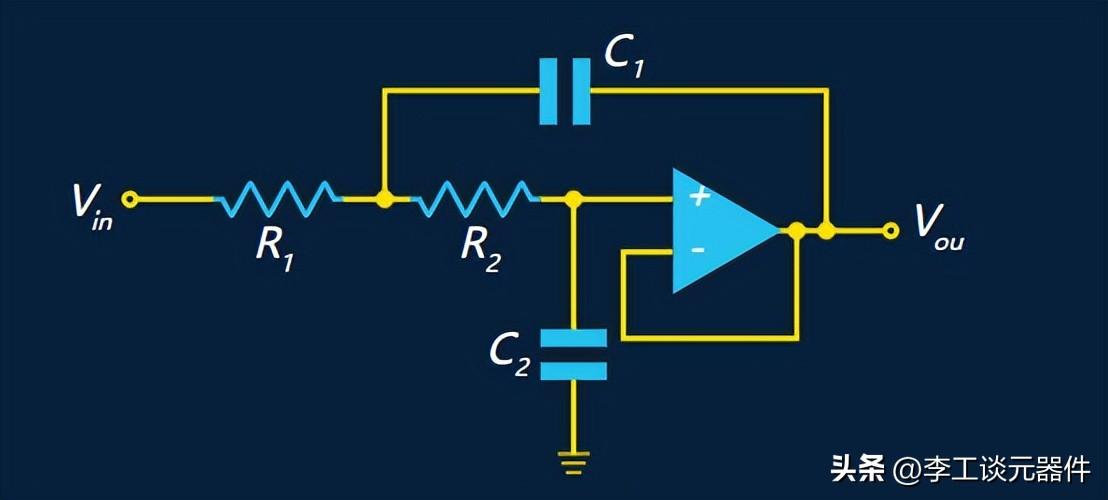
低通Sallen-Key濾波器

R2 = xR1, 且 C2=(1/x)C1

當我們創建一個 2 級無源濾波器來減輕對截止頻率的影響），截止頻率的公式仍然是 1 / 2πRC。

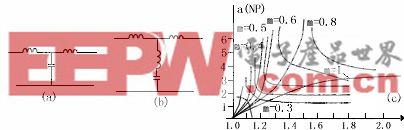
Q = x / (x + 1)

由此我們可以看出，如果 x=1（兩個階段的分量值相同），那么我們得到的 Q 為 1 / (1 + 1) = 1/2 = 0.5；

這與我們使用通常的 2 級濾波器 (-6dB) 得到的 Q 值相同。

然而，如果我們將 x 增加到 10，那么我們得到的 Q 為 10/11 = 0.91，這比我們之前的值要高得多。

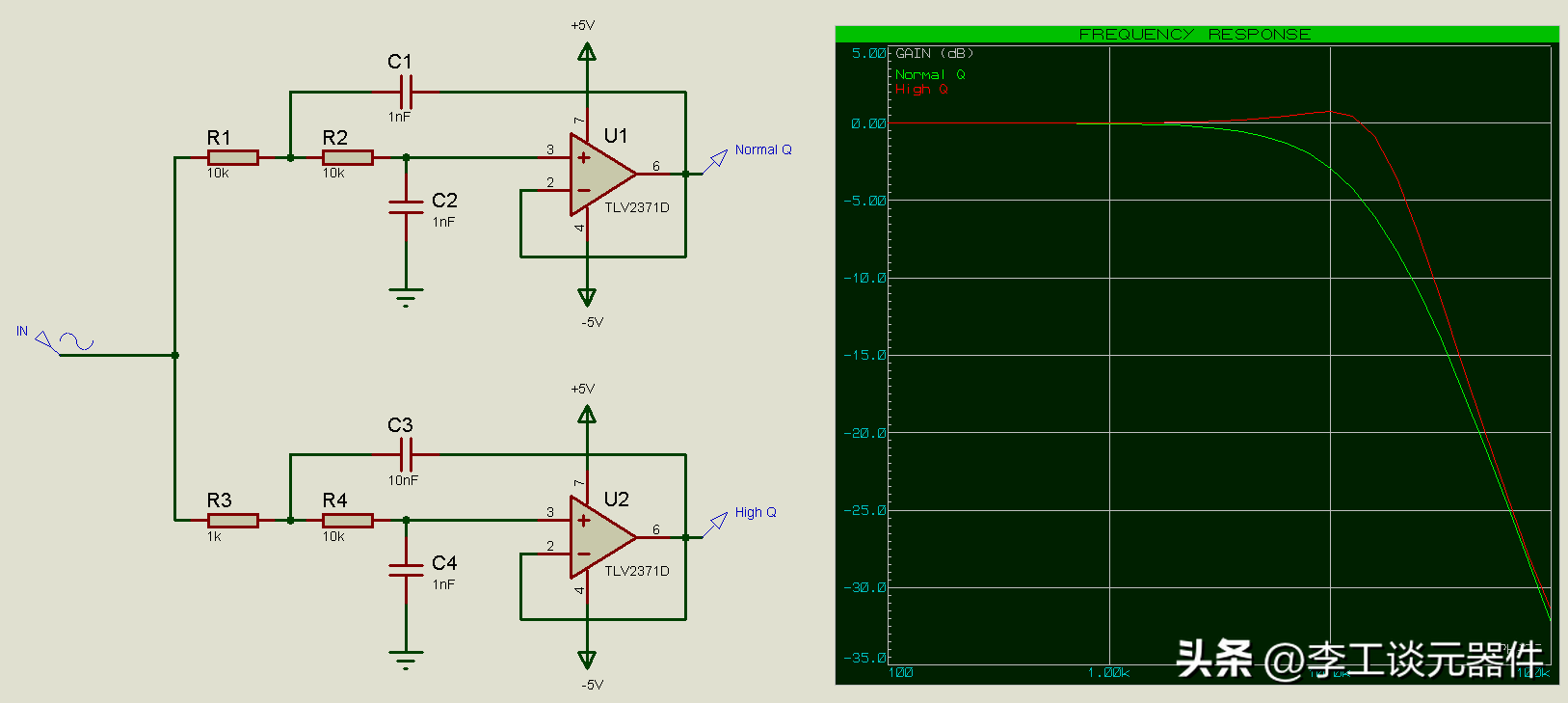
將 x 增加到 10

六、高通計算

計算都是同樣的原理：

R2 = xR1，且 C2=(1/x)C1

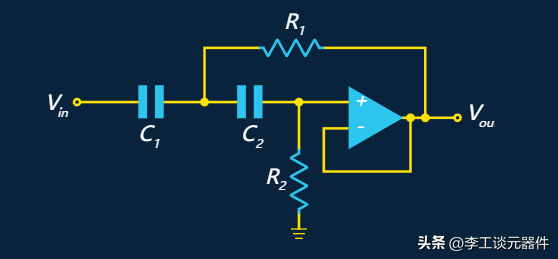
高通

對于 x = 1，我們再次得到 Q = 0.5，對于 x = 10，我們再次得到 Q = 0.91。

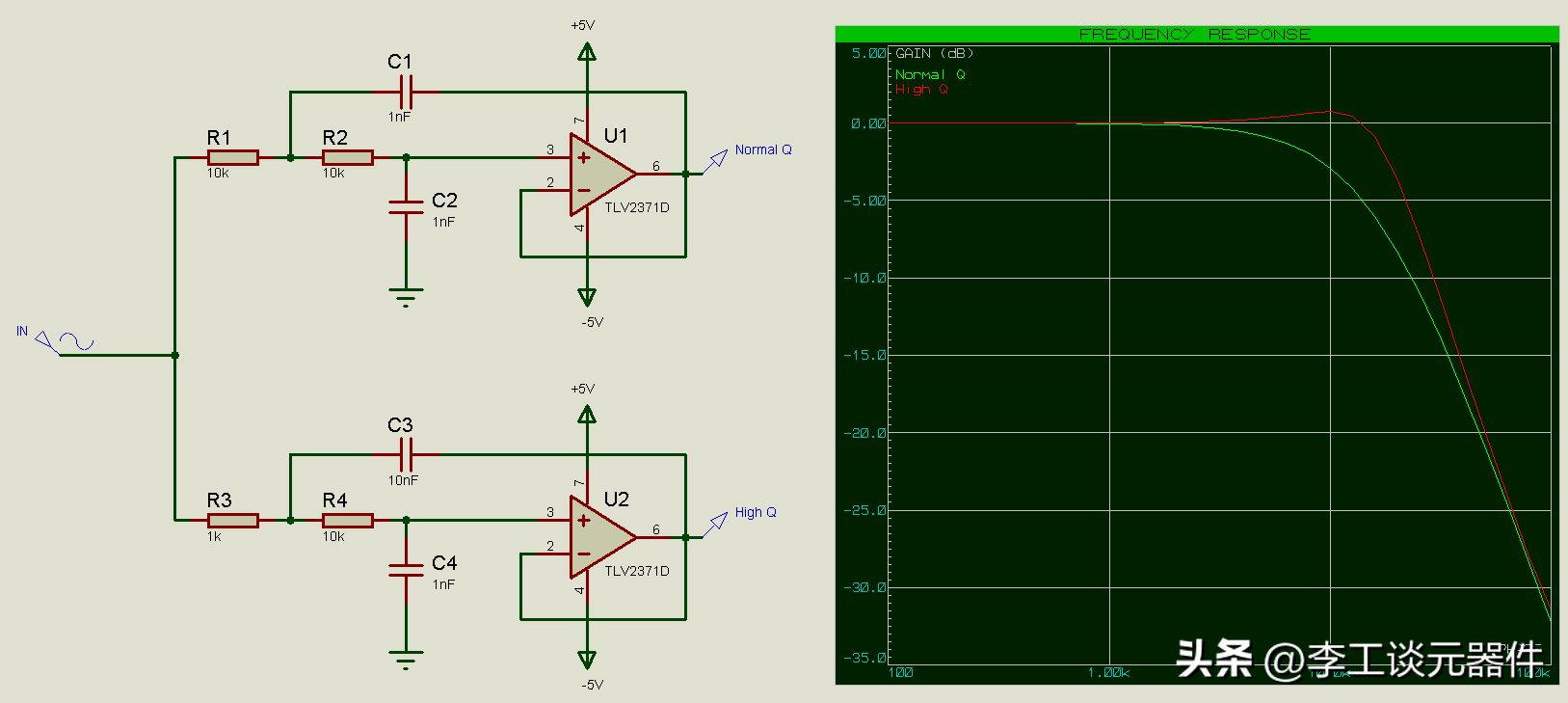
x 增加到 10

原文鏈接：https://www.labcenter.com/blog/sim-active-filters/