利用復磁導率表征磁芯損耗

在這篇文章中，我們使用磁場強度的概念來幫助解釋復雜磁導率如何模擬磁芯的損耗。

磁導率是用于電氣元件的鐵磁材料的一個關鍵參數，它將材料內部的磁場與外部場聯系起來。在非常低的頻率下，實值磁導率可以描述材料的磁化強度。然而，在更高的頻率下，磁性材料制造商使用復雜的磁導率值。這種復雜滲透率的想象部分可以解釋巖心損失——但如何解釋呢？

在這篇文章中，我們將深入研究復磁導率的理論。我們將從研究磁場強度的概念開始討論，這對以后理解一些數學知識至關重要。請注意，當我們在本文中提到“磁性材料”時，我們具體指的是鐵磁材料。

磁場強度

本系列先前的文章指出，對于置于均勻磁場（B0）中的材料，材料內部的總磁場由下式給出：

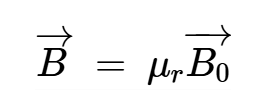
等式1。

其中μr是材料的相對磁導率。

當分析磁場對材料的影響時，我們需要不斷區分B0和B。為了使這種區分更清楚，我們將定義另一個場量——磁場強度，用H表示。

磁場強度定義為外部施加的磁場除以自由空間的磁導率（μ0）：

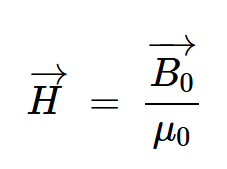
等式2。

使用這個新的場量，方程1可以重寫為：

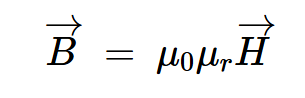
等式3。 

乍一看，引入一個新的數量可能是多余的，但這實際上是一種方便的方式來澄清我們指的是哪個字段。我們使用H和B字段的特定名稱來強調它們之間的以下差異：

H是磁場強度（或強度）。

B是磁通密度，有時是磁感應。

讓我們來看一個例子。

示例：電磁閥的磁場強度

考慮圖1中的電磁閥。

一個具有N匝和長度為l的示例螺線管。

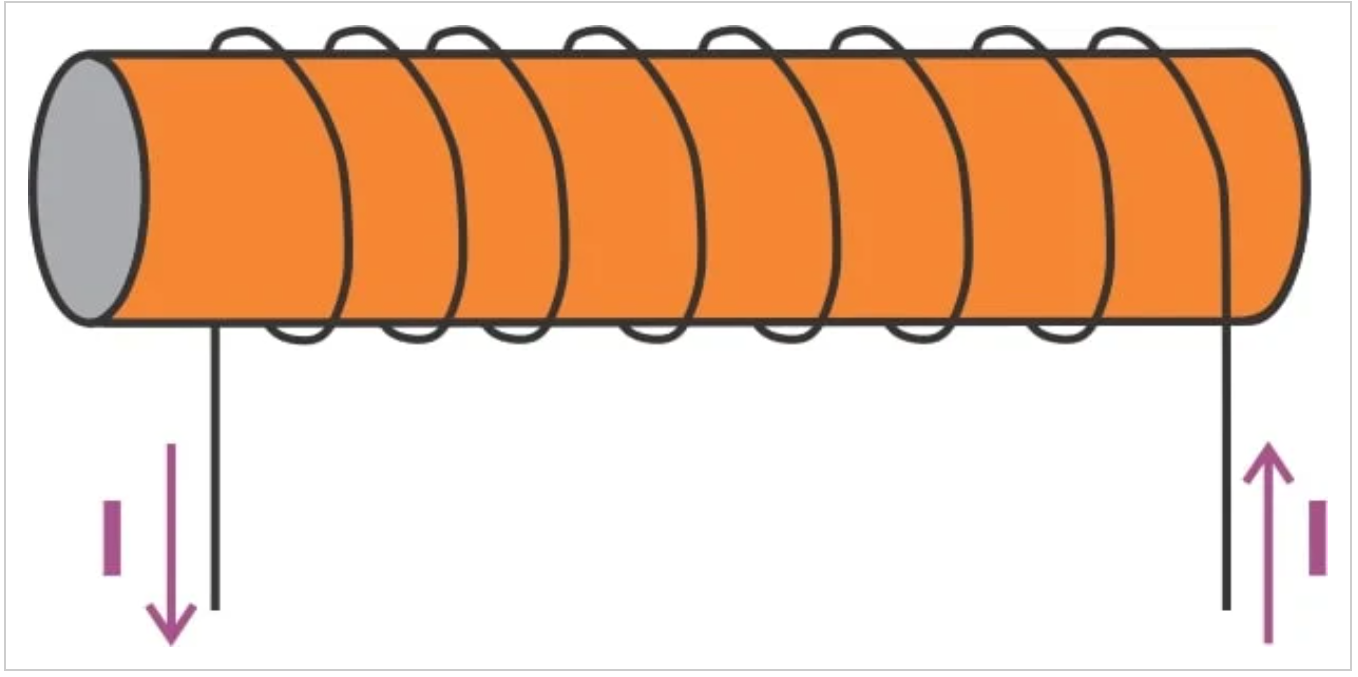
圖1。電磁閥示例。圖片由Steve Arar提供

我們想回答兩個問題：

當不使用磁芯時，這個螺線管的磁通密度（B）和磁場強度（H）是多少？

當我們插入具有相對磁導率μr的磁芯時，通量密度是如何變化的？

假設匝間間隔很近，線圈內部的場是均勻的，我們可以應用安培定律來找到線圈內部的電場。在不詳細介紹這些步驟的情況下，空心螺線管的最終結果是：

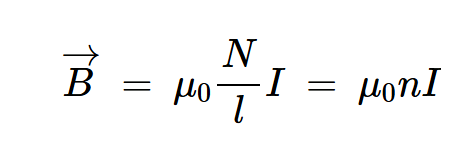
等式4。

解釋

N是總匝數

l是螺線管的長度

l是電流

n是每單位長度的匝數。

因為沒有使用磁芯，所以方程4中描述的磁場由通過線圈的電流產生，而沒有磁芯磁化的任何貢獻（B＝B0）。將該值除以μ0得出磁場強度：

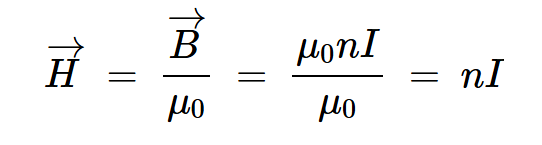
等式5。

如果我們插入一個磁芯，磁通密度變為：

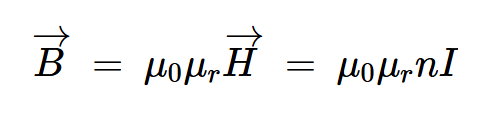
等式6。

由于磁芯的存在，B現在包括兩個磁場分量：

電流產生的磁場。

由核心材料的磁化產生的磁場。

磁場強度本身是由電流產生的，因此可以認為是產生磁通密度的驅動力。滲透率量化了H產生B的容易程度。

磁芯如何改變電感？

接下來，讓我們看看當我們插入磁芯時，空心螺線管的電感是如何變化的。電路的電感（L）定義為每單位電流流過電路時通過電路的總磁通量。對于空心螺線管，我們有：

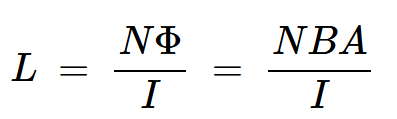
等式7。

解釋

Φ是通過每一圈的磁通量

I是流過線圈的電流

A是電磁閥的橫截面積。

由于沒有磁芯，我們有

→B = μ0→H

.插入磁芯可使磁通密度增加μr。

例如，假設核心材料的滲透率是自由空間滲透率的500倍。對于給定的電流，使用該磁芯將線圈內部的場增加500倍。等式7示出了線圈的電感也以相同的因子增加。

基于以上內容，如果空心螺線管的電感為L0，則具有磁芯的同一螺線管的電感將為：

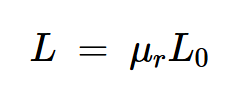
等式8。

現在我們知道了磁芯是如何改變電路電感的，我們可以使用方程8來了解它是如何改變阻抗的。由于理想的空心螺線管充當電感為L0的電感器，因此其阻抗為：

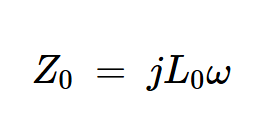
等式9。

當插入磁芯時，電感——以及阻抗——乘以相對磁導率，得到：

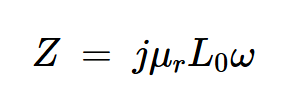
方程式10。

巖心損失的核算：復雜滲透率

到目前為止，我們已經假設核心是無損的。這就是為什么方程10產生純電感阻抗，我們知道它耗散零平均功率。事實上，一些輸入能量將作為熱量在堆芯中損失。我們如何對這些核心損失進行建模？

注意到電阻器是表示損耗的電氣元件，我們需要一種方法，在上面的阻抗方程中包括一個額外的電阻項。方程中唯一的核心性質是滲透率，所以這是我們要修改的參數。正如你可能已經猜到的那樣，我們需要將滲透率定義為一個復雜的值來解釋巖心損失。復雜滲透率的方程式為：

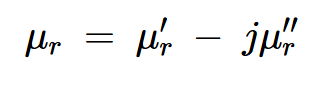
等式11。

通過將復磁導率代入方程10，我們得到：

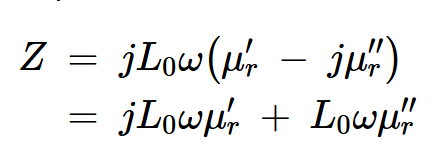
方程式12。

現在，我們的阻抗方程中有兩個不同的項：

一個源自磁導率（μr′）實部的歸納項。這個術語表明磁芯增加了通過線圈的磁通量，從而增加了其電感。

源自磁導率虛部（μr〃）的電阻項。這個術語與材料的損失有關。

方程12得出了圖2所示電感器的等效電路模型，該模型由一個理想的電感器與一個電阻器串聯組成。

鐵芯損耗串聯表示的等效電路模型。

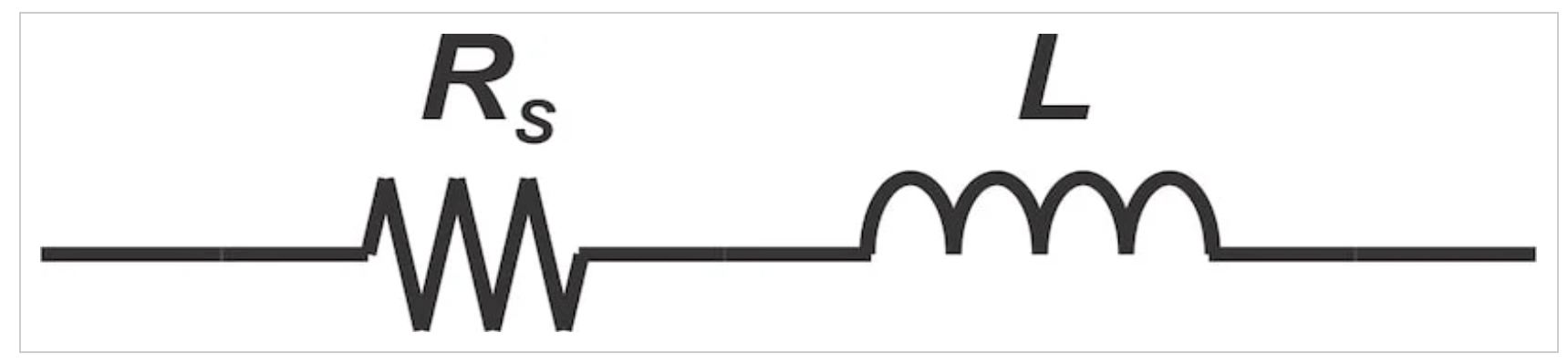
圖2:鐵芯損耗串聯表示的等效電路。圖片由Steve Arar提供

如果將圖2中的串聯電路模型轉換為其并聯等效電路，則并聯電阻也將模擬核心損耗。

磁化與外加磁場異相

我們在方程11中定義了復磁導率。讓我們看看這個等式到底意味著什么。

我們知道，磁導率描述了施加在磁性材料上的外部場與其內部產生的場之間的關系。方程11中磁導率的實部對應于與外部場同相的材料磁化。這是我們對理想無損內核的期望。

另一方面，磁導率的虛部表明，材料的某些磁化與所施加的場發生90度異相。這種相移導致電感器兩端的感應電壓與流過電路的電流同相，從而在整個阻抗方程中產生電阻項。

圖3顯示了兩個不同核心的B和H場之間的相位關系。圖3（a）對應于無損核心，圖3（b）對應于有損核心。

B和H之間的相位關系。

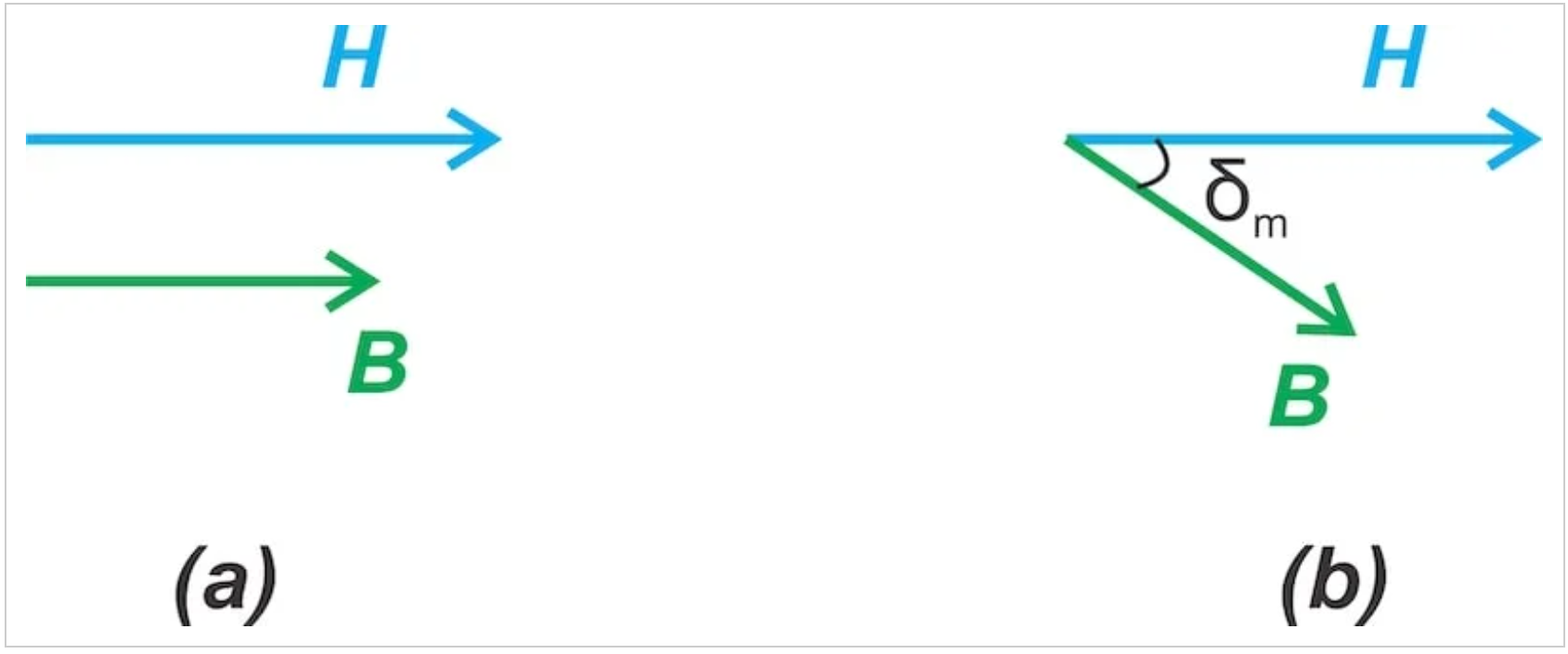
圖3。B場和H場之間的相位關系。圖片由Steve Arar提供

在無損核心中，

$\overrightarrow{B}$