放大電路的頻響分析

在分析放大電路的頻響特性時，實際上解決的是放大電路的低頻截止頻率ωL(或fL)和高頻截止頻率ωh(或fh)與電路結構、元件參數之間的關系問題。

對所設計的放大電路，總希望中頻增益范圍越寬越好。然而，由于有耦合電容和旁路電容的影響，在頻率的低端區增益會下降，而在頻率的高端區，則由于分布電容及晶體管極間電容的影響增益也會下降，這樣放大電路頻帶寬度將會受到一定的制約。通常根據通帶的低端頻率和高端頻率來區分哪些電容對低頻響應起作用，哪些電容對高頻響應起作用，從而分別構造出相應的低頻和高頻的電路模型，以便對電路的頻率響應做出正確的分析。

本文正是通過對放大電路的瞬態響應、穩態響應、以及二者之間關系的分析，較詳細地剖析了放大電路的頻響分析過程，為放大電路的分析和設計提供了必要的分析方法。

01、放大電路的瞬態分析

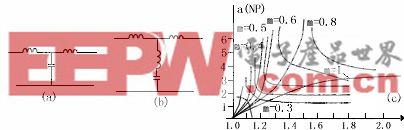
在分析電路瞬態響應時，電路處于非穩定狀態。為了計算方便，對電路的輸入和輸出函數施行拉氏變換，由此求出相應的傳遞函數，由傳遞函數來分析研究電路的傳輸情況。如圖1所示電路，如取電感電壓uL(t)為電路的輸出電壓u0(t)，顯然有

則傳遞函數為

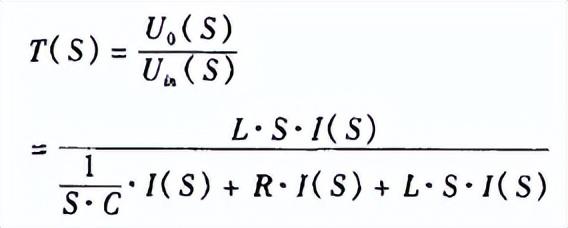
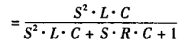
由此可得輸出電壓的時域形式：

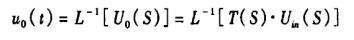
由上分析可知，在電路的瞬態響應分析中，采用傳遞函數來分析研究電路的傳輸情況是非常方便的，由傳遞函數的零極點便可確定電路的傳輸特性。如已知輸入，則輸出電壓u0(t)就完全由代表電路特性的零極點所決定。

02、放大電路的穩態分析

當放大電路進入穩定狀態后，電路中所有變量均為同頻率的周期函數。與研究放大電路瞬態響應一樣，穩態響應中放大電路的傳輸情況也是本文研究的重點。在進行放大電路穩態分析時，需要構造出相應的電路模型，而電路模型是在一定的假設條件下建立起來的。對處于低頻段和高頻段的放大電路來說，在相應的假設條件下所構造的電路模型是不同的。因此，放大電路的低頻穩態響應和高頻穩態響應需分別進行分析。

放大電路的低頻穩態響應

對于低頻段的放大電路來講，由于頻率相對較低，所以，可以忽略晶體管極間電容的影響作用，將該電容看成是開路的。這樣，便構造了放大電路的低頻電路模型。圖2電路便是低頻交流放大電路的電路模型。

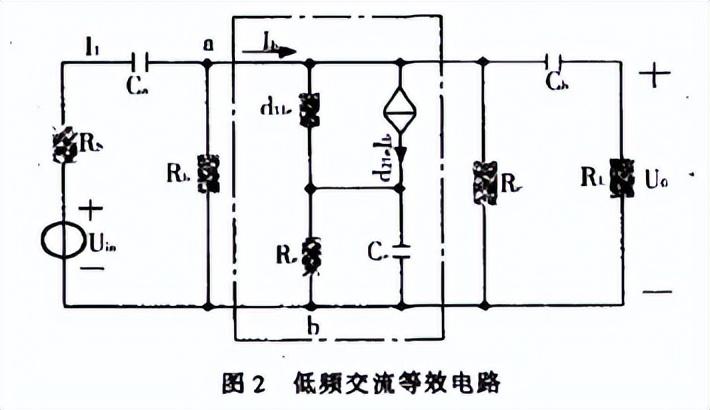
該傳輸系數雖有三個極點，但電路的低頻特性主要是由絕對值最大的極點來決定，即電路的低頻截止頻率等于絕對值最大的極點值。

放大電路的高頻響應

分析放大電路的高頻響應時，需采用高頻電路模型。這時，電路中的分布電容的影響須考慮在內，而可以忽略耦合電容和旁路電容對電路的影響。圖4即為圖2放大電路的高頻交流等效電路。

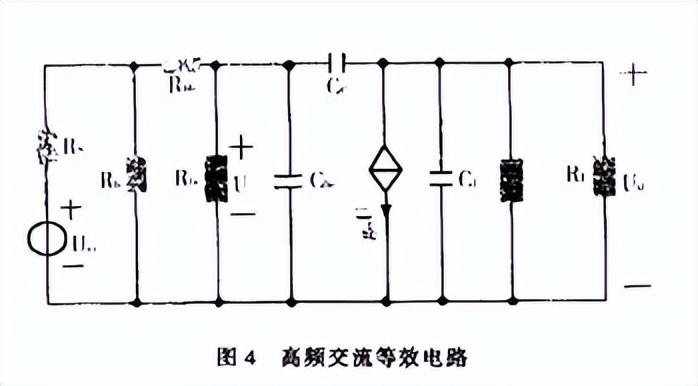
由上分析可知，該電路有一個零點，兩個極點，在給定電路元件參數值的情況下，便可由傳輸系數確定該電路的頻響特性。

03、放大電路的瞬態響應與穩態響應的聯系

以上對放大電路的瞬態響應與穩態響應進行了分析，顯然，二者的分析方法相近。在瞬態響應分析中，電路的輸入和輸出關系是由拉氏變換所確定的傳遞函數來表述的，而在穩態響應分析中，電路的輸入和輸出關系是通過電路的傳輸系數來表述的。那么二者之間有何內在的聯系呢？對于圖1電路來講，由前面分析可知，當該電路處于瞬態響應時，其傳遞函數為:

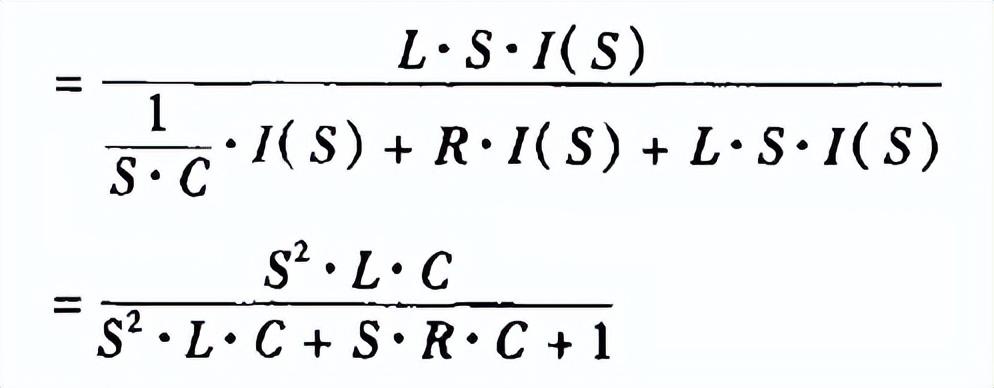
而當該電路處于穩態響應時，其傳輸系數應為：

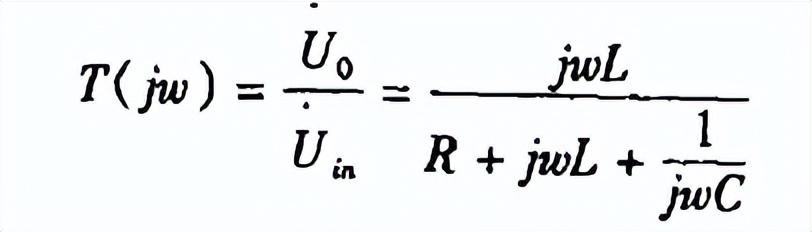
顯然，上述兩個數學表達式具有完全相同的函數形式，也就是說，如求出了該電路瞬態響應中的傳遞函數T(S)，而將傳遞函數T(S)中的變量S換成變量jω，便可求得傳輸系數T(jω)的數學表達式。反之，如求出了該電路穩態響應中的傳輸系數T(jω)，而將傳輸系數T(jω)中的變量jω換成變量S，便可求得傳遞函數T(S)的數學表達式。在實際工程中，由于對電路變量施行拉氏變換較為復雜，因此，在計算分析時，一般則先求出電路的傳輸系數T(jω)，然后，再通過變量替代求出該電路的傳遞函數T(S)。

綜上所述，極點不但對正弦穩態低頻截止頻率起主要作用，而且，對時間特性同樣也起主要作用。在利用極點分析電路頻響特性時，應注意決定低頻域截止頻率的主要是數值較大的極點頻率。

04、總結

放大電路的頻響分析由兩部分組成，一是瞬態響應分析部分，另一是穩態響應分析部分。兩部分的分析方法基本相同，而且，在分析中都與電路的極點值有關。在對電路進行瞬態響應分析時，是通過傳遞函數T(S)來表征電路傳輸情況的；而在對電路進行穩態響應分析時，是通過傳輸系數T(jw)來表征電路傳輸情況的，但二者間卻存在著密切的聯系。同時，截止頻率與極點頻率，在放大電路的頻響分析中起著重要的作用。

綜上對放大電路所作的頻響分析，這在放大電路的分析和設計中是非常重要的，它為放大電路的分析和設計提供了必要的理論分析方法。