基于綜合效率的壓電換能器評價方法的研究
在功率超聲領域,壓電換能器作為一種重要的“電-聲( 力)”轉換元件,其性能的優劣直接關系到整個功率超聲系統的工況性能及效率。大量的應用場景需要壓電換能器具備穩定的輸出特性以及較高的能量轉換效率,能夠在長期連續的大功率條件下可以穩定輸出超聲波能量。針對壓電換能器性能的評價方法,1995 年,顏忠余、林仲茂[1]從理論上分析了換能器的結構和材料參數對其性能指標的影響,以及不同外部負載條件下這些參數對換能器性能的影響,并提出正確設計的方法。2001 年,俞宏沛等[2]通過建立在小功率空載激勵與額定大功率有載激勵.只要使其振動幅度相等則換能器振動的動態疲勞及損傷程度是近似相等的原則之上,對換能器在空載的條件下激勵,使其振動幅度等于有載下的標準參數值,使換能器在較小的功率級下進行較大的振幅下長期激勵振動后通過評價有效機電耦合系數keff 和機械品質因數Qm 與初始值的變化量來衡量換能器損傷與否。2007 年,Riera E 等[3]通過搭建基于LabView 的大功率換能器測試平臺,監測大功率激勵條件下換能器端的功率、阻抗、相位、振幅、溫度等多參數的數據,對測試樣品換能器進行綜合數據分析和評價。
本文引用地址:http://www.104case.com/article/202303/444286.htm從上述內容不難看出,目前針對換能器性能的評價,國內研究者主要基于小信號等效參數的評價,尚缺乏大功率激勵時換能器綜合表觀參數與小信號等效參數的相關性研究,而國外研究者開展了換能器的多種參數的綜合評價,但其測試設備昂貴和精密,導致應用場景非常受限。本文基于上述研究,通過將換能器動態參量Neff與實際大功率激勵條件下換能器溫度變化表觀參數的相關性進行分析,研究小信號測量條件下的集總參數與實際大功率激勵條件下的換能器表觀參數的相關性,建立了一種簡便、高效的利用綜合效率評價換能器性能優劣的方法。
1 理論分析
1.1 換能器的力學等效系統
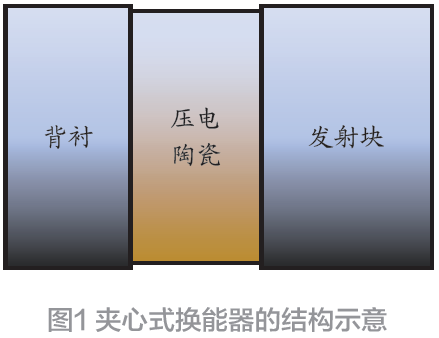
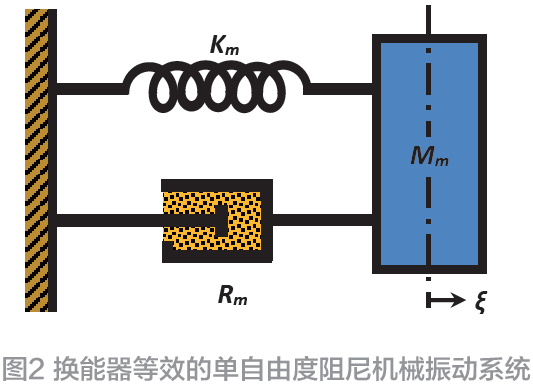
在功率超聲應用中,壓電換能器常采用“夾心式”結構(Sandwich constructions),圖1 為其典型結構示意,該結構一般由前輻射塊、壓電陶瓷以及后部背襯通過一定數值的預應力(預應力一般約為30 MPa)構成了一種力學串聯形式。圖2 為該結構換能器的力學等效模型。在不考慮負載的條件下,可以將其等效為如圖2所示的一個質量為Mm 的作單自由度運動的物體連接在彈性系數(剛度系數)為Km 的彈簧上所構成的“單自由度阻尼機械振動系統”,其中Rm 為彈簧做功時的阻尼,ξ 為質點的位移量。當質點Mm 被外力沿固定軸方向推離平衡點時,彈簧也同時產生拉伸形變,假設此時質點位移量ξ 未超出彈簧的彈性限度,根據胡克定律,其彈簧的彈力Fk與質點位移量ξ 存在以下關系[4]
![]()
通過式(1)可見,彈簧彈力Fk與質點位移量ξ 成正比,并根據牛頓第二定律,可以將式(1)改寫為
![]()
其中a 為質點Mm加速度,而加速度a即為位移量ξ的二階導數,因此可以將式(2)改寫為
![]()
以上是在未考慮阻尼Rm的情況,而將Rm引入后則可將式(3)改寫為
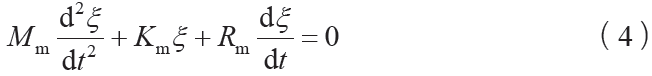
1.2 換能器的電學等效系統
考慮到求解電學問題的方法相較于力學更豐富和完善,在處理一些機械振動問題時可以利用相應變量物理意義的類比進行電學網絡等效[5]。因此,類比于力學系統的各變量的物理意義,可以將力學系統中的作為慣量形式存在的質量Mm等效為電感量Le,將儲能形式存在的彈簧彈力Km等效為電容量Ce,將機械阻尼Rm等效為電阻Re,并形成如圖3 所示的一個串聯形式的RLC等效電路。
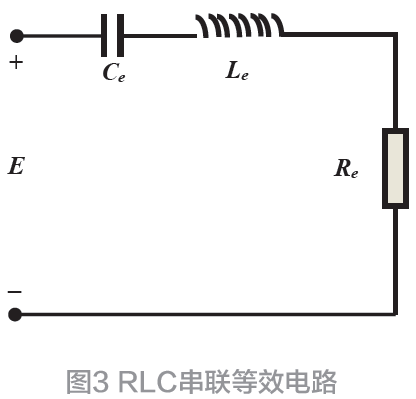
該電路中具有一個電場為E 的恒壓源,而各等效元件以串聯的形式連接構成了一個閉合回路,類比于力學系統,電場E即為力學系統中F在電學上的表現形式,而電流I則為力學系統中v在電學上的表現形式,則在閉合回路中的各等效元件具有以下的表現關系[4]
瞬態條件下等效電感
![]()
瞬態條件下等效電容

等效電阻
![]()
根據基爾霍夫第二定律可知,閉合回路中各元件上的電壓的代數和恒等于0,則可將上述等效電路表示為
![]()
以上是針對力學系統與電學系統的類比推導,可見兩個系統之間可以通過各元件在各自系統中所起的作用進行等效對應,這對于理解換能器的工作機制具有十分重要的意義,但對于功率超聲換能器而言,其電聲轉換效率的高低直接關系到換能器性能的優劣,特別是動態參量Neff可以較為全面的反映換能器結構、材料、工藝等多方面的性能指標[1]。其表達式為

其中,Qe為電學品質因素,Qm為機械品質因素,Keff為有效機電耦合系數,這些參量的表達式分別為[6]
![]()
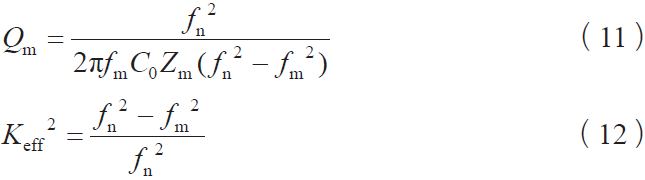
通過式(10)可以理解為Qe與介質損耗成倒數關系,并且其還有另一種表達式[7],即
![]()
其中,ω 為測試換能器靜態參量時的角頻率,C0為靜態電容,R為靜態條件時的損耗電阻,而式(11)、式(12)中的fn、fm、Zm分別表示為反諧振頻率和諧振頻率,以及最小阻抗值。而式(12)也可以通過換能器的電容比進行表達[7],即

綜合以上對換能器各集總參數的推導后可以獲得一個包含C0、tanδ、Zm、L1、C1這五個因素所構成的換能器等效模型,其中,C1為諧振狀態下的動態電容。并可以通過該模型得到與之對應的Neff 變化規律,經過歸一化后上述五個因素與Neff 的對應關系如圖4 所示。
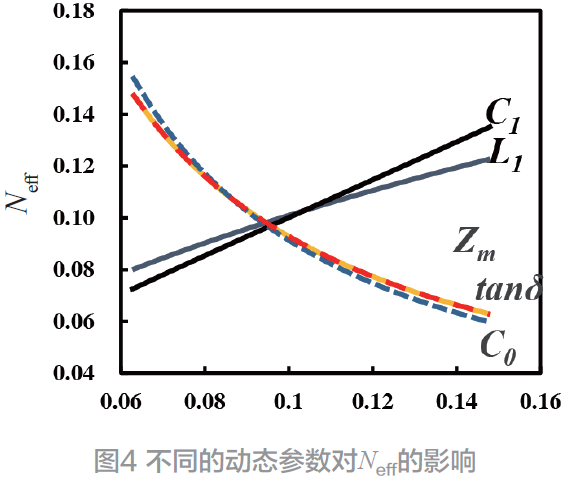
正如之前所推導的情況,通過圖4 可見,動態參數C1、L1對Neff起到了正面影響,而Zm、tanδ 及C0對Neff起到了負面影響,并且這三個因素影響程度相較于C1和L1更為顯著。
2 實驗過程
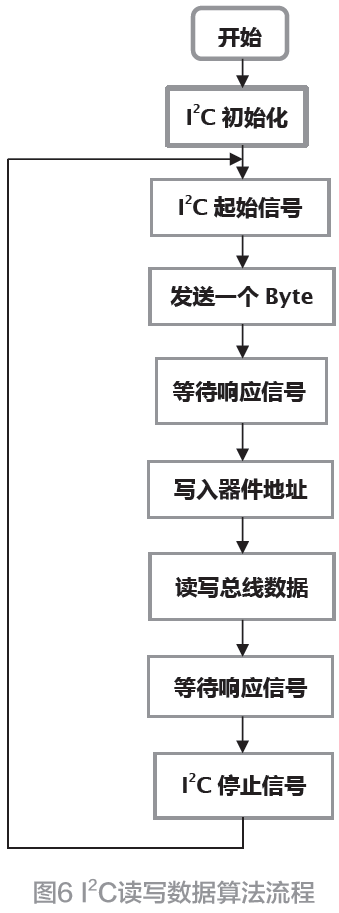
實驗目的主要為驗證換能器的小信號集總參數與實際大功率激勵條件的表觀的對應關系。實驗中分別選取了四種不同特性的PZT-8 壓電陶瓷材料,同時利用相同的換能器金屬結構部件和安裝工藝參數裝配形成如圖5、圖6 所示的具備了換能器、變幅桿以及工具頭的完整樣品,并先通過阻抗分析儀采集各樣品的參數后,按式(9)計算得出相應樣品的Neff數值。如圖7 所示,再利用大功率激勵信號源在無載條件(空氣中)下進行時長30 分鐘的大功率激勵,同時利用紅外熱成像儀記錄換能器各標志點溫度變化數據后求解出換能器積溫率(Rate of accumulated temperature)進行比較。其積溫率表達式為

其中,ΔT 表示換能器各標志點溫差,t表示為積溫時間。

圖5 實驗中所制作的換能器樣品

圖6 實驗中制作的完整樣品
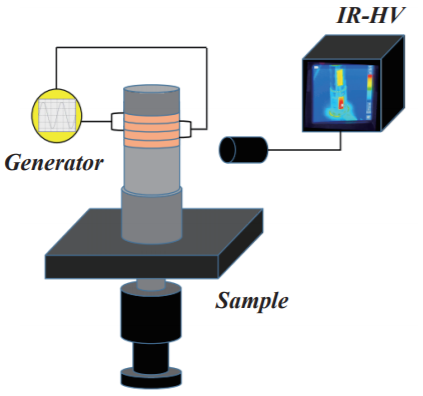
圖7 實驗中的測試系統示意圖
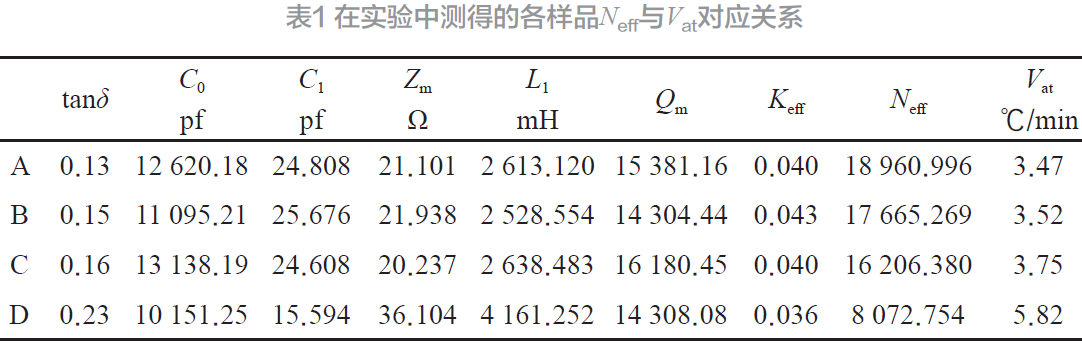
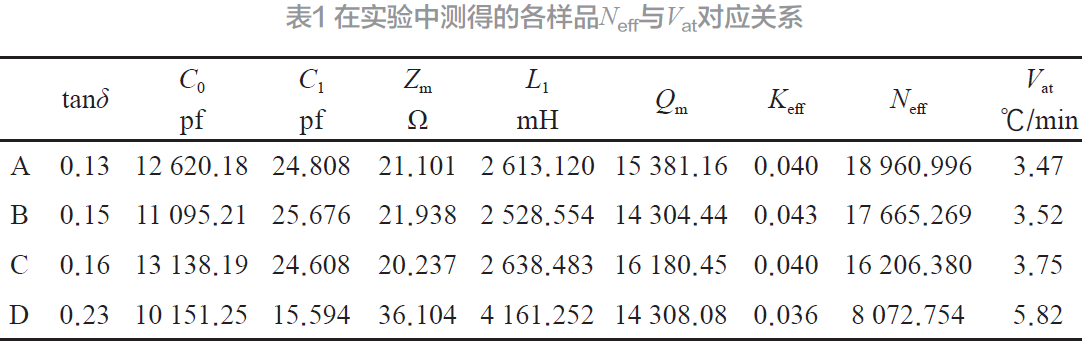
表1 顯示了利用上述方法獲得的各實驗樣品的相關電學等效參數和動態參量Neff以及與之對應的換能器積溫率Vat。通過表1 所示數據可見,Neff與Vat具有相關性聯系。
3 結果
通過上述實驗可以驗證換能器的綜合參量Neff與換能器在大功率激勵條件下的溫升呈現負相關性,隨著Neff的增高,換能器的整體的溫升速度也隨之降低。并且,就換能器的集總參數而言,明顯可見介質損耗tanδ與Neff之間呈現了明顯的直接相關性,而C0、C1、L1由于具備一定的關聯屬性,直接相關性不明顯。
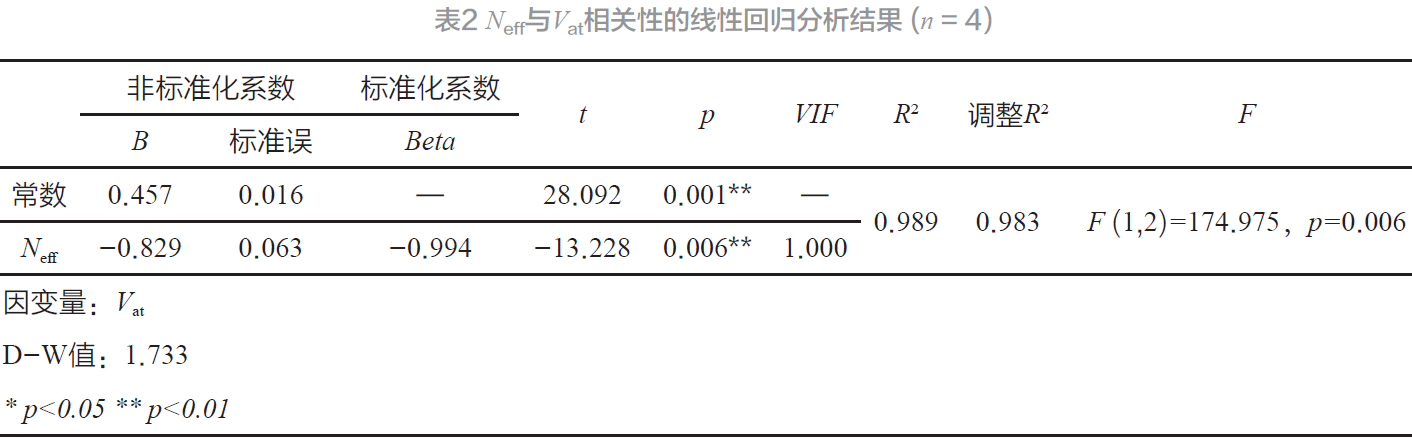
利用上述實驗結果,將Neff作為自變量,而將Vat作為因變量進行線性回歸分析[8],并從表2可以看出,模型公式為:Vat= 0.457-0.829×Neff,模型R方值為0.989,意味著Neff可以解釋Vat的98.9% 變化原因。對模型進行F 檢驗時發現模型通過F 檢驗(F = 174.975,p = 0.006<0.05), 也即說明Neff一定會對Vat產生影響關系, 最終具體分析可知:Neff的回歸系數值為-0.829(t = -13.228,p = 0.006<0.01),意味著Neff會對Vat產生顯著的負向影響關系。
4 討論
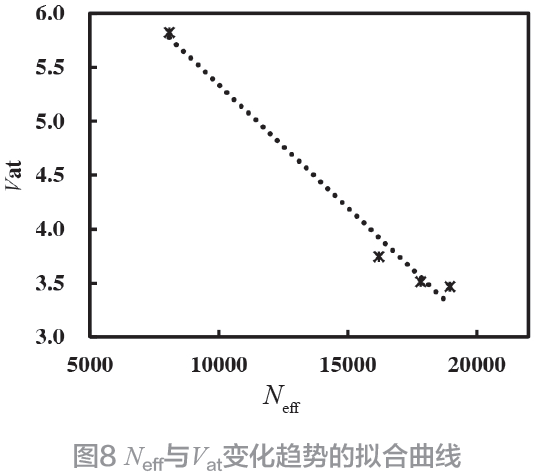
通過圖8 可以看到,對于一個完整的換能器而言,Neff與Vat呈現負相關性變化,即Neff數值越大,其所對應的Vat也越小。同時,利用數據的線性回歸分析結果也可知,Neff全部均會對Vat產生顯著的負向影響關系。當C1與C0的比值達到0.002時,并且C1與L1的比值達到0.01 時,換能器的整體Neff值將處于一個相對較高的水平,其溫升率則較低,換能器性能優異。而當換能器的上述比值分別低于0.0018 以及0.009時,換能器的Neff值偏低,溫升率則會偏高,換能器性能劣化趨勢顯著。綜上所述,通過對于換能器的集總參數等效模型與實驗的結果可見,換能器動態參量Neff可以較為全面地反映換能器的性能水平。并且可以發現,實際的大功率激勵后換能器的表觀積溫率Vat與動態參量Neff之間存在相關性聯系,通過直接獲取換能器Vat數據并結合Neff的比較可以簡便和迅速的評價換能器的性能水平的優劣。而通過等效模型分析并結合實驗結果可知,提高換能器的動態電感L1、動態電容C1并保持與靜態電容C0的一定比值,同時降低阻抗Zm和介質損耗tanδ,則可以獲得較高的動態參量Neff值。因此,基于本文的研究結果,特別是針對不同條件或狀態下,換能器的動態參數與靜態電容之間的比值與Neff 的對應性也將是后續研究的一個重要方向。
參考文獻:
[1] 顏忠余,林仲茂.夾心壓電換能器的優化設計─分析各參數對換能器性能的影響[J].聲學學報,1995(1):18-25.
[2] 俞宏沛,費國強,方玲.用壽命試驗來評估聲吶換能器[C].全國船舶儀器儀表二00一年學術會議.中國儀器儀表學會;中國造船工程學會,2001.
[3] Riera E , Juan A Gallego-Juárez, Blanco A , et al. Power characterization of ultrasonic piezoelectric transducers[C]. International Congress on Ultrasonics, ICU 2007. 2007.
[4] 杜功煥,朱哲民,龔秀芬.聲學基礎.2版[M].南京:南京大學出版社,2001.
[5] 滕舵,楊虎,李道江.水聲換能器基礎[M].西安:西北工業大學出版社,2016.
[6] 佚名.Piezoelectric Ceramics: Principles and Applications[J]. 2011.
[7] 林書玉.超聲換能器的原理及設計[M].北京:科學出版社,2004.
(本文來源于《電子產品世界》雜志2022年4月期)





評論