MBD應用于霍爾組件位置選定
在直流無刷馬達中,電磁仿真軟件不僅可設計馬達磁路本體,也可決定霍爾組件位置。本文采用Altair的電磁仿真軟件Flux進行馬達本體建模,在理論決定霍爾組件位置后提取磁通密度,再搭配系統開發平臺軟件建立六步方波電流驅動模型,完成符合物理定義的驅動與馬達整體模型。
應用model-based design(MBD)來設計各種不同產品已是目前主流,尤其在馬達設計時,電磁仿真軟件的導入已是不可或缺的工具。然而在直流無刷馬達此一產品中,電磁仿真軟件不僅可設計馬達磁路本體,也可決定霍爾組件(Hall Sensor)位置
直流無刷馬達
直流無刷馬達主要應用在風扇等開回路控制領域, 搭配霍爾組件(Hall Sensor)進行六步方波控制(圖1)。霍爾組件為偵測馬達轉子角度進而決定六步方波開關次序。當磁通密度超越固定值時,霍爾組件訊號由0->1,降低在固定值下時訊號由1->0。故而霍爾組件的位置影響馬達最終的扭力輸出,接著使用Altair公司的電磁仿真軟件Flux建立8極9槽馬達,藉由理論決定霍爾組件位置提曲磁通密度后建立六步方波。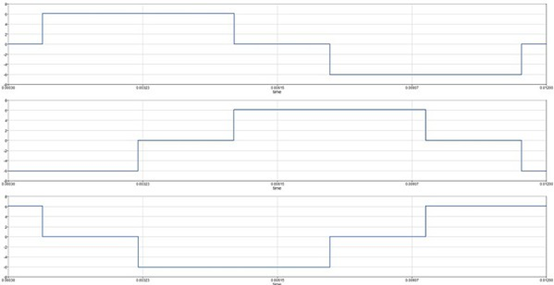
圖1 : 六步方波控制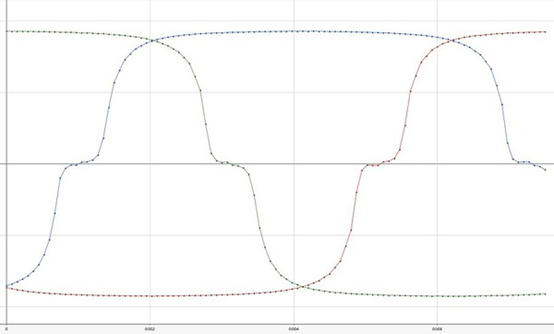
圖2 : 磁通量梯型波
表1 轉子角度與U相扭力關系
轉子角度 |
磁通量 |
電流 |
扭力 |
|
?? 0 |
0 |
0 |
0 |
|
30 |
1 |
1 |
1 |
|
90 |
1 |
1 |
1 |
|
150 |
1 |
1 |
1 |
|
180 |
0 |
0 |
0 |
表2 轉子角度與UVW相扭力關系
轉子角度 |
U扭力 |
V扭力 |
W扭力 |
總扭力 |
|
0~30 |
0 |
1 |
1 |
2 |
|
30~90 |
1 |
0 |
1 |
2 |
|
90~150 |
1 |
1 |
0 |
2 |
|
150~180 |
0 |
1 |
1 |
2 |
馬達扭力公式
馬達扭力公式,如下方程序1所示。扭力由馬達磁通量, 匝數與電流組成。匝數為純量,磁通與電流為向量,霍爾組件位置決定電流向量角度,進而影響馬達扭力輸出。直流無刷馬達的磁通波形為梯型波(設定峰值為1),如圖2所示,電流為六步方波(同樣峰值設定為1),磁通電流的夾角為90度,匝數同樣為1下馬達U相扭力如表1所示,將V相與W相扭力顯示在表2,可見馬達在不同轉子角度時UVW各相對扭力的貢獻,最終馬達總扭力為定值。
Torque = N * ? * Irms * cosθ (1)
其中
N為馬達匝數
?為馬達磁通量
Irms為馬達電流
θ為電流與磁通夾角
馬達與電流建模
在Altair的電磁仿真軟件Flux內建立 8極 9槽馬達模型(圖3),觀察U相磁通量波形如圖4所示的梯形波。輸入馬達的六步方波電流由Altair發行之系統開發平臺軟件Activate建立,由轉子角度與轉速計算得知六步方波的切換時序,確保電流與磁通量的夾角為90度,建立時間基準的六步方波電源,輸入Flux的馬達模塊,扭力曲線如圖5所示。
此模型的六步方波是由角度計算時間建立而成,并非實際的由霍爾組件切換狀況形成,與實際狀況仍有一段差距。因此接續將先采用理論計算UVW三相的霍爾組件位置,再于Flux內匯出這三個霍爾組件的磁通密度數值。將磁通密度數值匯入Activate軟件,設定切換開關狀態的數值后, 建立霍爾組件基準的六步方波并與時間基準的六步方波波形比較。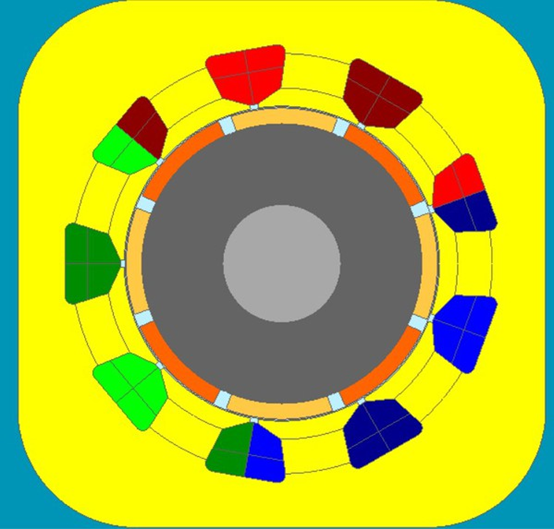
圖3 : 8 極 9槽馬達模型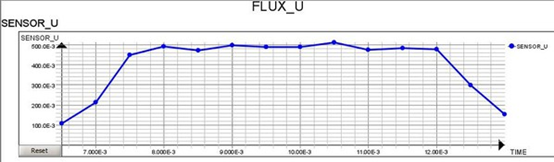
圖4 : U相磁通波形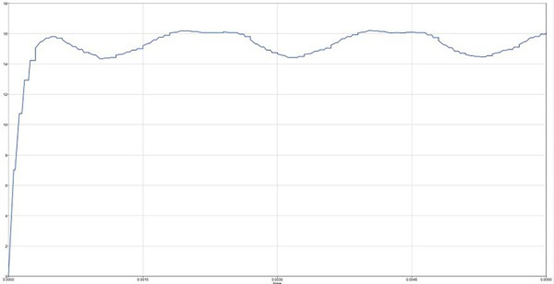
圖5 : 時間基準六步方波產生的馬達扭力曲線
霍爾組件位置
霍爾組件藉由偵測磁通密度的大小來決定狀態為0或1,三個組件狀態的改變建立如圖1的六步方波,此即為電流的電氣角度。電流與磁通量的夾角影響馬達扭力。所以霍爾組件的位置要從磁通量角度開始考慮,也就是馬達的定子齒部與轉子磁石位置。
要決定霍爾組件位置,需先決定代表的定子齒部與磁石,不同的槽極數狀況不同。范例馬達 為3相8極9槽設計,單一相位分配到3個定子,取正中央定子齒部為代表來計算磁通量與電流的角度。槽距(機械角)為40度。馬達極數為8極,極距(機械角)為45度,以U相來展開討論。
如圖3所示,可知 U相中央定子齒部的機械角為80度,正對深橘色的S磁石,此時的轉子角度為U相的d軸狀況。右 側NS的磁中性點機械角為57.5度。磁中性點到中央定子齒部角度為80-57.5=22.5度,電氣角度為22.5*4=90度。
方波為磁通量電氣角為30度時,訊號由0→1如圖6所示(以反電動勢代替磁通),換算回機械角的話,NS磁中性點要轉動30/4=7.5度,霍爾組件訊號由0→1,磁中性點原始角度為57.5度,轉7.5度后角度為57.5+7.5=65度,此即為理論上U相霍爾組件位置,狀態由0→1。
考慮繞線狀況得 知V相霍爾組件位置為U相加上機械角120度即為65+120=185,同理W相組件為V相位置加上120 度,185+120=305度。將此三個霍爾組件位置標示如圖7的X處所示。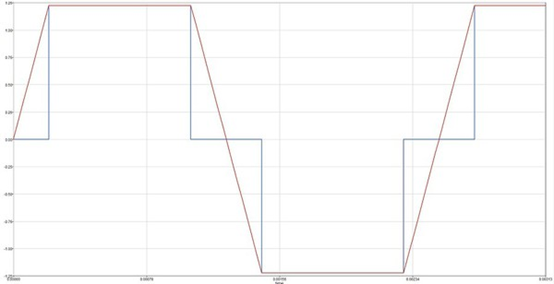
圖6 : 電流與反電動勢波形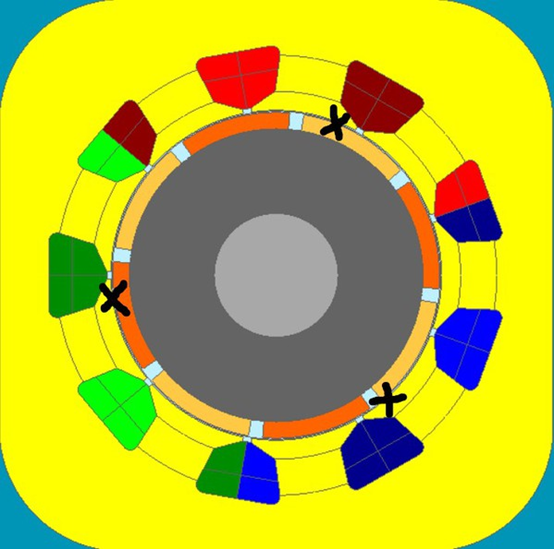
圖7 : 霍爾組件位置
霍爾訊號建立六步方波
將三個霍爾組件位置處的磁通密度數值從 Flux內匯出后,再于Activate內匯入(圖8),經過訊號處理設定切換0與1狀態的數值后,即是霍爾組件的狀態表(表3),進而完成建立六步方波模塊。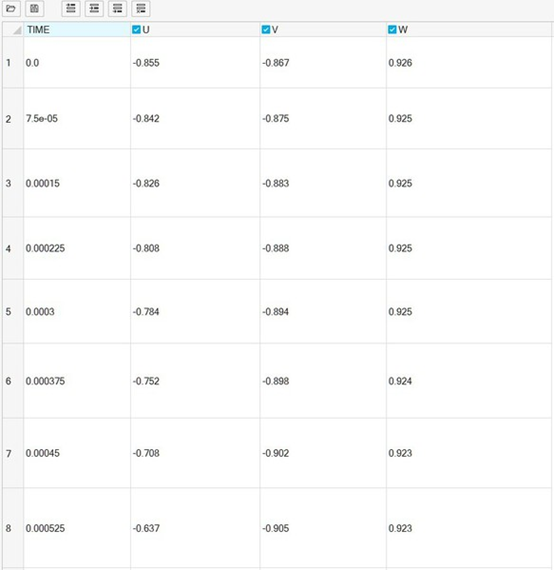
圖8 : 霍爾組件訊號匯入
接下來,比較時間基準的方波與霍爾組件基準的方波波形(圖9),可見兩種方式建立的六步方波非常相似,霍爾組件基準建立的六步方波與實際狀況相似,同時也吻合物理理論計算的結果。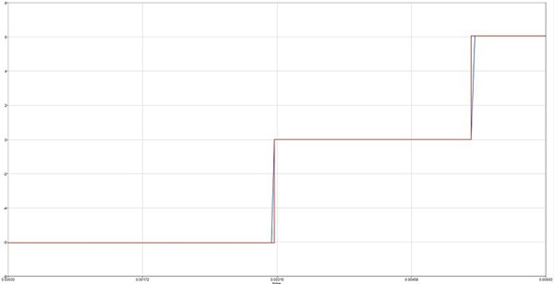
圖9 : 兩種六步方波波形比較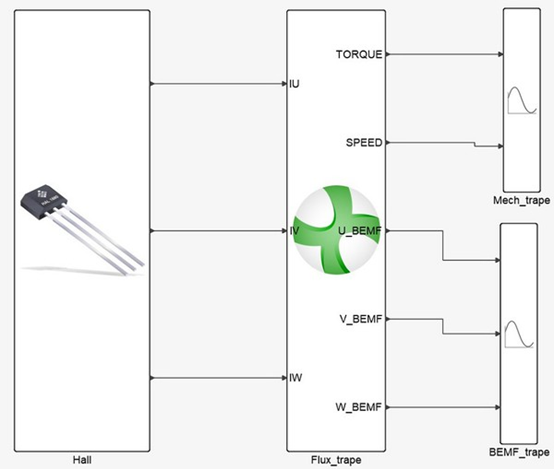
圖10 : 霍爾組件控制馬達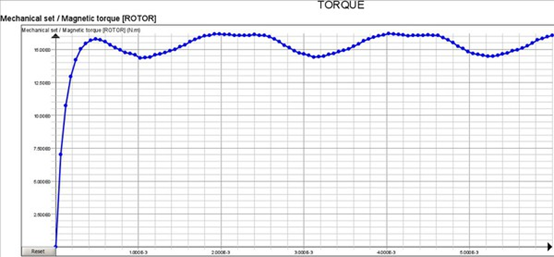
圖11 : 馬達扭力曲線
|
磁中性點角度 |
Hall ??U |
Hall ??V |
Hall ??W |
電氣角角度差 |
|
65~80 |
1 |
0 |
1 |
60 |
|
80~95 |
1 |
0 |
0 |
60 |
|
95~110 |
1 |
1 |
0 |
60 |
|
110~125 |
0 |
1 |
0 |
60 |
|
125~140 |
0 |
1 |
1 |
60 |
|
140~155 |
0 |
0 |
1 |
60 |
霍爾組件控制馬達
確認霍爾組件基準的方波與時間基準的方波相同后,由霍爾基準的方波電流取代原本時間基準的方波電流,輸入Flux當電流驅動,如圖10所示。在馬達為固定轉速轉動狀態之下,整個運作順序如下:
馬達轉子轉動改變霍爾組件位置磁通密度;
磁通密度變化改變霍爾組件狀態(0或1);
綜合三個霍爾組件狀態建立六步方波;
六步方波電流輸入馬達產生扭力。
整體模型,運作順序皆與實際系統相同。
此模型仿真的馬達扭力曲線如圖11所示,與時間基準的結果(圖5)相同,再次驗正霍爾模型的正確性;同時吻合理論的馬達總扭力為定值的結果。
結論
本文大費周章的從理論出發找出霍爾組件的位置,并以此建立霍爾組件基準的六步方波模型,其目的在于縮小模型與實物的差距,建立有物理理論根據的模型。此方法的好處是當處于開發階段試作品發生問題時,可藉此模型來一步步找出問題的根源,確認是霍爾組件損壞,或位置放置錯誤,還是訊號處理有問題?可將假設的原因建立在模型內,觀察仿真結果是否會產生跟實測時相同的問題?日積月累下,企業可累積研發單位的軟實力與設計經驗,不致受到人員變動造成能力流失的影響。
由于霍爾組件位置信息在初步設計時間即可獲得,試作品設計時就可采用確定的組件固定方式 ,不需采用可變動的固定方式,試作測試確認位置后再改變成確定固定方式,加速產品開發速度與節省開發費用。更進一步采用此MBD方式,設計初期就可以規范制程中需要控制的變異處,如反電動勢與霍爾訊號的角度,線圈繞線,以及轉向與霍爾位置三者之間的關系,都可藉由MBD的信息建立項目文件。
藉由使用Flux與Activate軟件,本文初步實現機與電訊號互傳的方式,Flux產生磁通密度匯入Activate,Activate藉由磁通密度建立六步方波再輸入Flux馬達產生扭力,日后更可完善驅動模型,逐漸達到機電合一雙向仿真的目標。
然而霍爾組件的位置會因不同馬達槽極數的設計而有所變化,模擬工具需搭配專業理論知識才能發揮出MBD的好處,逐步達到數字雙生(Digi Twins)的目標。
(本文作者陳志豪為佑謙科技電機顧問)



評論