推論先天八卦與整數樹

當前快速發展的信息化引發的信息爆炸，使計算機軟、硬件的處理能力已接近極限。原因是我們所使用的計算機是為處理線性數據設計的，對非線性數據一直是通過轉換來處理。隨著計算機要處理的非線性數據的增加，必然會使計算機數據處理能力不斷下降。

今后大范圍的云計算、物聯網，乃至智慧地球的應用中的無限天量非線性數據處理的需求，促使計算機軟、硬件在提高非線性數據的處理能力上創新。

計算機進行數據處理的基本操作是將數據按一定算法程序，在計算機系統內的不同存儲單元間移動。數據移動的速度決定計算機數據處理的能力。因此，數據存儲技術是提高計算機軟、硬件的數據處理能力的核心技術。又因，數據存儲技術的基礎是數據結構，發明或發現新的數據結構，將是提高數據存儲技術的探索方向。

北斗時空碼采用北京乾坤化物數字技術有限公司的自主知識產權的“IP地址結構樹的構建方法”發明專利建立的索引系統能夠快速提供無限天量編碼，就是在發現源于先天八卦的整數樹數據結構基礎上，做了進一步創新后實現的。

一、以往看先天八卦與數

先天八卦是中國寶貴的歷史文化遺產。相傳先天八卦是由中華民族的先祖伏羲畫的。由于沒有文字記錄，對先天八卦的來歷無從考證。但是，幾千年來，對先天八卦的含意，人們從各種學科角度進行了一代一代的不懈研究，得出了后天八卦、易經等許多富有哲理的深奧結果，有些推論至今還有很大影響。

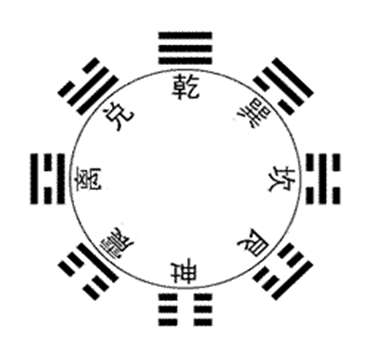
 圖1： 先天八卦圖

先天八卦是圖1圓圈外用陽爻“—”和陰爻“- -”兩種連和斷的橫線，以三層不同組合的八種卦的圖形排列的圓形圖案。圓圈內的文字是后人研究先天八卦賦給的每個卦的卦名。圓圈是為能明確分隔卦與卦名加畫的，沒有含意。

從數學角度看，古人對先天八卦產生的最有意義的推論是：太極生兩儀：陽儀、陰儀；兩儀生四象：太陽、少陰、少陽、太陰；四象生八卦：乾、兌、離、震、巽、坎、艮、坤；八卦生無窮。此推論是一種從哲學角度解說世界是從無到太極，從太極開始生兩儀，并按一分為二方式不斷分裂產生的。

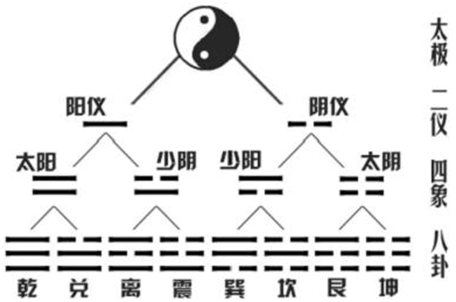
圖2：太極產生先天八卦圖

古人對太極產生的八卦又分別注上八個數字，即為：乾一、兌二、離三、震四、巽五、坎六、艮七、坤八。由此，指出八卦圖中相對應的兩卦：乾坤、兌艮、離坎、震巽卦的和都是九。

德國數學家萊布尼茲發明二進制后，有人將先天八卦中的陽爻“—”定義為1，將陰爻“- -”定義為0；然后將先天八卦的八個卦分別注上二進制，即：乾為0：000、兌為1：001、離為2：010、震:為3：011、巽4:100、坎5：101、艮6:110、坤為7：111。也指出用二進制定義八卦后，八卦圖中相對應兩卦：乾坤、兌艮、離坎、震巽卦的和都是7：111。

近代，數學家用a表示先天八卦中的陽爻“—”，用b代表陰爻“- -”，然后代入(a＋b)的n次自乘的牛頓二項式公式，準確推論出太極生八卦、八卦生無窮的每次生卦的數量和卦的組合狀態。經論證，可以看到先天八卦的生卦與二項式公式完全吻合，不盡讓人另眼看先天八卦深奧的數學含義。

二、另眼看先天八卦與數

用數字一至八表示先天八卦中的每個卦，還是用二進制000至111表示先天八卦中的每個卦都是人為的定義，不一定代表原畫卦者的初衷。數字0的出現和廣泛使用是在12世紀，因此，將先天八卦中的陰爻“- -”看做為0進行推論，不符合歷史實際。

由于用數字一至八或用二進制數000至111表示先天八卦中的每個卦，都是在人為的，或靜態的看先天八卦，不能將每個卦之間的客觀關系和每次生卦的動態生長關系表示出來。因此，在數學上一直沒能對先天八卦進行更深的推論。再加上一些古人推論八卦與觀測星象、預告未來等有關，但因其中許多推論與現代科學不符，越來越不被世人信服，反使先天八卦日益受到冷落。

世間的創新，首先是思路和方法的創新。以往對先天八卦的數學探討，都是先在主觀上定個假設，再進行推論，沒看到先天八卦的實質。即然畫出先天八卦的時代還沒有文字，不仿將爻的圖示簡單地進行直觀：將先天八卦中的陽爻“—”還看做1，將陰爻“- -”就看做2，再觀太極生八卦圖就會產生新的思路。

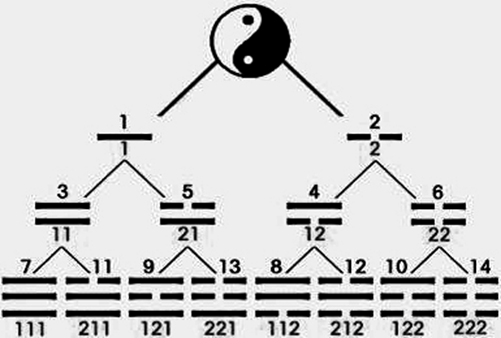圖3：另眼看太極生八卦圖

圖3與圖2是一樣的太極生八卦圖，只是將圖2中的二儀、四象和八卦的文字標識去掉，改注了數字。圖3中的二儀、四象和八卦的上部標的是十進制數，下部標識的是將二儀、四象和八卦的陽爻“—”替代為1，陰爻“- -”替代為2的對應一組數字表示符。從圖3中，可以看到用1和2標識陽爻和陰爻是非常直觀和清晰，也許更客觀地貼近畫先天八卦者的思想。圖4是用1和2對應標識陽爻和陰爻的先天八卦圖。

三、二的冪次方進制數

為進一步推論先天八卦中的數字關系，將圖3中每個二儀、四象和八卦的下部替代陽爻“—”為1，陰爻“- -”為2的對應一組數字表示符，以及圖4中對應各卦的由1和2組合的一組數字表示符，定義為是二的冪次方進制數。

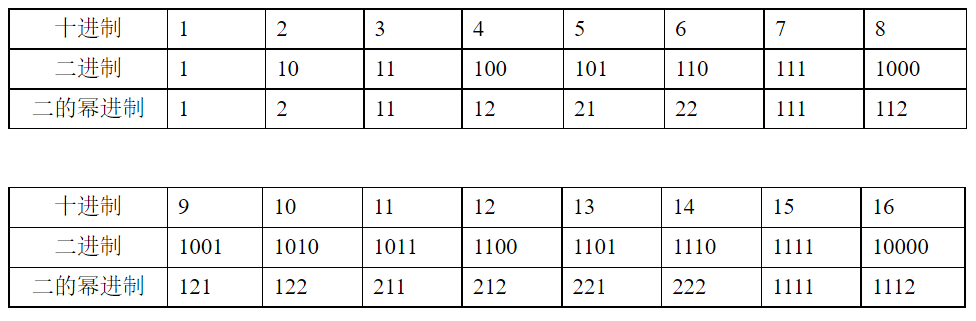
表1是十進制1至16與對應二進制、二的冪次方進制數對照表。 

表1：十進制1至16與對應二進制、二的冪次方進制數對照

二的冪次方進制數是一種新的計數方法，它由兩個基本數字符號1，2組成（也可以規定為0和1或A或B等）。二的冪次方進制數還有一個字符：0 （也可以規定為3或C等），用于表示第三種狀態，如：相等、起始、高阻態等。在二的冪次方進制數中，0不用于表示數，但做為正、負整數樹的起點（根）存在。如同太極，無形無質，無聲無臭；可是它有神有氣，有靈有顯，可以無中生有。

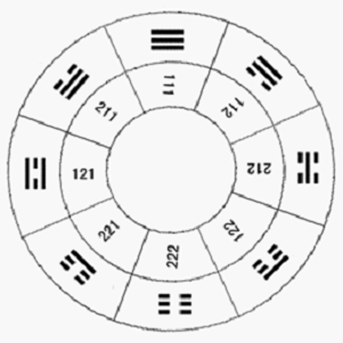
 圖4 ：用1和2對應標的先天八卦圖

二的冪次方進制數計數規律是滿二的冪次方值時向上位進一，且進位位恢復系數為1。為符合人們日常十進制運算習慣，我們將二的冪次方進制數中，用數字符號1直接表示整數1，用數字符號2直接表示整數2，可使這二個數字符號的表示與十進制的整數1和2相同。整數3以后的整數也用1或2兩數字符號表示。如：整數3將產生進位，用兩位數字符號11表示，整數4不產生進位，用兩位數字12表示，整數5產生進位，用2位數字21表示，整數6不產生進位，用兩位數字22表示，整數7產生兩次進位，用三位數字111表示……。由此可以看到：二的冪次方進制數對應N位整數Z的表示應為：

           Z= X(N)X(N-1) …X(N-N+3)X(N-N+2)X(N-N+1)X(N-N)

其中，X={1,2}，X數字符號，N={0,1,2…}, N是位數。

每個整數在二的冪次方進制數中僅表示出每位的數字符號，省略了每位對應的數位的權，即二的冪。這與十進制、二進制和十六進制等數字表示時省略數位的權一樣。^注1

圖3中的二儀、四象和八卦的上部標的十進制數就是每個二儀、四象和八卦的二的冪次方進制數對應的十進制數。圖5是用十進制數標識的先天八卦圖。

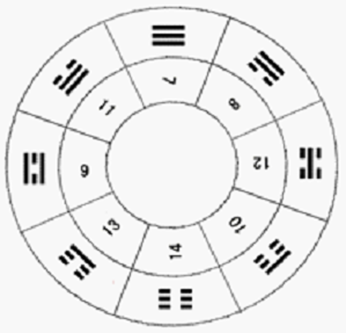 圖5：用十進制標識的先天八卦圖

從圖5中也可以看到用十進制表示先天八卦中各卦后，八卦圖中相對應兩卦：乾坤、兌艮、離坎、震巽卦的和都是十進制數21。還可以看到從乾卦逆時針的乾、兌、離、震四卦對應的十進制數7、11、9、13都是奇整數，從巽卦開始順時針的巽、坎、艮坤四卦對應的十進制數8、12、10、14都是偶整數。這是從先天八卦轉換出來的非常有創新意義的數據結構。

四、二的冪次方進制數標識八卦生無窮

二的冪次方進制數是將古人用陽爻“—”和陰爻“- -”兩個符號表述：無極生太極、太極生二儀、二儀生四象、四象生八卦、八卦生無窮的生變過程，用現代人習慣的用1代替陽爻“—”，用2代替陰爻“- -”后再次標識產生，與古人用爻表示是一一對應的。因此，二的冪次方進制數不是新發明，僅用新符號表示先前已存在的數據結構。

從圖2、圖3中可以看到太極生八卦圖是以太極為根的二叉樹。由太極生出兩個子結點：奇數結點和偶數結點 分別為二儀。用陽爻“—”表示奇數結點陽儀，用陰爻“- -”表示偶數結點陰儀。再生變，兩儀又做父結點，各生出兩節點分別為四象。再生變，四象又做父結點，各生出兩節點分別為八卦。然后再生變，八八生六十四卦，乃至可生出無窮。將此種結構的二叉樹，定義為整數二叉樹。圖6為古人的六十四卦圖。

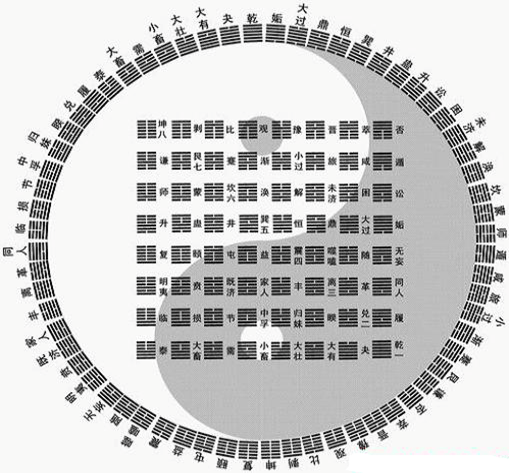
圖6：六十四卦圖

用1代替a，用2代替b，并且n=1、2、3……，展開二項式公式(a+b)ⁿ可得到如下結果：

(a+b)¹=(1+2)¹=1+2

(a+b)²=(1+2)²=(1+2) (1+2)=11+21+12+22

(a+b)³=(1+2)³=(1+2)²(1+2)=( 11+21+12+22) (1+2)

=111+211+121+221+112+212+122+222

…………

   將上述每次二項式公式展開得到的數，看做是二的冪次方進制數，將第1式展開數1、2擺在上層，再將后兩式展開數，依此按層向下排列如下：

用陽爻“—”和陰爻“- -”分別代替展開結果中各項的1和2。然后將替代后的每個爻的組合，按最左側爻在上，最右側爻在下的順序排，就可看到與圖3：古代太極生兩儀、兩儀生四象、四象生八卦相同圖。由此，可以證明二的冪次方進制數與先天八卦的對應關系。圖7是用二的冪次方進制數和對應十進制數表示的六十四卦圖。

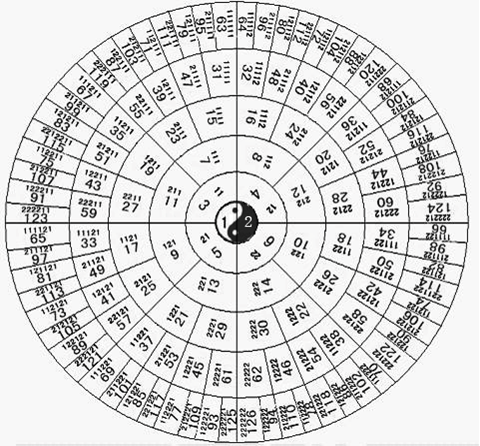
  圖7：用二的冪次方進制數和對應十進制數表示的六十四卦

將圖7最外層每個二的冪次方進制數與圖6中六十四卦所對應的每個卦相比較，可以看到都是一一對應相同的。只是用1或2表示，還是用陽爻“—”和陰爻“- -”表示的不同。

從圖7中的中心園的1和2到最外層圓的各二的冪次方進制數是按一生二的規則生變的，而且非常簡單。每個奇數子結點的二的冪次進制數是其父結點二的冪次方進制數前放置1產生，每個偶數數子結點的二的冪次進制數是其父結點二的冪次方進制數前放置2產生。這與用爻表示太極生二儀、二儀生四象、四象生八卦、八卦生無窮的生變過程：即每生變一次結果是在生變前的用爻表示的圖形上添畫一個陽爻“—”產生左邊（奇數）子圖形，添畫一個陰爻“- -”產生右邊（偶數）子圖形是完全一樣的。用二的冪次方進制數標識太極生八卦、八卦生無窮會更直觀。

引入二的冪次方進制數的更重要意義是，可以用數學計算與先天八卦生變過程對應的數據結構：整數二叉樹。

五、先天八卦揭示的整數二叉樹

將圖3太極生八卦圖中的太極用0代替，并將二儀、四象和八卦圖形去掉，再多生變一次（多顯示一層整數二叉樹），可得到圖8所示的整數二叉樹最頂的四層結點的數據結構。

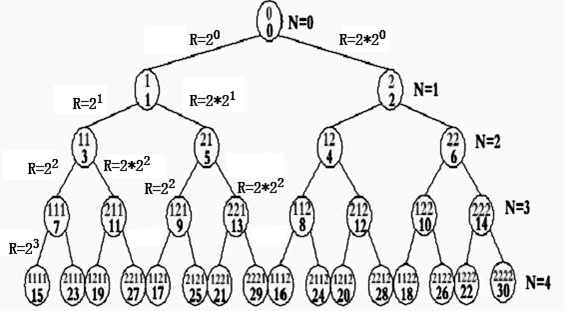
圖8：用二的冪次方進制數和十進制表示的四層整數二叉樹

圖8中圓圈為整數二叉樹的每個結點，圓圈內上部數字為用二的冪次方進制數表示出的整數的結點代碼，下部數字為與結點代碼對應的十進制整數。字母N表示整數樹的層數，字母R表示各父結點與子結點的差值。

整數二叉樹最頂的父結點是整數二叉數的根，其結點代碼和對應十進制數都為0。由根的父結點生長（生變）出二個子結點1和2結點，由此不斷生長，長成無限層的整數二叉樹。

整數二叉樹上每個子結點值的生長公式為M_N+1 = M_N + X*2^N，這是一個遞歸方程式，其中X={1,2}，X是數字符號，代表整數二叉樹的2個子結點數。N={0,1,2,…}, N是整數分布的層數，M_N 為第N層一個父結點的整數值，M_N+1 是要計算出的M_N的子結點整數值。當N=0時，M_N =0，它表示整數二叉樹的開始，對于N>0的任何一個M_N ，其子整數有并且必須有2個，分別為M_N+1 = M_N + 1*2^N，M_N+1 = M_N + 2*2^N。

從圖8中可以看到整數二叉樹有以1為父結點的全部各層結點都為奇數的子結點分叉樹和以2為父結點的全部各層結點都為偶數的子結點分叉樹。這是整數二叉樹數據結構的重要特點。理論上整數二叉樹還應有負奇數和負偶數兩個分叉樹，在此不做推論。

從整數二叉樹的圖8中可以明顯看到一些規律：

1、整數按奇數和偶數有規則地組成為兩個分叉樹。

2、每層的結點數為2^N個，N為層數。

3、每個父結點有兩個子結點：奇數子結點和偶數子結點。父結點與奇數子結點間的差值R= 2 ^N，與偶數子結點的差值R=2* 2 ^N，N為父結點的層數。

4、兩個子結點之間差值為父結點與奇數結點的差值R=2 ^N，N為父結點的層數。

5、每層各結點的二的冪進制數結點代碼的位數都等于該層的層數N。

6、每層各結點的二的冪進制數結點代碼值都等于該結點十進制整數值。

7、每層各結點的二的冪進制數結點代碼和對應十進制整數值的位置固定不變等等。

對整數二叉樹進行深入的研究，會對整數產生更多的認識和新的算法。支撐北斗時空碼的無限天量編碼可通過快速計算產生存儲地址的索引系統的核心技術，主要源自上述整數二叉樹的規律。

例如，要對整數28進行存取的操作，先將28通過計算轉換成二的冪次方進制數（注1）2212，實際2212已是28的存取地址碼。然后可采用多種方法可找出存取28的結點。方法一是通過2212可知28存取得結點在整數二叉樹的第4層，直接到該層用某種算法去找。方法二是從28算出的二的冪次方進制數2212的最右側（最低位）數開始，逐位判別是1還是2，決定從根結點0開始判別位是1向左下行至下一層結點，是2向右下行至下一層結點，以此類推，一個整數計算得出幾位二的冪次方進制數就判轉幾次，最后到達的結點必是要找的結點。

繼續以2212為例，從根結點開始，因2212最右數為2，要先右下行一層，2212的右數第二數為1，再左下行一層，然后2212右數第3和第4數都為2，再連續右下行兩層，就到整數28要存取的結點（圖8中第四層的從左數第12個結點），此結點永遠是存取28這一整數的結點。

客觀存在的事實是：無論多大和多小的整數，在整數二叉樹上都固定有自己對應的結點。此結點的地址碼就是該整數的二的冪次方進制數。

六、整數無窮叉樹與無窮冪次方進制數

數學源于自然數的計數。數學的發展，在自然數的基礎上陸續派生出整數、實數、虛數等等。整數是目前用的最多的數。整數是公差為1的整數等差數列，也可看做整數一叉樹。如圖9所示：

圖9：整數一叉樹    

 整數一叉樹的層數N=0、1、2、3、4……，每層結點數為1^N，都是1個。各結點的差值R=1^N，也都為1。子結點的生長公式為M_N+1 = M_N + X*1^N。式中M_N為M_N+1的父結點，N=0時M_N為0，X為子結點數，此處為1。對于N>0的任何一個M_N ，其子結點有并且必須有1個。

 圖10是用十進制數表示的整數二叉樹。圖中N=3層用深色底標出的八個結點中的數，就是先天八卦排列的八個卦對應的十進制數。從圖中可以清楚地看到先天八卦在整數二叉樹上的位置。

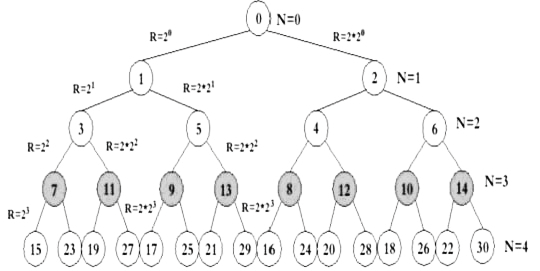
圖10：用十進制數表示的整數二叉樹

整數二叉樹用于數據存取地址索引的方法，在數據量少時，顯不出優勢。但是在數據量很大時索引速度還不會很快。這是因為，N層整數二叉樹上的結點個數Z的計算公式為：Z=2*2^N -1。如果事先知道要處理的最大整數值時，用此公式可算出至少需要多少層的整數二叉樹。當整數二叉樹層過多時，用在整數二叉樹的查找方法，查找整數Z的速度會較慢。

可以推論：整數以一叉樹、二叉樹數據結構排列外，同樣可以按多叉數，乃至無窮叉樹排列，而且各個叉樹的特點和規律相同。圖11是整數三叉樹的上三層各結點排列圖。

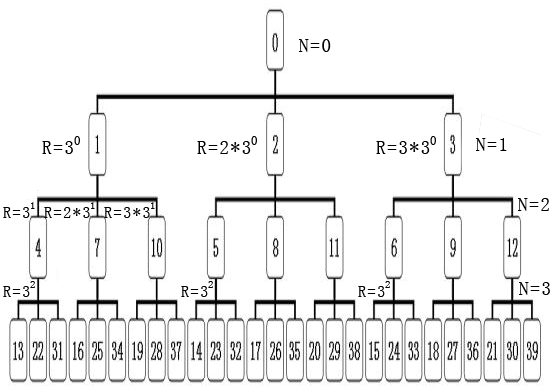
圖11：整數三叉樹的上三層各結點排列

整數三叉樹上每個子結點值的生長公式為M_N+1 = M_N + X*3^N，其中X={1,2，3}，X是數字符號，代表整數三叉樹的3個子結點數。N={0,1,2,…}, N是整數分布的層數，M_N 為第N層一個父結點的整數值，M_N+1 是要計算出的M_N的子結點整數值。當N=0時，M_N =0，它表示整數三叉樹的開始，對于N>0的任何一個M_N ，其子結點有并且必須有3個，分別為M_N+1 = M_N + 1*3^N，M_N+1 = M_N + 2*3^N，M_N+1 = M_N + 3*3^N。

圖12是整數四叉樹的上三層各結點排列圖。

整數四叉樹上每個子結點值的生長公式為M_N+1 = M_N + X*4^N，其中X={1,2，3，4}，X是數字符號，代表整數三叉樹的4個子結點數。N={0,1,2,…}, N是整數分布的層數，M_N 為第N層一個父結點的整數值，M_N+1 是要計算出的M_N的子結點整數值。當N=0時，M_N =0，它表示整數四叉樹的開始，對于N>0的任何一個M_N ，其子結點有并且必須有4個，分別為M_N+1 = M_N + 1*4^N，M_N+1 = M_N + 2*4^N，M_N+1 = M_N + 3*4^N，M_N+1 = M_N + 4*4^N。

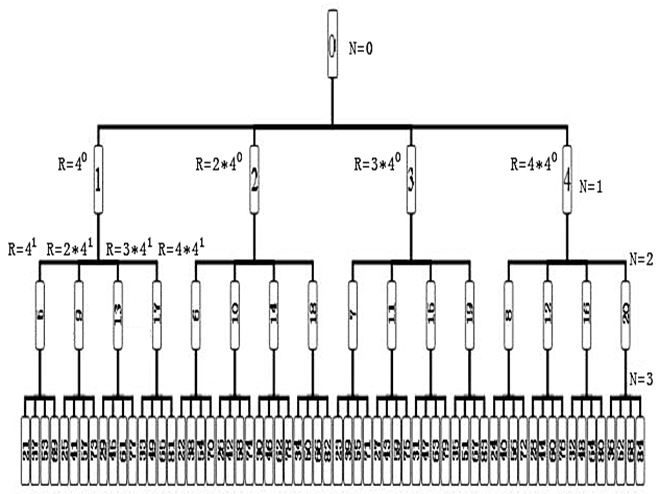
圖12：整數四叉樹的上三層各結點排列

    以整數三叉樹和四叉樹產生為例，可以得到整數五叉樹、六叉樹……Y叉樹，直至無窮叉樹。

同樣以二的冪次方進制數引入方式，可以引入三的冪次方進制數、四的冪次方進制數……Y的冪次方進制數，直至無窮的冪次方進制數。

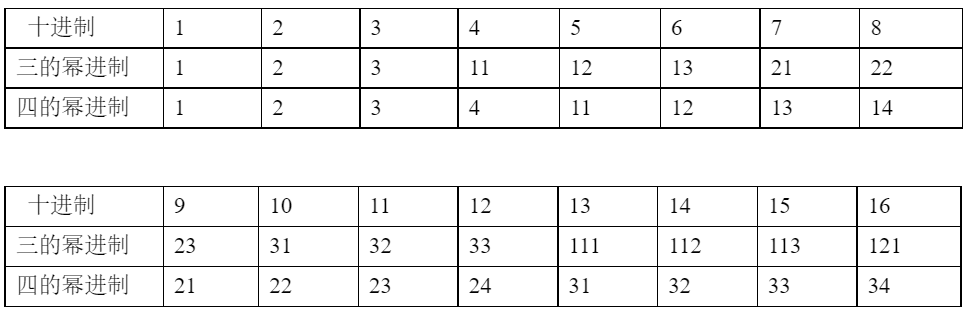
表2是十進制1至16與對應三的冪次方進制數和四的冪次方進制數對照表。      

表2：十進制1至16與對應三和四的冪次方進制數對照

七、結論

一、由先天八卦的生變過程推導出的整數二叉樹是整數的一種數據結構。

二、除整數二叉樹外還有從一叉樹到無窮叉樹，統稱整數樹或整數森林。

三、整數森林中任何一個Y叉樹都有無窮多個結點。

四、任何一個整數Y叉樹第N層及其上面各層的結點總數Z=2*Y^N -1。

五、任何一個整數Y叉樹都有一個與其所有結點位置相對應的Y的冪次方進制數。

六、任何一個整數Y叉樹上每個子結點值的生長公式為M_N+1 = M_N + X*Y^N，其中X={1,2，3……Y}，X是數字符號，代表整數Y叉樹的Y個子結點數。N={0,1,2,…}, N是整數分布的層數，M_N 為第N層一個父結點的整數值，M_N+1 是要計算出的M_N的子結點整數值。當N=0時，M_N =0，它表示整數Y叉樹的開始，對于N>0的任何一個M_N ，其子整數有并且必須有一個，分別為M_N+1 = M_N + 1*Y^N，M_N+1 = M_N + 2*Y^N……M_N+1 = M_N + Y*Y^N。

七、任何一個整數Y叉樹上每層的結點數為Y^N個，N為層數。

八、任何一個整數Y叉樹上每個父結點有Y個子結點。父結點與第1子結點間的差值R= Y ^N，與第2子結點的差值R=2* Y^N，……與第Y個子結點的差值R=Y* Y ^N， N為父結點的層數。

 九、任何一個整數Y叉樹上兩個子結點之間差值為父結點與第1子結點的差值R=Y ^N，N為父結點的層數。

十、任何一個整數Y叉樹上每層各結點的Y的冪進制數結點代碼的位數都等于該層的層數N。

十一、任何一個整數Y叉樹上每層各結點的Y的冪進制數結點代碼值都等于該結點對應十進制整數值。

十二、任何一個整數Y叉樹上每層各結點的Y的冪進制數結點代碼和對應十進制整數值的位置固定不變等等。

不斷研究和應用整數無窮叉樹的特性和規律，選用適合的某一整數多叉樹，可以對大數據、無窮天量數據進行快速管理。

幾千年來，人類對整數一叉樹的研究中，逐步建立了現代數學。一葉先天八卦，揭示整數森林。邁入整數森林，能否尋找到未來數學寶藏，還需更多人去探索。

注1：在網上可查閱“用整數樹的研究成果  探索軟件的創新發展”一文。