基于幾何優化的激光打標路徑孵化算法

摘 要：本文運用幾何優化、蒙特卡羅、路徑優化等理論方法，綜合運用MATLAB、EVIEWS和SPSS等軟件進行計算，從而構建了激光打標孵化模型。對于鋸齒形平行影線，首先分析圖形特征，將圖形劃分為易于處理的點集，對點集進行處理，從點集的最低點到最高點遞增，計算各層與點集的組成曲線的交點，連接相同高度的交點，最后整合成一個點集并繪制圖形。收集輪廓線所有點的坐標，對于其中一個點，使用不規則多邊形等距縮減公式計算平移和縮減后的坐標。收集所有點的平移坐標，形成新的點集，然后遞歸該點集，逐步提出下一個點集，直到不能再遞歸為止。

關鍵詞：幾何優化；路徑優化；MATLAB；激光打標

0 引言

激光打標是一種非接觸式打標方法。高能激光束聚焦在材料表面，快速蒸發材料并形成凹坑。當激光束在材料表面有規律地移動時，激光同時受到控制。關閉后，激光束會在材料表面加工成特定的圖案。與傳統的電化學和機械打標方法相比，它具有無污染、高速、高質量、無耗材等優點。國內激光打標經歷了大幅面、轉鏡、振鏡等時代。現在主要的工作方式可以分為掩模打標、陣列打標和掃描打標。掃描打標是通過計算機平移目標模具表面的 XY 坐標，從而改變激光束到達工件的位置。目前國內主要的研究方向是通過不同的硬件與計算機相結合來增加打標的準確性和效率，但是對提高計算機提供的 XY 坐標的精度和效率的研究還比較淺，本文旨在分析不同平面圖形、不同縮進邊距和影線間距、不同影線類型下的不同方案的效率，以不同算法所需的標記時間為考慮因素，對這一問題進行研究。

1 完全平面圖形

完全平面圖形為實心平面圖形，內部無凹槽，平面內部連續。在完整的平面圖形下，鋸齒形平行影線根據同一高度的圖形特征將圖形分為 7 個區域。在高度 h 的 條件下求 y = h 與這部分曲線的交點，連接兩個交點，平移 h 線，對所有切線都可用。根據輪廓形平行影線，先采集點集并計算下一級的點集，然后對點集進行處理并歸入下一級母集，最后得到所有輪廓線的點集。

1.1 全平面圖形鋸齒平行影線模型

1.1.1 模型原理

若連接輪廓點集內兩點的直線與目標直線相交，則兩點的高度與目標切線的高度差的乘積為負。使用這兩個點建立一個方程來求解目標切線高度處的交點。與切線高度相連的兩點是目標切線。分割后，同一分割線只能與該部分有兩個交點。

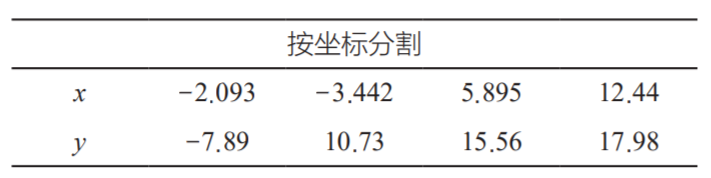
表1 各點的劃分基點(單位：mm)

1.1.2 模型建立

圖形劃分后，依次計算各部分。hmax 和 hmin 分別取該部分的最大值和最小值，d 為縮進距離。

最后，用 MATLAB 計算公式得，當縮進線和孵化線之間的距離為 1 mm 時如圖 1(a), 此時激光通過的總長度為 196.4336 mm，切線為 52 條線，算法耗時 0.0623 秒。

當縮進線和孵化線之間的距離為 0.1 mm 時如圖 1(b)、1(c), 此時激光路徑長度為 989.5264 mm，切線共 526 條，算法耗時 0.3591 秒 , 兩者耗時比為 5.764。

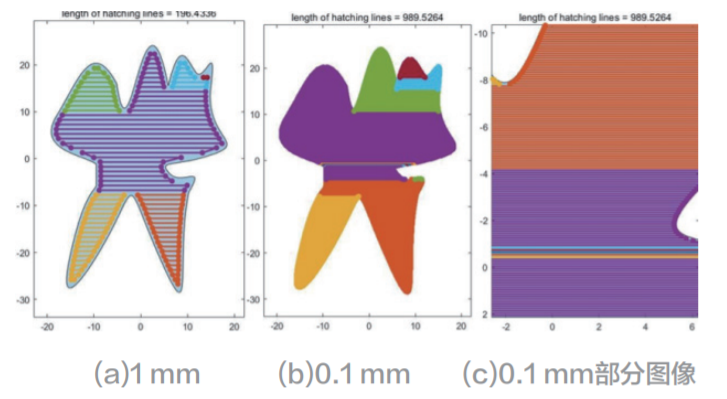
圖 1 不同距離切線圖形輪廓線平行影線模型

1.2.1 模型原理

利用不規則多邊形等間距約簡算法可以計算出點集對應的約簡點集。既然是一個完整平面圖形的計算，那么只會有一個點集形成的曲線自相交的錯誤結果。判斷i，i +1 點和 d，j +1 點是否相交如圖 2，若相交則去掉 i到 j 的點，以避免誤差。

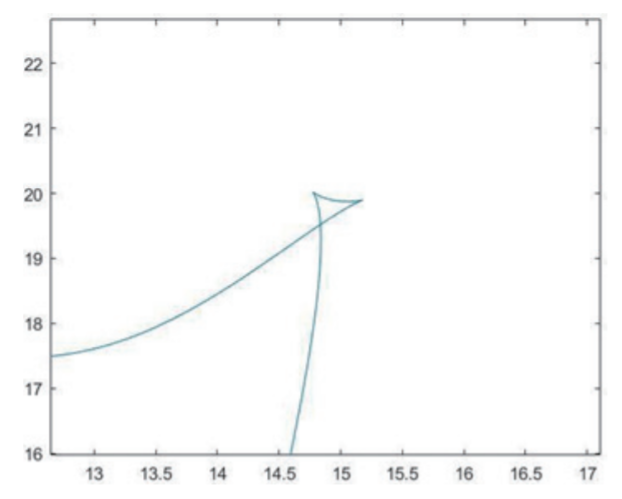
圖2 相交誤差

1.2.2 模型建立

圖3 不規則多邊形等距縮減算法

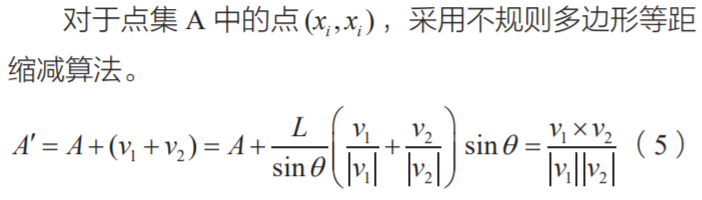
在有相交誤差的情況下，點集中的所有點形成 n 條 線段。用第 i +1 和第 n 條線段測試第 i 條線段。若第 i條線段和第 j 條線段 ( j > i ) 滿足以下四條中的一條：

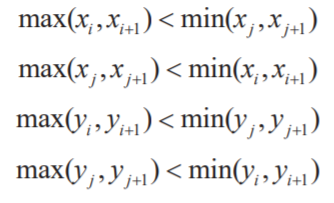
則進行測試的第二步，利用矢量積的規則，例如：如果 AB 和 CD 相交，那么

最后，通過 MATLAB 計算公式得，當縮進線和孵化線之間的距離為 1 mm 時：激光總光程 896.8205 mm，總圈數 9 圈，算法耗時 0.4624 秒。當縮進線與孵化線之間的距離為 0.1 mm 時，由于圖像過密僅顯示部分內容：激光總長 10 017 mm，總圈數 86 圈，算法耗時 3.6158 秒。到目前為止，兩者在該條件下的耗時比為 7.8196。

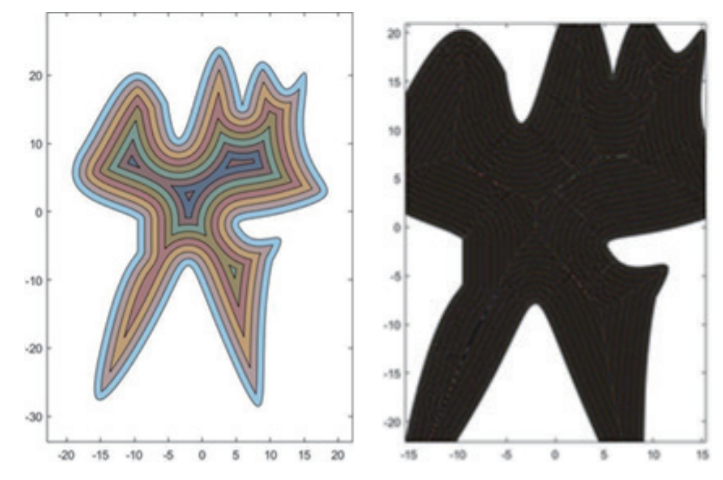
圖4 不同距離切線圖

2 嵌套平面圖形

嵌套平面圖形是空心平面圖形的一部分，溝槽內部還有其他平面圖形，平面不是處處連續的。嵌套平面圖形和完全平面圖形對于鋸齒形平行影線，只是在劃分區域上有所不同，但對于具有平行輪廓線的影線，這增加了內部空心圖形向外擴展的可能性。展開時，展開線和收縮線相交，兩條線相交點之間的線段消失，點集可以單獨討論。當兩者相交時，可以消去兩點之間的所有點得到結果，對于鋸齒平行影線，重新定義區分區域。

表2 各點的劃分基點（單位：mm）

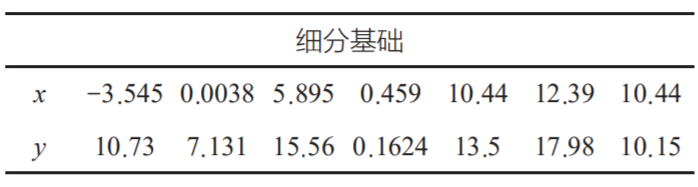
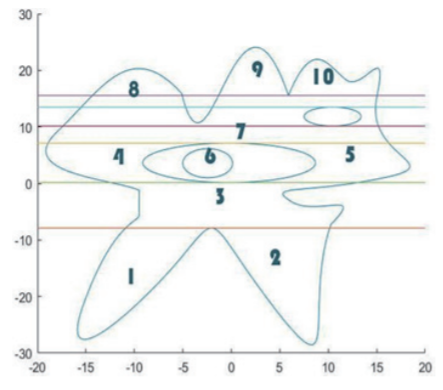
圖5 圖形分割

使用模型 1 重新劃分計算可以得到結果。當收縮余量與影線之間的距離為 1 mm 時，此時激光路徑長度為 189.0599 mm，總行數為 52，算法耗時 0.0865 秒，如圖 6(a) 部分圖像。

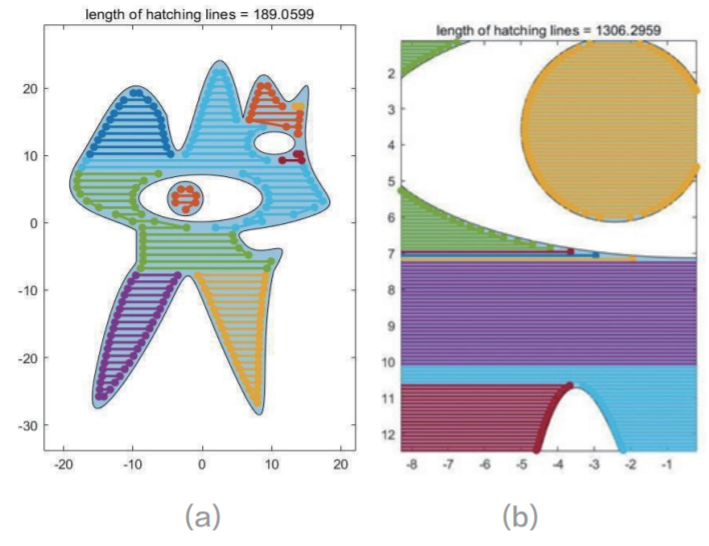
圖6 不同距離切線圖

當距離為 0.1 mm 時，激光器的總長度為 1 306.3 mm?，總行數為 526。該算法需要 0.4650 秒，兩種算法的耗時比為 5.3757。

對于輪廓形狀的平行影線，使用模型 2 的逆計算：

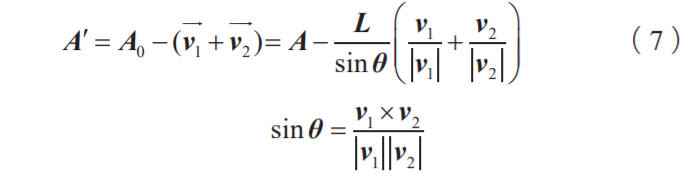
得到具有擴展嵌入邊界的點集 B。然后比較 A 中的第 i 條線段和 B 中的第 j 條線段，如果滿足求交公式，則記錄交點。因為交點總是成對出現，所以可以通過消除同時出現的兩個交點之間的點集來求解得到膨脹線和收縮線相交點，結果如圖 7。當收縮邊緣和陰影線之間的距離為 1 mm 時。此時激光路徑總長度為 773.0452 mm，匝數為 6，算法耗時 0.3935 秒。當收縮邊距和陰影線之間的距離為 0.1 mm 時。此時激光路徑長度為 9060.1 mm，總圈數為 60，算法耗時 2.9316。算法耗時比為 7.4501。

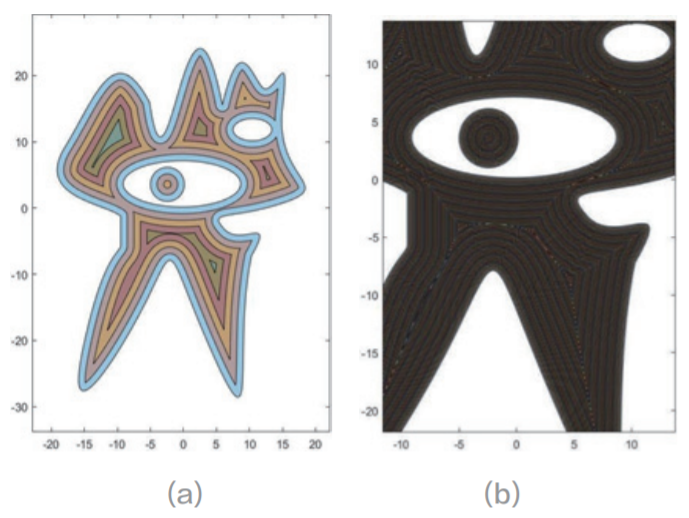
圖7 不同距離切線圖

3 模型推廣與優化

用 MATLAB 求解 t 隨 d 的變化曲線，當采用鋸齒形平行影線時，算法耗時受影線間距變化的影響如圖 8 所示。

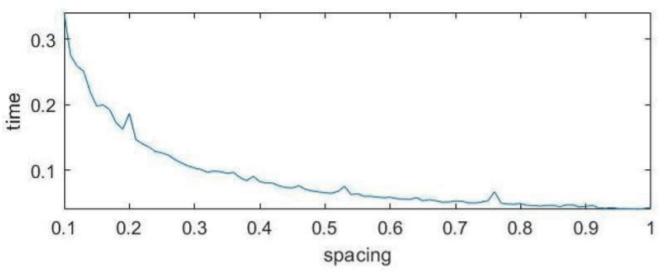
圖8

當采用輪廓形平行影線時，耗時的算法受影線間距變化的影響如圖 9 所示。

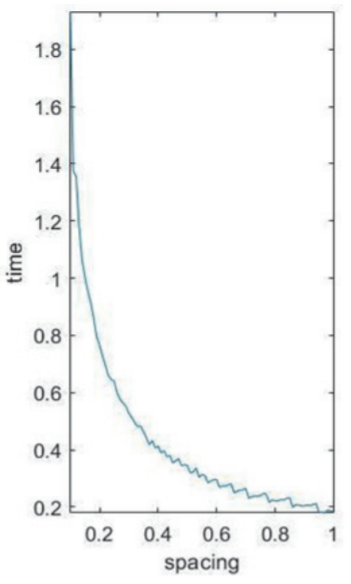
圖9

由此可知，當采用鋸齒形平行影線，且內邊距與影線的距離約為 0.5 mm 時，在保證算法效率的同時，可以盡可能地保證標記區域。求等高線平行影線時，由于是用無數的點集來模擬曲線，所以會有離散度小帶來的誤差。可以用逼近曲線來模擬點集所形成的曲線，然后用曲線來計算等距縮減線：

得到新的逼近曲線，然后用逼近曲線遞歸，最后得到所有等距線。

4 結語

本文對提高孵化效率的研究，可以大大提高日常激光打標的工作效率和速度。激光打標孵化算法的研究對于工業應用中生產效率的提高也起到了一定的作用，因為激光打標會產生大量的等高線數據，如何處理這些數據，提高孵化效率，這就是本研究的意義所在。

鋸齒形平行陰影有助于提供圖像定位問題的良好示例，例如激光標記和像素排列。模型 1 可以提供像素定位，這可以為計算機視覺的發展提供一個實用的算法，也可以為量子定位科學技術的其他需求提供一個研究方向。

模型 2 可以為一些科學軟件提供升級解決方案。在一些繪制圖形的工程軟件中，經常使用閉合線收縮。該模型可以為此提供更準確的閉合線收縮方案，保證工程圖紙的準確性。

參考文獻：

[1]?黃楨翔,王祥.建造導向的復雜空間結構拓撲幾何優化研究[J].建筑學報,2022(04):28-35.

[2]?吳瑞溢,李蕙萱.激光打標路徑孵化算法研究[J].哈爾濱師范大學自然科學學報,2021,37(05):62-67.

[3]?許晨昱,陳永明.應用于新型激光打標機的視覺標定算法[J].機電技術,2021(04):28-31.

[4]?彭川來.基于兩步法紋理映射的曲面零件激光打標技術研究[J].山西大同大學學報(自然科學版),2021,37(04):14-16.

(注：本文轉載自《電子產品世界》雜志2022年10月期)