帶漏電感的反激式轉換器平均模型

在本文第一部分，我們已說明了由漏電感帶來的開關效應：有效占空比的減少，帶來在主電源開關關斷后次級二極管導通時間的延長和次級端電流的延遲。因此，輸出電壓低于原來的公式預測，在RCD鉗位網絡中的功率耗散增加。鑒于漏電感對工作波形的影響，研究其對反激式轉換器小信號響應的影響是有趣的。但在我們進行小信號分析前，需要一個好的平均模型。

負載階躍響應

第一部分介紹的逐周期模型如圖1所示，現在包括一個可變負載。在這仿真中，負載范圍將從8至6 不等，跨度為10 μs，同時記錄輸出。轉換器運行在開環配置，我們會將漏電感從1 μH增加至50 μH，而其它工作參數保持不變(占空比40%)。

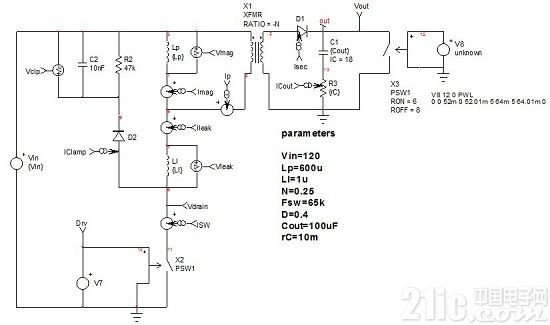
圖1：這開環簡化的反激式轉換器將讓我們探索由漏電感帶來的影響

我們已采集圖2中不同漏電感的輸出電壓。垂直刻度是每等分620 mV，對每一波形都相同，但偏移量有所改變以讓所有曲線進入圖中。第一個注釋涉及到振鈴。在幾乎沒有漏電感(1 μH)時，響應振鈴和阻尼很輕。但負載電流的步幅不影響輸出電壓。隨著漏電感增加，振鈴開始減弱，振蕩迅速停止，這時lleak = 50 μH。然而，漏電感越大，輸出電壓越低(從近20 V至17.6 V)，靜態電壓下降幅度越大：近0 V時無漏電感，達400 mV時漏電感最大。從這快速仿真中，我們可觀察到漏電感減弱瞬態響應，影響穩態輸出電壓(如第一部分所預測)，也會降低輸出阻抗。為探索漏電感對頻率響應的影響，我們需要一個大信號模型然后線性化以給出轉換器的小信號表達式。從這小信號模型中，我們應該能分析表達受漏電感影響的反激式轉換器的控制-輸出傳遞函數。

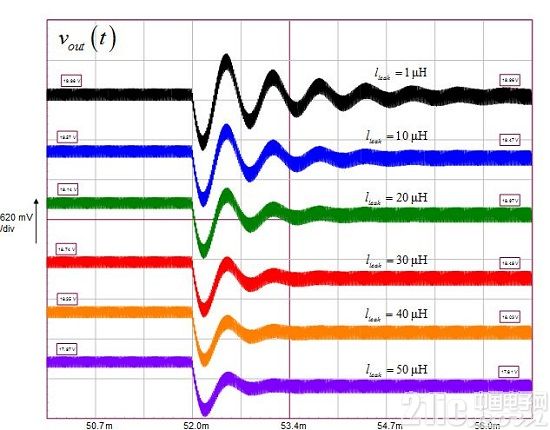
圖2：不同的漏電感影響開環反激式轉換器的幾個參數

大信號模型

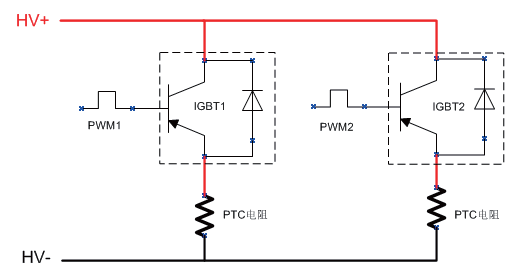
脈寬調制(PWM)開關本身就能很好地模擬一個反激式轉換器。由Dr. Vatché Vorpérian于90年代提出，最簡單的模擬一個工作于CCM模式的雙開關電壓模式DC-DC轉換器的大信號響應和固定開關頻率如圖3 。該原理包括平均兩個連接端之間的波形，“a”(有源)、“p”(無源)和“c”(共有的)以描述 一組連續時間的電流/電壓等式。Vorpérian表明，配置如圖3的電流和電壓源相當于考慮將理想的直流變壓器連接到終端 a-c-p，受匝數比d、占空比影響。

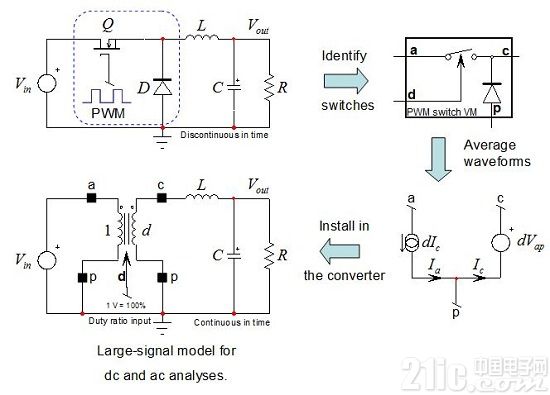
圖3：不可能有比PWM開關模型更簡單的了!

模型是不變的，說明它可替代其它DC-DC轉換器，所有描述這PWM開關的等式保持不變。圖3所示的模型是大信號版本。如果SPICE可提供這模型的小信號響應–因為SPICE是線性求解器，它將在運行仿真前將模型線性化–我們不能使用它的原型來確立控制-輸出傳遞函數。我們需要PWM開關的線性化或小信號版本。如圖4所示，您可看到通用架構，并看它如何轉化為工作中的SPICE模型。對那些對PWM開關的進一步詳細信息感興趣的，有詳盡介紹及大量工作實例。

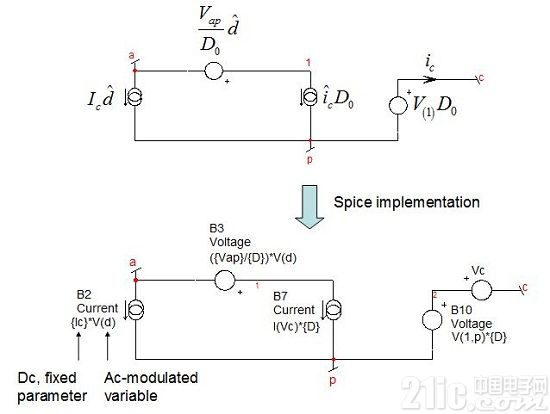
圖4：PWM開關的小信號版本使原型稍微復雜

請注意源包括幾個與產品的直流和交流值相關的術語。例如，系列源B3表示為{Vap}除以{D}，乘以V(d)。{Vap}代表端子“a”和“p”之間的穩態電壓，而{D}是穩態占空比。這些都是固定參數，對應于一個工作點。例如，圖3中降壓轉換器的{Vap}是Vin. d，占空比可以是在0和1 V(0至100%)之間的任意值。

圖5顯示了如何使用PWM開關模型仿真反激式轉換器，它與特定變壓器的等效比為1:d。框架電壓是由仿真器計算出的偏置點。驗證它們在適當的限度內很重要。有時結算器未能確定正確的操作點而是提供一個動態響應。這顯然是個錯誤的結果，必須丟棄它，直到找到一個新的正確的操作點。從第一部分，我們知道CCM反激式轉換器理想的(無漏電感)直流傳遞函數是

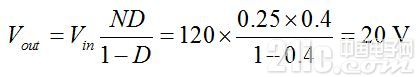
(1)

這是原理圖顯示的整個負載電阻：我們的偏置點是正確的。現在我們有了大信號模型，我們可在圖4 的基礎上推出小信號應用。為此，我們需要計算幾個固定參數，Vap和端子“c”的平均電流Ic。一旦您將PWM開關模型調整到適合反激式轉換器結構，在端子“a”和“p”之間的電壓Vap變為輸入電壓Vin減去反射電壓Vout/N(忽略次級二極管Vf)。由于這電壓是負數，我們有端子“c”的電流是流過初級電感Lp的平均電流。導通或dTsw期間這電流的一部分在端子“a”循環，關斷或 (1–d)Tsw期間流過端子“p”。圖7顯示端子“a”和“c”的典型的瞬時波形。根據圖5中的應用原理圖，端子“a”的平均電流也在輸入源循環以產生Pin:

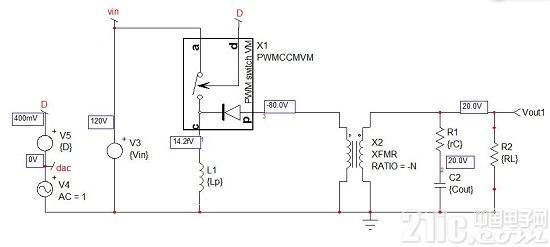
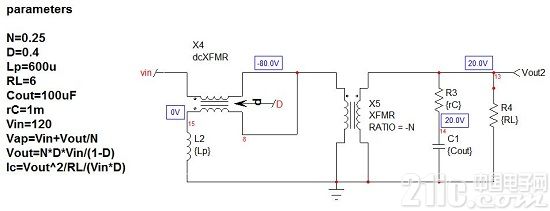
圖5：PWM開關模型用于CCM反激式轉換器的一個實際應用

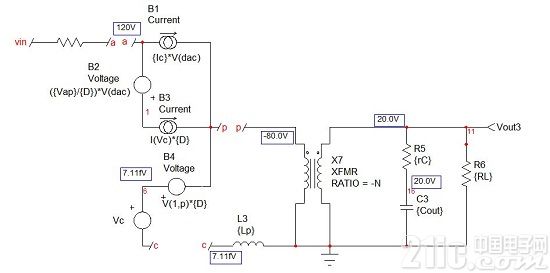
圖6：PWM開關模型的小信號版本僅需幾個控制源。

由圖7，我們可寫

(4)

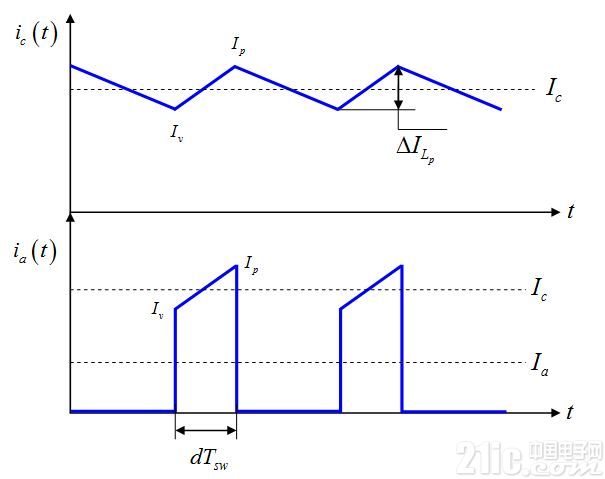
圖7：端子“c”的電流是初級電感Lp電流。