測量數據舍入算法

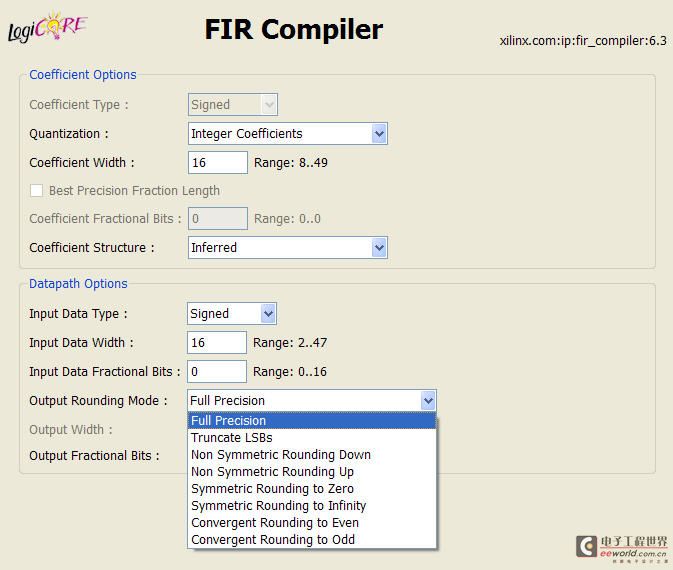
圖1

關于舍入算法有多種，主要有Round Toward Nearest、Round Ceiling、Round Floor和Truncation：

Round Toward Nearest

Rounding Toward Nearest就是通常所說的“四舍五入”，以5為有符號數為例，高3位為整數位（包含最高位符號位），低2位為小數位。如圖2所示，對5為有符號二進制數進行了舍入處理，舍去小數位，其中小數位大于0.5，整數位進1，小于0.5時不進位，而等于0.5時，舍入后數據打了問號，因為對于0.5的舍入處理，又可分為4種處理算法：

(1). Round Half Up；(2). Round Half Down；(3). Round Half Even；(4). Round Half Odd

并且以上第(1)、(2)種算法對應分別有對稱（Symmetric）和非對稱（Asymmetric）2類。

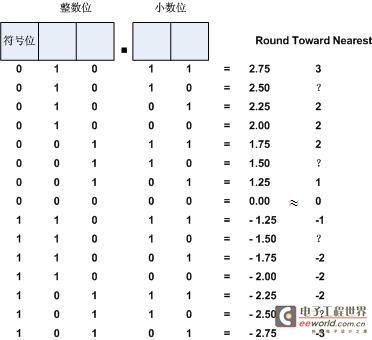
圖2

(1). Round Half Up

Round Half Up算法對于0.5的舍入處理為向上取值，因此此例中整數位進1，而這僅對正數部分而言，對于負數部分可按照相對于0對稱與否分為2類，如圖3所示。

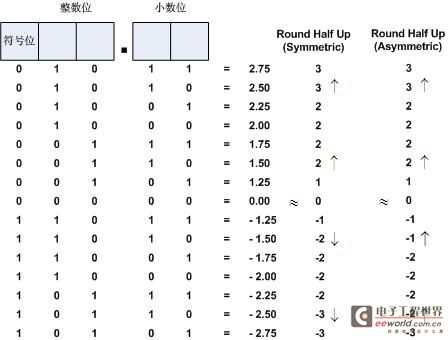
圖3

(2). Round Half Down

Round Half Down算法對于0.5的舍入處理為向下取值，因此此例中整數位不進，而這僅對正數部分而言，對于負數部分可按照相對于0對稱與否分為2類，如圖4所示。

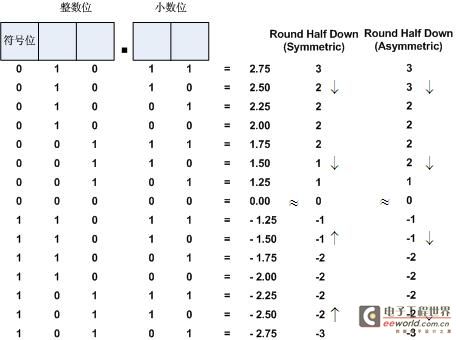
圖4

(3). Round Half Even

Round Half Even算法根據有效位來判斷是否進位，在此例中，舍去小數位，因此判斷整數位即可，如果整數位為偶數，則不進位，奇數則進位，因此舍入處理后整數位肯定是個偶數。如圖5所示，可以發現Round Half Even必然是Symmetric算法。