時(shí)鐘抖動(dòng)的定義與測(cè)量方式
1簡(jiǎn)介
本文引用地址:http://www.104case.com/article/201612/334042.htm抖動(dòng)是實(shí)際信號(hào)的一組邊沿與理想信號(hào)之間的偏差(兔子:說(shuō)白了,抖動(dòng)就是實(shí)際情況和理想情況不一樣,差別越大抖動(dòng)越大)。時(shí)鐘信號(hào)的抖動(dòng)通常由系統(tǒng)中的噪聲或其他干擾因素引起。影響因素包括熱噪聲、電源變化(波動(dòng))、負(fù)載的狀況(負(fù)載也可以反過(guò)來(lái)影響時(shí)鐘信號(hào))、設(shè)備噪聲和臨近電路耦合進(jìn)來(lái)的干擾。
2抖動(dòng)的分類
抖動(dòng)可以通過(guò)許多方式測(cè)量(不同方式測(cè)量到的抖動(dòng)被分別加以定義),以下是主要的抖動(dòng)分類:
1. 周期抖動(dòng)(Period Jitter)
2. 相鄰周期間的抖動(dòng)(Cycle to Cycle Period Jitter)
3. 長(zhǎng)時(shí)間抖動(dòng)(Long Term Jitter)
4. 相位抖動(dòng)(Phase Jitter)
5. 單位時(shí)間間隔抖動(dòng)(TIE,Time Interval Error)
2.1周期抖動(dòng)
周期抖動(dòng)是時(shí)鐘信號(hào)的實(shí)際周期長(zhǎng)度與理想周期長(zhǎng)度之間的偏差,測(cè)量樣本為數(shù)目不定(隨機(jī))的一組周期。如果給定一定數(shù)目的單個(gè)時(shí)鐘周期,我們就可以通過(guò)測(cè)量每個(gè)周期的長(zhǎng)度并計(jì)算平均的周期長(zhǎng)度,以及這些時(shí)鐘周期的標(biāo)準(zhǔn)差和峰峰值(peak-to-peak value)。這里所說(shuō)的標(biāo)準(zhǔn)差和峰峰值也分別被稱為RMS抖動(dòng)和Pk-Pk周期抖動(dòng)。
許多文獻(xiàn)將周期抖動(dòng)直接定義為被測(cè)時(shí)鐘周期與理想周期之間的誤差。但是真實(shí)情況下很難對(duì)理想周期進(jìn)行量化。如果我們用示波器觀察一個(gè)標(biāo)稱100MHz的晶振,測(cè)得的平均時(shí)鐘周期卻可能是9.998ns,而不是理想的10ns。所以退而求其次,通常將平均周期作為理想周期看待(兔子:因?yàn)閷?shí)際周期都是在理想值周圍按照一定規(guī)律分布的,如果測(cè)量時(shí)間足夠長(zhǎng),得到的平均值就可以非常接近理想值)。
2.1.1周期抖動(dòng)的應(yīng)用
周期抖動(dòng)對(duì)于計(jì)算數(shù)字系統(tǒng)的時(shí)序裕量十分有用。假設(shè)在一個(gè)基于微處理器的系統(tǒng)中(上升沿采樣),處理器要求1ns的數(shù)據(jù)建立時(shí)間(即數(shù)據(jù)需要在時(shí)鐘上升沿1ns前保持穩(wěn)定有效)。當(dāng)時(shí)鐘的某個(gè)周期抖動(dòng)為-1.5ns時(shí),上升沿會(huì)出現(xiàn)在數(shù)據(jù)有效之前,如此處理器將會(huì)采集到錯(cuò)誤的數(shù)據(jù)。如圖1所示:
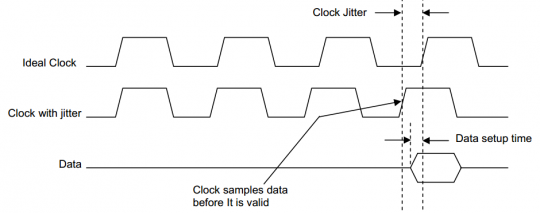
圖1時(shí)鐘抖動(dòng)造成的數(shù)據(jù)建立錯(cuò)誤
類似的,如果另一個(gè)處理器需要2ns的數(shù)據(jù)保持時(shí)間,但是時(shí)鐘某一個(gè)周期的抖動(dòng)是+1.5ns,那么實(shí)際有效的數(shù)據(jù)保持時(shí)間只有0.5ns,處理器也會(huì)采到錯(cuò)誤的數(shù)據(jù)。如圖2:
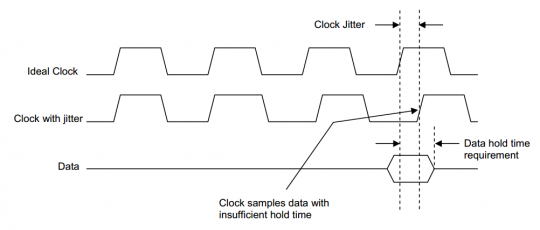
圖2時(shí)鐘抖動(dòng)造成的數(shù)據(jù)保持錯(cuò)誤
2.1.2由RMS抖動(dòng)計(jì)算Pk-Pk抖動(dòng)
由于時(shí)鐘的周期抖動(dòng)是隨機(jī)的,并遵循高斯分布。因此周期抖動(dòng)完全可以用統(tǒng)計(jì)學(xué)中的均方根(RMS ,Root Mean Square,別說(shuō)不會(huì)算)來(lái)表示,單位為皮秒(ps)。但是呢,峰峰值卻和計(jì)算建立保持時(shí)間裕量有更大的聯(lián)系(峰峰值表示了最大誤差,超過(guò)建立保持時(shí)間要求,數(shù)據(jù)采樣就有可能出錯(cuò))。要將10000個(gè)時(shí)鐘周期的RMS抖動(dòng)換算成Pk-Pk抖動(dòng),可遵循以下等式:
Pk-Pk周期抖動(dòng)=7.44 x RMS抖動(dòng) *等式1
例如:若RMS抖動(dòng)為3ps,則Pk-Pk周期抖動(dòng)為7.44 x 3 = ±11.16ps。
等式1其實(shí)是由高斯概率密度函數(shù)表(PDF ,Gaussian Probability Density Function)推導(dǎo)出來(lái)的。比如當(dāng)樣本個(gè)數(shù)為100時(shí),從統(tǒng)計(jì)學(xué)的平均情況來(lái)講,其中 99個(gè)會(huì)落在有效值周圍的±2.327σ范圍內(nèi),只有1個(gè)會(huì)落在該范圍之外。根據(jù)JEDEC標(biāo)準(zhǔn)的要求,某司測(cè)量RMS周期抖動(dòng)時(shí)設(shè)定的樣本數(shù)為10000。
樣本數(shù) | σ |
10 | ±1.282 |
100 | ±2.327 |
1,000 | ±3.090 |
10,000 | ±3.719 |
100,000 | ±4.265 |
1,000,000 | ±4.754 |
10,000,000 | ±5.200 |
100,000,000 | ±5.612 |
1,000,000,000 | ±5.998 |
10,000,000,000 | ±6.362 |
100,000,000,000 | ±6.706 |
1,000,000,000,000 | ±7.035 |
表1高斯概率密度函數(shù)表(PDF)
2.1.3周期抖動(dòng)測(cè)量方式
JEDEC Standard 65B中將周期抖動(dòng)定義為某一隨機(jī)數(shù)量的時(shí)鐘周期與理想周期之間的偏差(由定義了一次,生怕大家忘了)。JEDEC標(biāo)準(zhǔn)進(jìn)一步地指定了測(cè)周期抖動(dòng)需要測(cè)量10000個(gè)信號(hào)周期(多一個(gè)少一個(gè)應(yīng)該也無(wú)所謂吧)。某司推薦的測(cè)試步驟如下:
1. 測(cè)量一個(gè)時(shí)鐘周期(一個(gè)上升沿到下一個(gè)上升沿之間)的長(zhǎng)度,即一個(gè)樣本
2. 等待隨機(jī)個(gè)時(shí)鐘周期
3. 重復(fù)1、2兩步10000次
4. 通過(guò)測(cè)到的10000個(gè)樣本,計(jì)算平均值,標(biāo)準(zhǔn)差(σ),和峰峰值
5. 重復(fù)1-4步驟25次,通過(guò)這25組結(jié)果,計(jì)算平均峰峰值
10000個(gè)隨機(jī)樣本計(jì)算出的標(biāo)準(zhǔn)差(σ),即均方根(RMS,也有人認(rèn)為均方根和標(biāo)準(zhǔn)差并非等同)已經(jīng)很精確了,RMS的誤差可以通過(guò)如下等式計(jì)算:
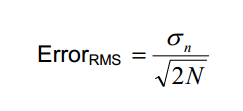 *等式2
*等式2
等式中的σn為樣本的RMS,N為樣本數(shù)。
例如:樣本數(shù)為10000,RMS誤差為0.0071 σn。這種誤差是隨機(jī)的,并且遵從高斯分布,通常用±3 x RMS誤差來(lái)計(jì)算最大測(cè)量誤差。
又例如:如果從10000個(gè)樣本中計(jì)算出RMS為10ps,則RMS誤差為0.071ps,所有RMS值都會(huì)落在10 ± 0.213ps(RMS ± 3 x RMS誤差)的范圍內(nèi)。在實(shí)際應(yīng)用中,若只有10000樣本,RMS誤差可以忽略不計(jì)。
Q: 為什么要用均方根來(lái)計(jì)算峰峰值?
A:一定數(shù)量的隨機(jī)樣本就能夠精確計(jì)算出均方根,但是想要測(cè)量實(shí)際的峰峰值卻非常困難。由于周期抖動(dòng)的隨機(jī)性,樣本數(shù)量越大則越有可能測(cè)量到落在高斯分布曲線遠(yuǎn)端的樣本,換言之峰峰值隨采樣數(shù)量增加發(fā)散,而非收斂。
Q:為什么需要步驟5(重復(fù)25次)?
A:每測(cè)量10000個(gè)樣本,就可以算出一個(gè)標(biāo)準(zhǔn)差(均方根)和峰峰值。而隨機(jī)地重復(fù)該步驟25次,我們就可以計(jì)算很高精度的的平均峰峰值。這增加了峰峰值測(cè)量的一致性和可重復(fù)性。(兔子:就是說(shuō)每次直接測(cè)250000個(gè)數(shù)據(jù)計(jì)算出的峰峰值一致性不好,這樣分開(kāi)測(cè)就好啦?有待驗(yàn)證……)
圖3為某125MHz晶振的周期抖動(dòng)直方圖,同時(shí)顯示了10000個(gè)樣本中測(cè)得的RMS和Pk-Pk抖動(dòng)。
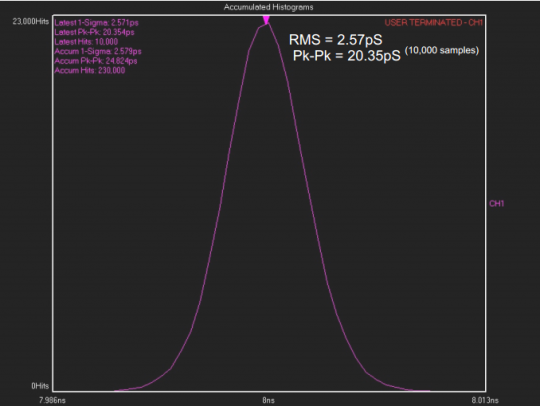
圖3 10000個(gè)樣本的周期抖動(dòng)直方圖
2.2相鄰周期抖動(dòng)
JEDEC 65B標(biāo)準(zhǔn)將相鄰周期抖動(dòng)(C2C,Cycle to cycle)定義為信號(hào)相鄰周期之間的時(shí)間長(zhǎng)度變化,前提也是測(cè)量不定數(shù)量(隨機(jī))的相鄰周期長(zhǎng)度差,綜合后得到的結(jié)果。JEDEC標(biāo)準(zhǔn)也進(jìn)一步指定了每個(gè)樣本集的樣本數(shù)應(yīng)該大于或等于1000(就是采集1000對(duì)相鄰周期)。需要注意的是C2C抖動(dòng)只關(guān)注兩個(gè)連續(xù)周期之間的周期長(zhǎng)度變化,并不參考任何理想時(shí)鐘。
C2C抖動(dòng)一般用峰值表示,有時(shí)候也用均方根表示,單位是ps。該參數(shù)定義了一個(gè)時(shí)鐘信號(hào)的任意兩個(gè)連續(xù)周期間長(zhǎng)度變化的最大值(以上升沿為標(biāo)準(zhǔn))。此類抖動(dòng)常被用于體現(xiàn)帶有擴(kuò)頻(SSC,spread spectrum clock)特性時(shí)鐘的穩(wěn)定性,原因是周期抖動(dòng)對(duì)擴(kuò)頻(頻率值會(huì)發(fā)生變化)很敏感,C2C抖動(dòng)則不然。
2.2.1相鄰周期抖動(dòng)測(cè)量方式
1. 測(cè)量某時(shí)鐘的兩個(gè)相鄰周期的長(zhǎng)度:T1和T2
2. 計(jì)算T1-T2,取絕對(duì)值
3. 等待隨機(jī)個(gè)時(shí)鐘周期
4. 重復(fù)1-3步驟1000次
5. 計(jì)算標(biāo)這1000個(gè)樣本的準(zhǔn)差(σ)和峰值,峰值為|T1-T2|的最大值
6. 重復(fù)1-5步驟25次,計(jì)算25個(gè)峰值的平均值
與周期抖動(dòng)的峰峰值類似,C2C抖動(dòng)的峰值也是隨樣本數(shù)發(fā)散的。第6步用于獲取平均峰值(以增加測(cè)試結(jié)果的一致性和可重復(fù)性)。
圖4為某時(shí)鐘C2C抖動(dòng)的直方圖,這里抖動(dòng)峰值為25.66ps(正負(fù)峰值21.22ps和-25.66ps中取最大值)。
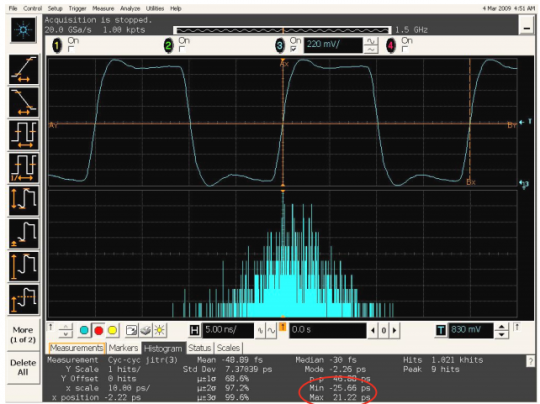
圖4 C2C抖動(dòng)直方圖
2.3長(zhǎng)期抖動(dòng)
長(zhǎng)期都懂用于測(cè)量一組連續(xù)時(shí)鐘周期中實(shí)際時(shí)鐘與理想四種的差異。實(shí)際需要測(cè)量多少個(gè)周期由應(yīng)用場(chǎng)合決定。長(zhǎng)期抖動(dòng)與周期抖動(dòng)、相鄰周期抖動(dòng)不同,它表示一段長(zhǎng)時(shí)間、連續(xù)的時(shí)鐘信號(hào)流中存在的抖動(dòng)累積效應(yīng),因此長(zhǎng)期抖動(dòng)也被稱為累計(jì)抖動(dòng)。長(zhǎng)期抖動(dòng)的典型應(yīng)用為圖片及視頻顯示、遠(yuǎn)程遙感勘測(cè)及測(cè)距儀。
某司推薦的測(cè)量長(zhǎng)期抖動(dòng)方法如下(以10000個(gè)時(shí)鐘周期為例):
1. 測(cè)量10000個(gè)周期的總時(shí)間長(zhǎng)度,如圖5所示
2. 等待隨機(jī)個(gè)時(shí)鐘周期
3. 重復(fù)1-2步驟1000次
4. 計(jì)算這1000個(gè)樣本的有效值、標(biāo)準(zhǔn)差和峰峰值
5重復(fù)1-4步驟25次,取25次峰峰值的平均值
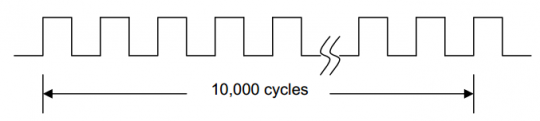
圖5測(cè)量10000個(gè)時(shí)鐘周期的總時(shí)長(zhǎng)
同理,我們需要通過(guò)步驟5來(lái)克服峰峰值的無(wú)邊界分布特性。
2.4相位抖動(dòng)
相位噪聲通常被描述為在不同頻率下的一組噪聲值(如-60 dBc/Hz @ 20KHz 和 -95 dBc/Hz @ 10MHz),或者表示為一段連續(xù)頻率范圍內(nèi)的噪聲圖。相位抖動(dòng)則是一段特定頻譜中相位噪聲綜合的結(jié)果,其單位是秒。
對(duì)于方波而言,其主要能量集中在載波頻率上,但一些能量仍會(huì)在載波頻率兩側(cè)的一定頻率范圍內(nèi)“泄露”(leaked-out)出去。相位抖動(dòng)就是與載波頻率fc相關(guān)的兩個(gè)指定頻率之間的相位噪聲能量總和。圖6是一個(gè)未經(jīng)濾波的相噪圖,陰影區(qū)域即表示f1至f2頻率之間的相位抖動(dòng)。
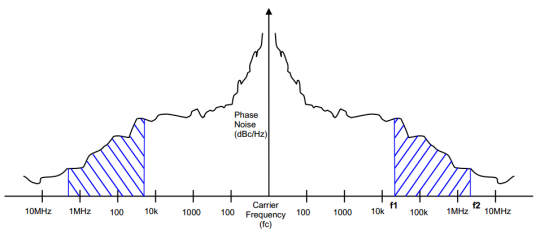
圖6相噪圖
頻率f1與f2之間的RMS相位抖動(dòng)可以用等式3表示:
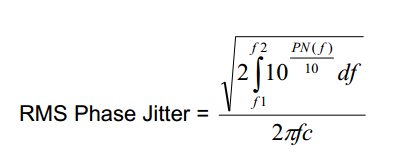 *等式3
*等式3
其中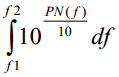 表示fc一側(cè)f1-f2之間的噪聲功率。在通信領(lǐng)域中,通信接口的發(fā)送端 PLL和接收端 PLL存在帶通濾波效,因此在實(shí)際情況下我們需要根據(jù)濾波器的特性計(jì)算濾波后的RMS相位抖動(dòng)。以下為常見(jiàn)通信接口對(duì)應(yīng)帶通濾波器的帶寬(拐點(diǎn)頻率),這些帶寬是綜合了發(fā)送和接收端PLL特性得到的結(jié)果:
表示fc一側(cè)f1-f2之間的噪聲功率。在通信領(lǐng)域中,通信接口的發(fā)送端 PLL和接收端 PLL存在帶通濾波效,因此在實(shí)際情況下我們需要根據(jù)濾波器的特性計(jì)算濾波后的RMS相位抖動(dòng)。以下為常見(jiàn)通信接口對(duì)應(yīng)帶通濾波器的帶寬(拐點(diǎn)頻率),這些帶寬是綜合了發(fā)送和接收端PLL特性得到的結(jié)果:
1. 光纖接口: 637 KHz ~ 10 MHz
2. 10GE XAUI接口:1.875 MHz ~ 20 MHz
3. SATA/SAS接口: 900 KHz ~ 7.5 MHz
假設(shè)濾波器函數(shù)為H(f),則濾波后的RMS相位抖動(dòng)可以用等式4計(jì)算:
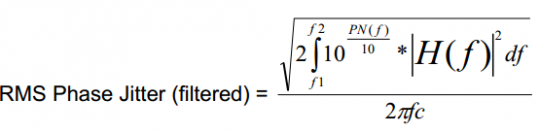 *等式4
*等式4
3單位時(shí)間間隔誤差
單位時(shí)間間隔誤差(TIE,Time Interval Error)是指在擁有參考點(diǎn)(兔子:用于參考的時(shí)鐘邊沿,在該點(diǎn)實(shí)際時(shí)鐘與理想時(shí)鐘邊沿對(duì)齊)的情況下,信號(hào)的某個(gè)實(shí)際邊沿與理想邊沿間的時(shí)間差。事實(shí)上,TIE是相位噪聲在離散時(shí)間域上的表現(xiàn),單位為秒或皮秒。圖7形象地描述了TIE的基本概念。理想信號(hào)通常是由軟件對(duì)被測(cè)信號(hào)的周期進(jìn)行平均估計(jì)得到的。
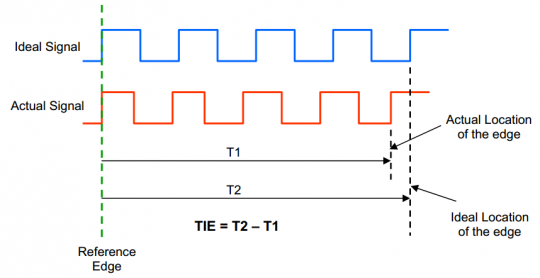
圖7測(cè)量單個(gè)信號(hào)邊沿的TIE
3.1繪制時(shí)域TIE圖
圖8的最上面一行是一組時(shí)鐘的的波形,紅色表示周期為1000ps的理想時(shí)鐘,黑色表示帶有抖動(dòng)的實(shí)際時(shí)鐘。為了方便表示,只畫出了時(shí)鐘的上升沿。在時(shí)鐘序列的開(kāi)始,理想邊沿與實(shí)際邊沿重合(以此作為參考點(diǎn)),之后由于抖動(dòng),黑色的實(shí)際時(shí)鐘邊沿開(kāi)始隨著時(shí)間漂移,時(shí)而領(lǐng)先時(shí)而落后于紅色的理想時(shí)鐘。
圖中的Clock Period曲線表示所測(cè)得黑色時(shí)鐘的各個(gè)周期長(zhǎng)度。本例中黑色時(shí)鐘不是990ps就是1010ps(為了方便理解,理想化了,和第一行也不太對(duì)的上,湊合看吧)。
Period Change曲線則描述了每個(gè)時(shí)鐘周期與前一個(gè)周期的變化量。如果黑色時(shí)鐘的兩個(gè)相鄰周期長(zhǎng)度相同,那么Period Change曲線就會(huì)保持平坦,反之就會(huì)發(fā)生變化。例如:……(兔子就不舉例了都能看懂)總而言之該曲線描繪了時(shí)鐘周期的變化。
TIE曲線則記錄了理想邊沿和實(shí)際邊沿之間的累計(jì)誤差。此一例中,TIE曲線開(kāi)始時(shí)向下增長(zhǎng),這是由于最初的四個(gè)時(shí)鐘周期里每個(gè)實(shí)際周期都比理想周期長(zhǎng)度要少10ps。在累積了-40ps的抖動(dòng)誤差后,曲線從第5個(gè)周期開(kāi)始向上增長(zhǎng),這也是由于第5個(gè)時(shí)鐘的實(shí)際周期比理想周期多10ps。
TIE測(cè)量在檢驗(yàn)數(shù)據(jù)流(通常是串行通信接口)的特性時(shí)非常有用,這些傳輸接口的時(shí)鐘通常由時(shí)鐘數(shù)據(jù)恢復(fù)(CDR,Clock/Data Recovery )電路從數(shù)據(jù)信號(hào)中恢復(fù)出來(lái)。比如較大的TIE值可能就說(shuō)明了CDR中PLL的響應(yīng)速度太慢了跟不上數(shù)據(jù)流的數(shù)據(jù)變化速率。
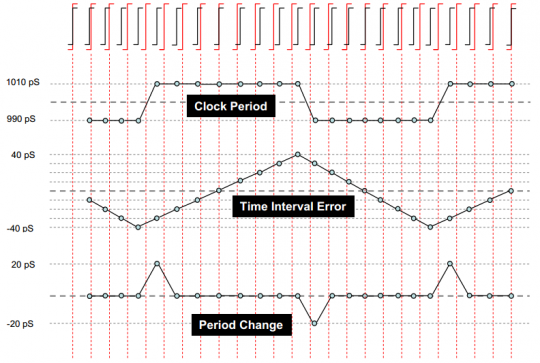
圖8 TIE圖
4采用實(shí)時(shí)示波器測(cè)量抖動(dòng)
4.1示波器設(shè)置指導(dǎo)
測(cè)量時(shí)鐘抖動(dòng)最通用的設(shè)備當(dāng)屬實(shí)時(shí)數(shù)字示波器,本章將為大家介紹如果設(shè)置示波器以達(dá)到更高的測(cè)量精度。
數(shù)字示波器采用內(nèi)部時(shí)間基準(zhǔn)來(lái)定期采樣輸入的數(shù)據(jù),其采樣率可由1Gsps到40Gsps不等。圖9列舉了數(shù)字示波器采樣和顯示信號(hào)的方式。圖底部的箭頭表示采樣點(diǎn),實(shí)線是實(shí)際的信號(hào),黑點(diǎn)為采樣得到的數(shù)據(jù),而示波器顯示出的圖像(虛線)為根據(jù)采樣數(shù)據(jù)經(jīng)過(guò)優(yōu)化得到的曲線。
也許你會(huì)發(fā)現(xiàn)采樣值與實(shí)際信號(hào)并不一致,這是因?yàn)槭静ㄆ髁炕倪^(guò)程中存在誤差。大多數(shù)誤差是因?yàn)槭静ㄆ鳛榱嗽谠O(shè)計(jì)性能和成本之間尋求平衡而帶來(lái)的固有誤差,但我們通過(guò)適當(dāng)?shù)脑O(shè)置可以緩解為了省錢帶來(lái)的精確度問(wèn)題。下面我們就就來(lái)探討一下造成這些誤差的主要原因以及如果通過(guò)設(shè)置來(lái)降低他們對(duì)抖動(dòng)測(cè)量的影響。
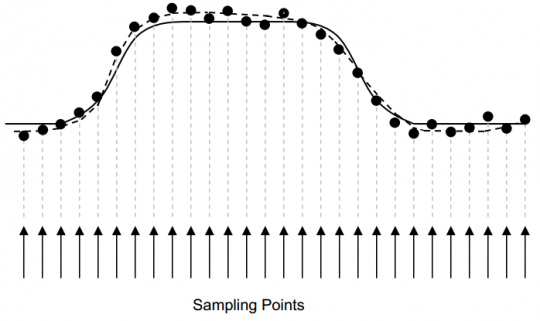
圖9數(shù)字示波器的采樣及顯示
4.1.1前端放大器誤差
數(shù)字示波器的輸入信號(hào)要經(jīng)過(guò)模擬放大器才能被ADC數(shù)字化,而放大器產(chǎn)生的噪聲與示波器輸入帶寬成正比:帶寬越寬,噪聲越大(兔子:這也是測(cè)電源紋波的時(shí)候要限制帶寬的原因)。但是一位地減小帶寬會(huì)影響示波器對(duì)信號(hào)上升和下降時(shí)間的采樣,也會(huì)引入很大的誤差。
這里有一個(gè)通用的描述信號(hào)邊沿上升/下降時(shí)間和貸款關(guān)系的等式:
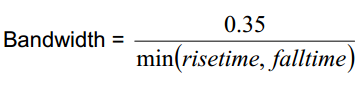 *等式5
*等式5
其中上升時(shí)間或下降時(shí)間測(cè)量位置為信號(hào)邊沿電平的20%~80%之間。某司推薦將示波器帶寬設(shè)置為信號(hào)帶寬的3倍(另有某司出面認(rèn)為3倍不足以還原信號(hào)邊沿的細(xì)節(jié),至少應(yīng)為5倍),另外在一些示波器中,帶寬只能隨著最高采樣率的設(shè)置改變,甚至有的示波器帶寬完全不能設(shè)置。
4.1.2垂直增益引起的量化噪聲
量化誤差是指采樣值與采樣點(diǎn)實(shí)際信號(hào)值之間的差別,這種誤差如圖9所示。引起這種誤差的一部分因素來(lái)自于為調(diào)整示波器Y軸顯示而設(shè)置的垂直增益。如果垂直增益過(guò)小,示波器可能無(wú)法有效利用內(nèi)部ADC的完整分辨率(很多示波器只有8位的AD)。
某司推薦調(diào)整示波器垂直增益直至波形撐滿屏幕Y軸。某些示波器中甚至可以將波形調(diào)至略微超出Y軸顯示范圍,從而使用ADC的額外bit位。不過(guò)這一特性取決于你使用的示波器,具體可以咨詢廠家。
4.1.3低采樣率引起的量化噪聲
還有一部分量化噪聲是由于示波器橫軸方向采樣點(diǎn)數(shù)不足造成的。某司推薦在信號(hào)上升/下降沿的20%~80%電平間至少有3個(gè)采樣點(diǎn),由此可以推出示波器設(shè)置的最低采樣率要求。例如,如果信號(hào)上升時(shí)間1ns并且需要在這段時(shí)間里保證4個(gè)采樣點(diǎn),那么示波器至少要設(shè)置4Gsps的采樣率。如果你的示波器性能高于這個(gè)標(biāo)準(zhǔn),那么就越大越好啦,設(shè)置成最高采樣率(實(shí)際上除了限制帶寬以外,大部分的示波器軟件都能根據(jù)實(shí)際信號(hào)自動(dòng)調(diào)節(jié)到最佳的橫軸和縱軸)。
4.1.4時(shí)間基準(zhǔn)抖動(dòng)
數(shù)字示波器采樣點(diǎn)的選擇源于內(nèi)部時(shí)間基準(zhǔn)。作為一個(gè)時(shí)鐘源,時(shí)間基準(zhǔn)自身存在抖動(dòng),并且會(huì)增加測(cè)量信號(hào)抖動(dòng)時(shí)的誤差。一般來(lái)說(shuō),時(shí)基抖動(dòng)應(yīng)該小于被測(cè)信號(hào)抖動(dòng)期望值的25%,從而達(dá)到優(yōu)于3%的準(zhǔn)確度。某司推薦使用你實(shí)驗(yàn)室里最好的示波器來(lái)進(jìn)行抖動(dòng)測(cè)量,因?yàn)楦叨说脑O(shè)備往往擁有更好(更低抖動(dòng))的時(shí)基電路(好一通廢話啊哈哈)。
4.2使用實(shí)時(shí)示波器測(cè)量抖動(dòng)的步驟
(本節(jié)內(nèi)容基本與2.1-2.3節(jié)所述雷同,故不做翻譯)
4.2.1測(cè)量周期抖動(dòng)
4.2.2測(cè)量相鄰周期抖動(dòng)
4.2.3測(cè)量長(zhǎng)期抖動(dòng)
5結(jié)論
本文著成之初有兩個(gè)目的:其一,向讀者描述今日之高速系統(tǒng)中所能遇見(jiàn)的一般抖動(dòng)類型;其二,提供借由實(shí)時(shí)示波器來(lái)捕獲不同種類抖動(dòng)的方法步驟。兔子翻譯此文之目的 已于文前盡言,不復(fù)贅述。



評(píng)論