淺談數字化寬帶測向系統中的相位差測量及誤差

　　在電子對抗領域中輻射源測向是一個基本問題。能發射電離輻射的物質或裝置。從廣義上講，凡能釋放各種電離輻射的物質或裝置（如宇宙射線）均可視為輻射源。但習慣上用于γ探傷、放射治療和輻射加工等的放射性深度較高的放射源稱為輻射源。干涉儀測向體制的主要優點是精度高和工作頻率范圍寬，但目前使用的干涉儀系統還存在不足，主要包括：（1）在被動制導等領域中測向精度仍然不夠：（2）對現代雷達使用的寬帶脈壓信號適應能力有限；（3）有待進一步提高系統的工作頻率范圍。針對上述問題，本系列論文提出了數字化寬帶測向系統的整體解決方案，重點討論數字化相位差測量及誤差分析、概率解模糊算法和在測向精度和工作頻率范圍約束下如何進行天線陣列基線設計三個問題。

　　本文是系列論文的第一篇，給出了數字化寬帶測向系統模型，討論了數字化相位差測量方法，推導了數字化相位測量的數字化方法誤差函數和由通道噪聲引起的信號相位誤差分布密度函數。相位差測量的精度直接影響系統測向的精度，還會影響解相位差模糊和天線陣列基線設置等一系列系統設計問題。傳統的相位差測量方法都是利用窄帶信號干涉原理把相位差轉化為幅度進行測量的，因而其只能夠適用于窄帶信號的相位差測量，且測量精度受幅度測量誤差的影響較大。本文提出的數字化相位差測量方法，其基本思想是把信號轉換到頻率域，利用信號的相位譜直接完成在給定頻率點上相位差的測量，且全面的分析了相位差測量誤差。

　　1 數字化寬帶測向系統模型

　　數字化就是將許多復雜多變的信息轉變為可以度量的數字、數據，再以這些數字、數據建立起適當的數字化模型，把它們轉變為一系列二進制代碼，引入計算機內部，進行統一處理，這就是數字化的基本過程。解釋二：數字化將任何連續變化的輸入如圖畫的線條或聲音信號轉化為一串分離的單元，在計算機中用0和1表示。通常用模數轉換器執行這個轉換。當今時代是信息化時代，而信息的數字化也越來越為研究人員所重視。早在40年代，香農證明了采樣定理，即在一定條件下，用離散的序列可以完全代表一個連續函數。就實質而言，采樣定理為數字化技術奠定了重要基礎。英文digit譯成“數字”是大陸的譯法。最開始是不是由原信產部的研究所科研人員這樣譯出，尚不可考，愿有心有力者相助查尋。

　　非均勻線陣的天線數為m，天線的間距分別為d1，d2，L dm-1寬帶入射信號分別為s（t），入射方向與陣列法線的交角分別為θ。

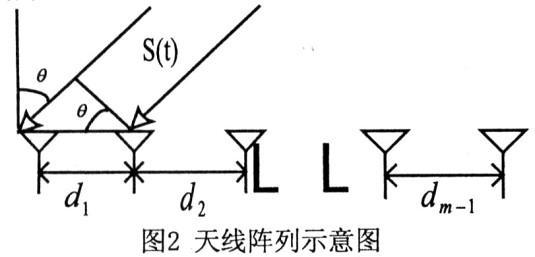
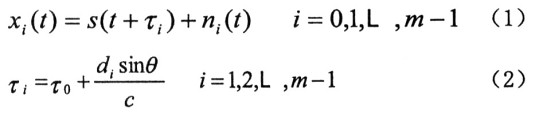
　　其中τ信號在第i個天線上相對于第O個天線的時間延遲，c是光速常數，di（l=1，2，L，m一1）為天線間距。對式（2）兩邊同做傅立葉變換：

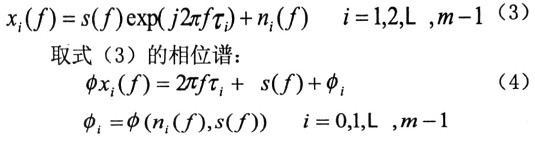
　　式（4）中φs（f）表示信號s的相位譜；φi為由噪聲譜對信號相位譜影響產生的誤差。作如下的相位差變換：

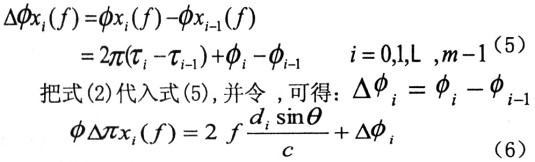
　　式（6）中相位差△φxi（f）是無模糊的相位差。然而實際中由于天線陣列的間距大于半波長因而相位差是有模糊的。

　　不妨令：

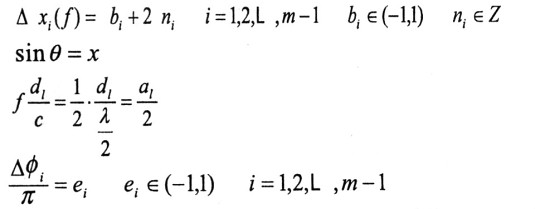
　　式中bi是有模糊的相位差，ni表示模糊整數，ai為相對基線長度，ei為相位差誤差。則式（6）可代換為：

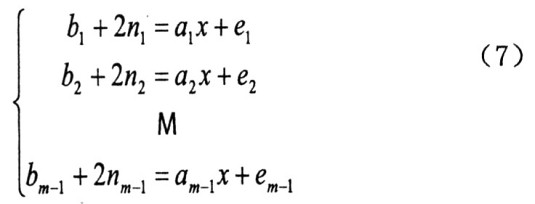
　　這是數字化寬帶測向系統模型。

　　以下的工作都是圍繞這個模型展開。其一是如何測量相位差bi（i=1，2，L，m一1） 及推導相位差測量誤差ei（i=l，2，L，m一1）的分布密度函數。其二是如何快速求解模糊整數ni（i=1，2，L，m一1），即快速解模糊問題，這將在第二篇論文中討論。其三是如何求解x的最優估計值從而獲得測向角θ=arcsin（x），并進行測向角測量誤差分析；同時還會討論如何進行天線陣列的設計問題。

　　2 數字化相位差測量及數字化方法誤差

　　不妨設兩個通道的時延為τ，信號為△t，信號持續時間為s（t），采樣間隔為N，采樣點數為T。

　　式（14）即為相位差測量的數字化方法誤差函數。

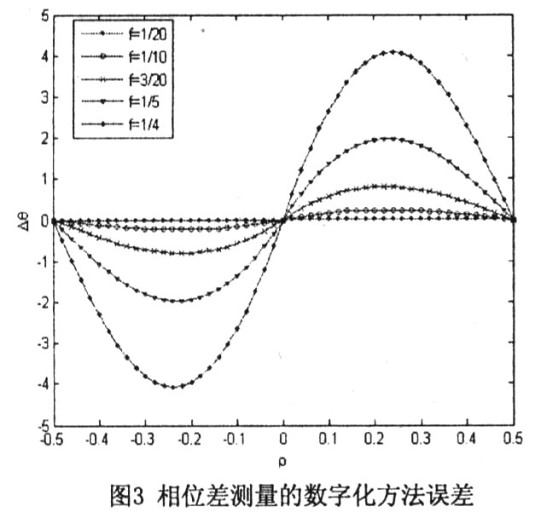
　　從圖3中可以看出：在f=1／4，即采樣頻率是所測頻率的4倍時，相位差最大誤差約為40；當采樣頻率是所測頻率的20倍時，方法誤差可以忽略。

　　3通道高斯白噪聲引起的信號相位誤差設通道噪聲是高斯白噪聲N（O，σ2），采樣點數為N。則有：（1）其在離散傅立葉變換序列的實部序列和虛部序列是獨立同分布的高斯白噪聲序列（證明略）。（2）噪聲的幅度譜服從瑞利分布，相位譜服從均勻分布（證明略）。（3）噪聲對信號相位譜的影響。

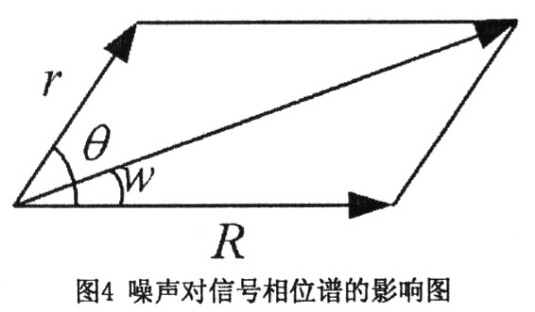
　　圖4中，R為信號頻譜幅度值，r，θ為噪聲頻譜幅度值和相角，w為噪聲引起的信號相位誤差。

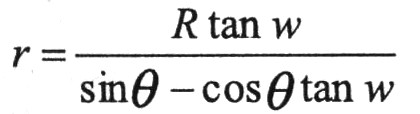
　　令θ’=θ，則有：

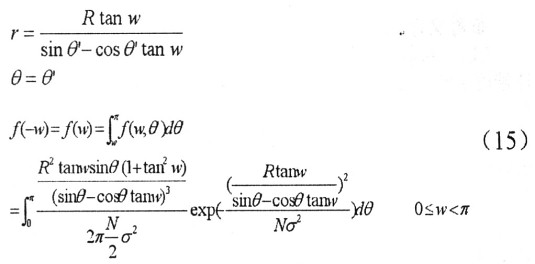
　　設噪聲的歸一化帶寬為B，信號的幅度一致性系數為ρ，白噪聲功率為σ2，信噪比為SN，則計算噪聲對信號的相位譜的影響關系。其中ρ義為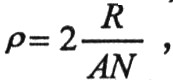通過簡單證明可得的零直流分量信號的幅度一致性系數ρ≤1。則：

　　式（16）即為噪聲引起的相位誤差分布密度函數。

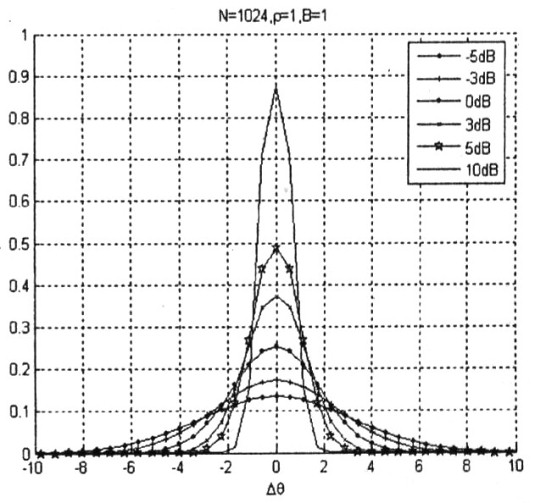
　　圖6噪聲引起的相位誤差分布密度函數和信噪比的關系

　　圖6中顯示，由通道高斯白噪聲引起的信號相位誤差分布近似于高斯分布。

　　4 結束語

　　本文主要給出了數字化寬帶測向系統模型（式（7））和數字化相位差測量的原理公式（式（13）），推導了相位差測量的數字化方法誤差函數（式（14））和由通道高斯白噪聲引起的信號相位誤差分布密度函數（式（16））。