基于神經網絡優化的油水界面軟測量
原油脫水過程中油水界面的準確監測對油品的含水率、污水回收及處理成本都是極為關鍵的,能開發出在線的測量技術具有十分重要的現實意義。
遺傳算法和神經網絡都是將生物學原理應用于科學研究的仿生學理論成果,由于它們具有極強的解決問題的能力,近年來引起了眾多科研人員和工程人員的興趣和關注[1]。但神經網絡和遺傳算法作為傳統的算法,不僅計算量大,消耗時間多,而且還需要專家進行校驗[2-4]。因此,為了充分利用兩種算法的優勢,彌補兩者之間的缺陷,本文采用了將兩者結合的思想。
2 問題描述
在基于BP算法的多層前饋網絡的應用中,以圖1所示的單隱層網絡的應用最為普遍。一般習慣將單隱層前饋網絡稱為三層前饋網或三層感知器,所謂的三層包括了輸入層、隱層和輸出層。隱層可以是單層,也可以是多層,前層至后層節點通過權連接。
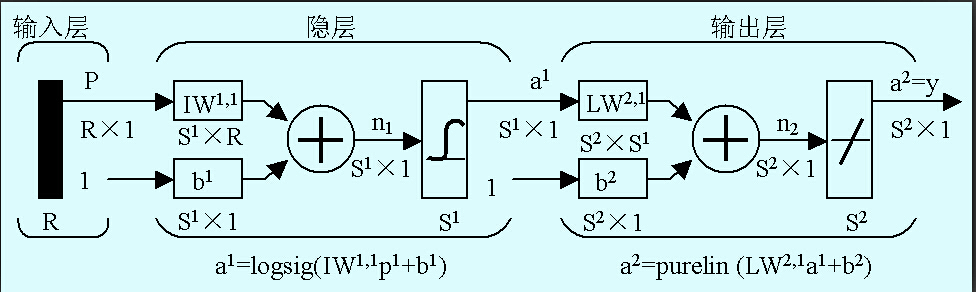
圖1 BP網絡結構
輸入矢量維數為R,隱層神經元的個數為S1,輸出層神經元的個數S2,a1表示隱層神經元的輸出矢量,a2表示輸出層神經元的輸出矢量,W1,1表示隱層神經元域為任一集合。對適應度函數唯一的要求是輸入可計算出能加以比較的非負結果。適應度函數具體的計算方法為:將染色體上表示的各個參數分配到BP網絡的結構上,結合訓練樣本集的輸入與輸出,計算網絡的輸出后得到網絡實際輸出與希望輸出的誤差,取誤差平方和作為目標函數,即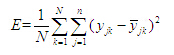 (3)
(3)
式中為網絡輸入輸出樣本對個數;為輸出層節點個數;,為當輸入第個樣本時,第個輸出節點的期望輸出與實際輸出。
遺傳算法以適應度函數作為進化目標,且只能朝著適應度函數值增大的方向進化,所以適應度函數與目標函數之間要進行適當的轉換。由于進化中的網絡誤差是非零正數,可將目標函數的倒數作為適應度函數,即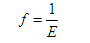 c) 遺傳算子的選擇。
c) 遺傳算子的選擇。
① 用輪盤賭法確定選擇算子,種群中個體的選擇概率為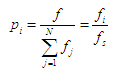 (5)
(5)
式中
為個體的適應度;
為種群的總適應度;
為個體的選擇概率。
輪盤賭法的具體實現是:先計算出當前種群的總適應度,然后產生一個[0,1]之間的隨機數,求取,并將滿足下列條件的第個個體選中,進入交叉操作: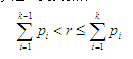 (6)
(6)
進行次這樣的操作,得到個個體,與最優選擇機制保留下來的適應度最大的個體,一起構成個個體,進入接下來的交叉和變異操作。
② 采用自適應的交叉概率的算法,使群體中最大適應度值的個體的交叉率和變異率不為零,分別得到提高,這就相應地提高了群體中表現優良的個體的交叉率和變異率,使得它們不會處于一種近似停滯不前的狀態。
種群中個體的交叉概率為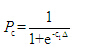 (7)
(7)
其中為常數;為“早熟度”,用來評價種群是否早熟的指標,其計算公式為,其中表示種群中個體適應度的最大值,表示個體適應度大于整體平均適應度的個體的平均適應度。
在二進制編碼中,采用的是單點或多點交叉。對于實數編碼來說,采用這些方法是困難的,本文采用算數交叉,即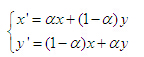 (8)
(8)
式中,為父代個體;,是子代個體;為(0,1)間的實數。
交叉時由于碼串選取的是最大可能長度,不會產生混亂現象。
③ 采用自適應的變異概率的算法,使遺傳算法具有局部的隨機搜索能力,在接近最優解的鄰域時加速向最優解收斂,維持種群多樣性,防止出現不成熟收斂。
種群中個體的交叉概率為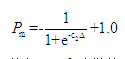 (9)
(9)
其中為常數。
非一致變異算子可以增強局部搜索能力,因此本文采用非一致變異操作進行算子的變異。假設為父代種群中的一個個體,其中。隨機選取中的一個基因,假設為第個基因,進行變異,則子代個體為。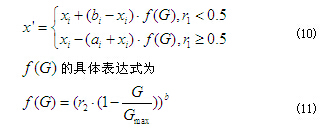



評論