一種基于移動基站的無線傳感器網絡數據收集方法

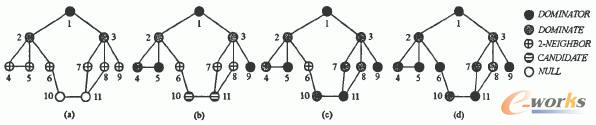
圖3 構建支配集的分布式算法簡單示例

2．3路徑優化

確定支配集后，基站還需要獲取各個節點的位置信息，選擇經過這些節點的一條較短的路徑。在支配集構建時，可以將基站置于網絡中任一節點處，并從該節點開始分布式算法，發送角色消息的同時在消息內包括從開始節點計算的跳數，從而可以不付出額外的通信代價建立起任意節點到開始節點的最短路徑路由。各個DOMINATOR節點可以在確定自己的角色后通過多跳路由將位置信息傳遞回基站。此時，就可以將路徑優化問題轉換成旅行商問題，尋找一條最短的圈且經過每個點僅一次。然而，旅行商問題也被證明為NPhard問題。本文中使用kahng等提出的一種近似算法。該算法使用兩次連續的匹配來選擇完全圖中的一部分邊來將所有必須訪問的位置連接起來。第一次匹配選擇具有最小權重(本文中使用歐氏距離作為權重)的邊，是每個位置僅與一條邊相關聯。在將這些邊從圖中清除后再進行第二次匹配。兩次匹配所選擇的邊構成多個圈。然后。再將這些圈連接成一個大圈，即為算法的結果。在下一節中，我們將給出基于上述算法的仿真結果。

3 仿真評估

本節中，我們提供了支配集構建和路徑優化的仿真結果，并將本文的方法和基于樹形結構的收集方法的負載分布也通過仿真進行了比較。在仿真設置中，選擇了500×500單位長度的正方形區域作為傳感器網絡的部署區域。假定傳感器的傳輸范圍是圓形區域，通信半徑為r=50。

使用支配集的勢和所需使用的消息總數作為指標，首先將2．2節中的算法與Wan等提出的算法進行了比較。在基本場景中，我們使用1000個隨機分布的節點。通過改變節點數量使其從500變化到2000，模擬節點密度的變化。在每個場景下，我們進行10次仿真并取平均值作為實驗結果。實驗結果如圖4所示。在圖4(a)中，我們提出的算法所生成支配集的勢比較穩定，而Wan等所提出算法的結果則隨著節點數目的增加而略有增加。我們的結果具有更小的勢，僅為Wan等結果的50％～60％。在圖4(b)中，兩種算法的通信消耗都隨著節點數的增加而線性增長。我們的算法僅需要約占Wan等提出算法的50％的代價。我們的算法在支配集的勢和通信消耗兩個方面都優于Wan等提出的算法。隨后，分別基于上文中兩種算法的結果，使用kahng等提出的算法生成移動路徑。同樣改變節點數量從500到2000。在每個場景下，進行1O次仿真，并使用平均值進行比較。仿真結果如圖5所示。兩條曲線都隨著節點數的變化而波動，其原因是拓撲結構是隨機生成的，各個拓撲可能有不同的性質。但使用我們算法的結果要優于使用Wan等所提出算法的結果，即減少支配集的勢確實有助于縮短移動路徑的長度。

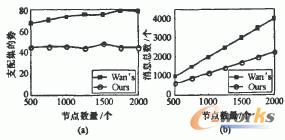
圖4支配集的勢和通信代價比較

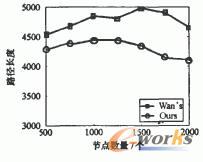
圖5 移動路徑的長度

我們分別對本文的方法與使用樹形結構且靜態基站位于網絡中心的方法進行了仿真。仿真使用了具有2500個節點的網格拓撲。兩種方案都需要構建最短路徑樹作為路由。此處我們忽略了構建最短路徑樹的通信消耗，而只考慮數據收集過程中的消耗。圖6顯示了我們提出的方案和基于樹形結構收集方案在一次性收集所有節點上數據時的負載分布。其中X、y分別表示二維平面的坐標軸，使用基于樹形結構的收集方法時，基站位于網絡的中心位置。很容易看出我們的方案僅有極低的通信消耗且具有更均衡的負載分布。在圖6(a)中，所有節點所需發送的消息數都不超過5，而在圖6(b)中相當一部分節點需要發送超過100個消息。在圖6(b)靠近中心位置處，有的節點需要發送的消息個數遠遠超出其他節點。正是這些節點的壽命限制了網絡壽命。仿真結果顯示我們的方案具有很好的可行性。與基于樹形結構的收集方法相比，它具有低通信消耗和更平衡的負載分布。我們的方案不需要轉發別的節點生成的數據，因此明顯比其他聯合使用移動基站和多跳路由方法更高效。

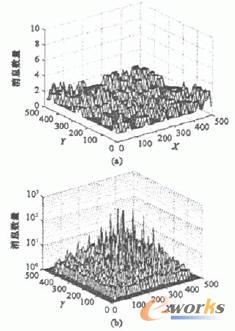
圖6 本文提出的方法和基于樹形結構收集的負載分布

4 小結

我們提出了一種基于移動基站而不使用多跳路由的數據收集方法。該方法結合了支配集相逢算法和旅行商問題的近似算法。仿真結果顯示，所提出的支配集構造算法具有更低的通信消耗和更低勢的支配集結果，并能生成更短的移動路徑。所提出的數據收集方法還具有負載均衡分布的特性。此外，該方法不使用UDG等理想狀態模型。從而具有很好的實用性。