控制系統的穩定性標準的相關知識

圖3中顯示了經典補償的典型環路增益曲線，其中顯示交越頻率為6.5 kHz。在此點，T(s)相位為-90°。如果您想在6.5 kHz時從-180°起步，并正向清點相位度數直至穿越幅角波形，您在此例中就得到90°的相位余量。這就是一個極為強健的系統，被認為在各種條件下都穩定：即使在交越點附近環路增益有一定程度的變化，也沒有可能在相位余量太小的頻率交越。所謂的“太小”，我們指的是相位余量接近30°極限，低于此值時系統就提供不可接受的振鈴(ringing)響應。這就是為什么您在上學時學習到45°是極限，此值相較于30°而言提供了額外的余量。我們稍后會看到這些數字的來源分析。

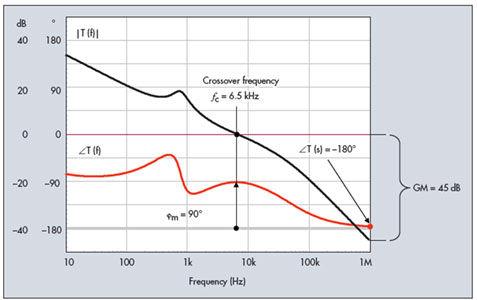
圖3. 在此示例中，0 dB交越點位于6.5 kHz，此頻率時總相位滯后提供了90°的相位余量

增益余量及穩定條件

圖4顯示了被補償轉換器的另一個典型頻率響應，重點顯示了0 dB交越點及相位余量。我們根據經驗可知，構成轉換器的元件在產生生命周期內會再現性能變化。這些變化可能是因正常的生產差異范圍引起的(如電阻或電容遭受逐批次公差不同的影響)。轉換器的環境工作條件也對元件有影響。在這些變量中，溫度充當關鍵角色，影響被動或主動元件參數，如電容或電感等效串列電阻(ESR)、光耦電流傳遞比(CTR)或是雙極晶體管的beta值。這些變量影響環路增益，使其上升或下降，具體則取決于受影響的參數。

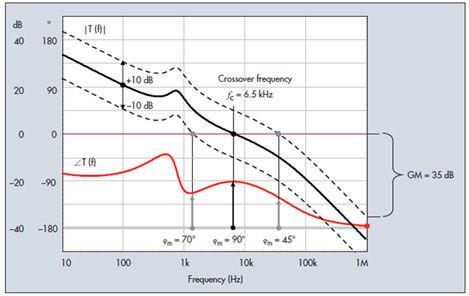
圖4. 環路增益會顯示出對溫度等外部參數的敏感性。出現變化時，相位余量必須始終保持在安全限制范圍內。

如果增益曲線出現變化，0 dB交越頻率將過渡至新的值，為轉換器施加不同的帶寬。在這些變化條件下轉換器的穩定性會受到怎樣的影響？如果新的交越頻率出現在相位余量較少的點，瞬時響應性能可能下降，使過沖不再能被接受。因此，身為設計人員，你的責任就是確保這些差量(dispersion)在你接近-180°極限時不會突然增大增益。您需要充足的增益余量，其定義如下所示：

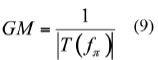
它對應于恰好為-180°或弧度的頻率點(圖3中為1 MHz)。

圖4描繪了由于所選擇元件生產差異范圍導致的±10 dB典型增益變化。它帶來了1.5 kHz至30 kHz的交越頻率。在此區域，相位余量從70°變為45°，這些都是理論上的安全數字。最壞情況是什么？就是新的交越頻率在總相位滯后180°處出現。這條件在1 MHz時出來，表示有35 dB的正增益變化。

不太可能有大增益

有利的是，當今電子電路中不太可能出現35 dB的增益變化。以前，在變壓器或伺服系統(servomechanism)采用真空管電路驅動的時候，上電序列期間的準備(warm-up)時間可能引起大的環路增益變化。因此，增益規定有必要排斥可能存在穩定性風險的第二個點。此總相位滯后達-180°的頻率處的環路增益曲線上可見這增益余量，在圖3中被標記為GM。在當今電子電路中，高于10 dB的增益余量通常就足夠了，除非您的環路增益對外部參數極為敏感。

增益漂移的另一個示例如圖5所示。圖中顯示另一個被補償的轉換器在10 kHz時出現80°的相位余量。根據前文的討論，我們知道可能會出現增益變化，致使增益曲線上揚或下走。在我們的示例中，我們可以發現2 kHz附近一個區域的相位余量小到只有18°。如果出現20至25 dB的增益下降，你最后得到的控制系統就會出現相當危險的約2 kHz的低相位余量。這就會導致振蕩響應，很可能超出過沖規范。此類系統被認為是有條件穩定。有利的是，如前所述，25 dB的增益變化并不常見，有這等增益余量的系統可被視為強健。然而，我看見過在一些設計案例中，最終使用者(您的客戶)在規范中清晰標明不接受有條件的設計，要求在低于交越頻率的所有點提供大于60°的相位余量。在這種情況下，就強制要求補償轉換器，使得無論什么工作條件下，低于交越頻率時都不存在相位余量降低的區域。

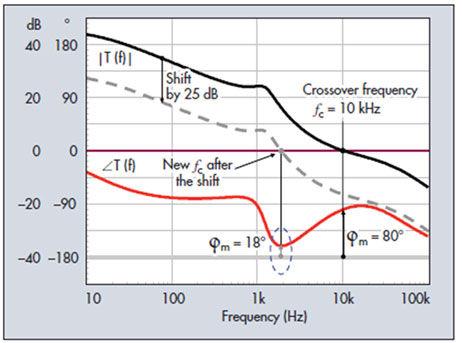
圖5. 在此示例中，如果增益漂移至低于25 dB，曲線就在相位余量僅為18°的頻率點過0 dB軸。如此的相位余量將受大的過問影響，提供振蕩極大的響應。這就是有條件穩定的案例。

穩定，或是不穩定？

通常認為，在交越前相位下降至低于-180°的系統是不穩定的系統。這樣的響應如圖6所示。在1 kHz后相位曲線快速下降，并在1.5 kHz之后的數kHz范圍內越過-180°的極限。然后相位曲線又上揚，在10 kHz時提供50°的相位余量。是的，此系統很穩定，只不過是因為在0 dB時我們不滿足方程式(7)。要記住的是，要消除方程式(3)的分母，您必須使增益大小恰好等于1且相位滯后180°或更多。在圖中，我們可以看到任何點都不滿足此條件。然而，值得一提的是，此環路極具條件相關性。如果增益減少數dB，您的相位余量將變得低于45°。增益再下降10 dB，您將進入相位余量為0的危險區，這時會達到振蕩條件。

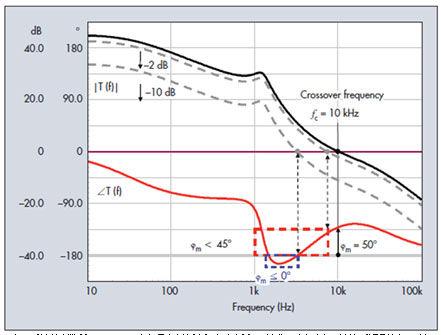
圖6. 相位滯后180°，但處于增益大于的區域。這并不構成問題，其回應可以接受